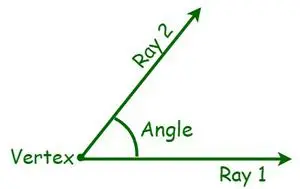
In der Geometrie ist ein Winkel ein wesentliches Maß einer geometrischen Form. Ein Winkel ist definiert als der Grad der Drehung um den Schnittpunkt zwischen zwei Linien oder Ebenen, der erforderlich ist, um die eine mit der anderen in Übereinstimmung zu bringen. Basierend auf der Messung eines Winkels gibt es verschiedene Arten von Winkeln. Sie wird in Grad oder Bogenmaß gemessen. Ein Winkel ist eine Form, die aus zwei Linien oder Strahlen besteht, die von einem gemeinsamen Punkt, einem sogenannten Scheitelpunkt, abweichen. Beim Schnittpunkt zweier Strahlen, also bei der Projektion von Halblinien mit einem gemeinsamen Endpunkt, entsteht ein Winkel. Nun werden die gemeinsamen Endpunkte als Scheitelpunkte bezeichnet, während die Strahlen als Arme bezeichnet werden.
Arten von Winkeln

- Spitzer Winkel: Ein spitzer Winkel ist ein Winkel, der größer als 0 Grad und kleiner als 90 Grad ist, d. h. er reicht von 0° bis 90° (beide ausschließlich).
- Rechter Winkel: Als rechter Winkel bezeichnet man den Winkel, der genau 90 Grad misst.
- Stumpfer Winkel: Ein stumpfer Winkel ist ein Winkel, der größer als 90 Grad und kleiner als 180 Grad ist, d. h. er reicht von 90° bis 180° (beide ausschließlich).
- Geraden Winkel: Als gerader Winkel wird ein Winkel bezeichnet, der genau 180 Grad misst.
- Überstumpfer Winkel: Ein Reflexwinkel ist ein Winkel, der größer als 180 Grad und kleiner als 360 Grad ist, d. h. er reicht von 180° bis 360° (beide ausschließlich).
- Ein vollständiger Winkel oder eine vollständige Drehung: Als vollständiger Winkel wird der Winkel bezeichnet, der genau 360 Grad misst.
Es gibt auch andere Arten von Winkeln, wie z. B. Komplementärwinkel, Ergänzungswinkel sowie benachbarte und nicht benachbarte Winkel.
- Ergänzende Winkel: Zwei Winkel heißen komplementär, wenn ihre Summe ein rechter Winkel, also 90°, ist.
- Ergänzungswinkel: Zwei Winkel heißen komplementär, wenn ihre Summe 180° beträgt.
- Angrenzende Winkel: Zwei Winkel heißen benachbart, wenn sie einen gemeinsamen Scheitelpunkt und einen gemeinsamen Arm haben.
- Nicht benachbarte Winkel: Zwei Winkel heißen nicht benachbart, wenn sie keinen gemeinsamen Scheitelpunkt und keinen gemeinsamen Arm haben.
Die Formel zum Finden von Winkeln
Es gibt verschiedene Arten von Formeln zum Ermitteln eines Winkels. Einige davon sind die Zentralwinkelformel, die Doppelwinkelformel, die Halbwinkelformel, die zusammengesetzte Winkelformel, die Innenwinkelformel usw.
- Wir verwenden die Zentriwinkelformel, um den Winkel eines Kreissegments zu bestimmen.
- Wir verwenden die Formel für die Summe der Innenwinkel, um den fehlenden Winkel in einem Polygon zu bestimmen.
- Wir verwenden die trigonometrischen Verhältnisse, um den fehlenden Winkel eines rechtwinkligen Dreiecks zu ermitteln.
- Wir verwenden das Sinusgesetz oder das Kosinusgesetz, um den fehlenden Winkel eines nicht rechtwinkligen Dreiecks zu ermitteln.
Name der Formel | Formel | Wie finde ich einen unbekannten Winkel? |
|---|---|---|
| Mittelwinkelformel | θ =(s × 360°)/2prDabei ist s die Bogenlänge und r der Radius des Kreises | Ersetzen Sie die Werte der Bogenlänge und des Kreisradius, um den Winkel eines in einem Kreis gebildeten Segments zu bestimmen. |
| Formel für die Summe der Innenwinkel | 180°(n-2)Hier ist n die Anzahl der Seiten eines Polygons | Um den unbekannten Innenwinkel eines Polygons zu bestimmen, berechnen Sie zunächst die Summe aller Innenwinkel mit dieser Formel und subtrahieren dann die Summe aller bekannten Winkel vom Ergebnis. |
| Trigonometrische Verhältnisse | sin θ = opposite side/hypotenusecos θ = Ankathete/Hypotenusetan θ = gegenüberliegende Seite/angrenzende Seite | Wählen Sie abhängig von den verfügbaren zwei Seiten eines rechtwinkligen Dreiecks eines dieser trigonometrischen Verhältnisse, um den unbekannten Winkel zu ermitteln. |
| Sinusgesetz | a/sin A = b/sin B = c/sin CDabei sind A, B und C die Innenwinkel eines Dreiecks und a, b und c die jeweiligen gegenüberliegenden Seiten. | Wenn wir zwei Seiten und einen nicht eingeschlossenen Winkel kennen (oder) zwei Winkel und eine nicht eingeschlossene Seite, dann kann das Sinusgesetz verwendet werden, um die unbekannten Winkel eines Dreiecks zu bestimmen. |
| Kosinusgesetz | A2= b2+ c2– 2vc cos AB2= c2+ a2– 2ca cos BC2= a2+ b2– 2ab cos CDabei sind A, B und C die Innenwinkel eines Dreiecks und a, b und c die jeweiligen gegenüberliegenden Seiten. | Wenn wir drei Seiten (oder) zwei Seiten und einen eingeschlossenen Winkel kennen, kann das Kosinusgesetz verwendet werden, um die unbekannten Winkel eines Dreiecks zu bestimmen. |
Probefragen
Frage 1: Ermitteln Sie den Winkel am Scheitelpunkt B des gegebenen Dreiecks mithilfe einer der trigonometrischen Formeln zum Ermitteln von Winkeln.

Lösung:
Gegeben,
BC = 3 Einheiten = Angrenzende Seite von θ.
AC = 4 Einheiten = Gegenseite von θ.
In diesem Fall kennen wir sowohl die gegenüberliegende als auch die benachbarte Seite von θ. Daher können wir die Tangensformel verwenden, um θ zu finden.
⇒ tan θ = gegenüberliegende Seite/angrenzende Seite
⇒ tan θ = 4/3
⇒ θ = tan-1(4/3) ⇒ θ = 53,1°
Daher beträgt der Winkel am Scheitelpunkt B 53,1°.
Frage 2: Finden Sie die Winkel an den Eckpunkten X und Y, wenn ∠Z = 35° und x = 3 Zoll, y = 8 Zoll und z = 3,5 Zoll.

Lösung:
Gegeben,
∠Z = 35° und x = 6 Zoll, y = 3 Zoll und z = 3,5 Zoll
Da wir alle drei Seiten und einen Winkel kennen, können wir die Sinusregelformel verwenden.
Aus der Sinusregelformel ergibt sich:
x/sin X = y/sin Y = z/sin Z
Jetzt,
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/ohne Y = 3,5/0,574 {Da sin 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = Sünde−1(0,492) = 29,47°
Wir wissen, dass die Summe dreier Winkel in einem Dreieck 180° beträgt.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Daher ist ∠X = 115,53° und ∠Y = 29,47°.
Frage 3: Berechnen Sie den fünften Innenwinkel eines Fünfecks, wenn vier seiner Innenwinkel 110°, 85°, 136° und 105° betragen.
Lösung:
Die Anzahl der Seiten eines Fünfecks (n) = 5.
Nun ist die Summe aller 5 Innenwinkel eines Fünfecks = 180 (n -2)°
= 180 (5 – 2)° = 540°.
Die Summe der gegebenen 4 Innenwinkel = 110°+ 85°+ 136°+ und 105°= 436°.
Der fünfte Innenwinkel = 540° – 436° = 104°
Somit beträgt der fünfte Innenwinkel eines Fünfecks 104°.
Frage 4: Bestimmen Sie den Wert von y und auch das Winkelmaß in der gegebenen Figur.

Lösung:
Aus der angegebenen Abbildung können wir erkennen, dass (4y – 6)° und (3y + 5)° komplementäre Winkel sind, d. h. die Summe von (4y – 6)° und (3y + 5)° beträgt 90 °.
⇒ (4J – 6)° + (3J + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Nun ist (4y – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Frage 5: Ermitteln Sie den Winkel am Scheitelpunkt Q im gegebenen Dreieck mithilfe einer der Formeln zum Ermitteln von Winkeln.

Lösung:
Gegeben sei p = QR = 6 cm, q = PR = 9 cm und r = PQ = 7 cm.
Da wir alle drei Seiten und einen Winkel kennen, können wir die Kosinusregelformel verwenden, um den Winkelscheitelpunkt Q zu ermitteln.
⇒ q2= S2+ r2– 2 pro Person, weil Q
⇒ 92= 62+ 72– 2 (6)(7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
lang zum BespannenDaher beträgt der Winkel am Scheitelpunkt Q ∠Q = 92,72°.
Frage 6: Berechnen Sie den Winkel eines Kreissegments, wenn die Bogenlänge 12π und der Radius 9 cm beträgt.
Lösung:
Gegeben,
Die Bogenlänge = 12π
Radius (r) = 9 cm
Die Winkelformel lautet nun:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
Daher beträgt der Winkel 240°.
