Z-SCORE IN DER STATISTIK - DATENWISSENSCHAFT

Z-Score in der Statistik ist ein Maß dafür, wie viele Standardabweichungen ein Datenpunkt vom Mittelwert einer Verteilung hat. Lassen Sie uns den Z-Score in der Statistik ermitteln. Ein Z-Score von 0 gibt an, dass der Score des Datenpunkts mit dem Mittelwert übereinstimmt. Ein positiver Z-Score zeigt an, dass der Datenpunkt über dem Durchschnitt liegt, während ein negativer Z-Score anzeigt, dass der Datenpunkt unter dem Durchschnitt liegt.

Die Formel zur Berechnung eines Z-Scores lautet: z = (x – μ)/ p

Wo:

X: ist der Testwert
M: ist der Mittelwert
bei: ist der Standardwert

In diesem Artikel werden wir die folgenden Konzepte diskutieren:

Inhaltsverzeichnis

Was ist Z-Score?
Wie berechnet man den Z-Score?
Eigenschaften des Z-Scores
Berechnen Sie Ausreißer mithilfe des Z-Score-Werts
Implementierung von Z-Score in Python
Anwendung des Z-Scores
Z-Scores vs. Standardabweichung
Warum werden Z-Scores als Standard-Scores bezeichnet?

Was ist Z-Score?

Der Z-Score, auch Standard-Score genannt, gibt Auskunft über die Abweichung eines Datenpunkts vom Mittelwert, indem er ihn in Standardabweichungen über oder unter dem Mittelwert ausdrückt. Es gibt uns eine Vorstellung davon, wie weit ein Datenpunkt vom Mittelwert entfernt ist. Daher wird der Z-Score anhand der Standardabweichung vom Mittelwert gemessen. Ein Z-Score von 2 bedeutet beispielsweise, dass der Wert 2 Standardabweichungen vom Mittelwert entfernt ist. Um einen Z-Score zu verwenden, müssen wir den Populationsmittelwert (μ) und auch die Populationsstandardabweichung (σ) kennen.

Die Formel für den Z-Score

Ein Z-Score kann mit der folgenden Formel berechnet werden.

z = (X – μ) / p

Wo,

z = Z-Score
X = Wert des Elements
μ = Bevölkerungsmittelwert
σ = Population Standard Deviation

Wie berechnet man den Z-Score?

Wir erhalten den Populationsmittelwert (μ), die Populationsstandardabweichung (σ) und den beobachteten Wert (x) in der Problemstellung. Wenn wir diesen in die Z-Score-Gleichung einsetzen, erhalten wir den Z-Score-Wert. Abhängig davon, ob der angegebene Z-Score positiv oder negativ ist, können wir verwenden positive Z-Tabelle oder negativer Z-Tisch Verfügbar online oder auf der Rückseite Ihres Statistiklehrbuchs im Anhang.

Beispiel 1:

Sie nehmen an der GATE-Prüfung teil und erzielen eine Punktzahl von 500. Die durchschnittliche Punktzahl für die GATE-Prüfung liegt bei 390 und die Standardabweichung bei 45. Wie gut haben Sie im Test im Vergleich zum durchschnittlichen Testteilnehmer abgeschnitten?

Lösung:

Die folgenden Daten sind in der obigen Fragestellung leicht verfügbar

Rohwert/beobachteter Wert = X = 500

Mittlere Punktzahl = μ = 390

Standard deviation = σ = 45

Durch Anwendung der Formel des Z-Scores

z = (X – μ) / p

z = (500 – 390) / 45

z = 110 / 45 = 2,44

Das bedeutet, dass Ihr Z-Score ist 2.44 .

Da der Z-Score positiv 2,44 ist, verwenden wir die positive Z-Tabelle.

Werfen wir nun einen Blick darauf Z-Tisch (CC-BY), um zu erfahren, wie gut Sie im Vergleich zu den anderen Testteilnehmern abgeschnitten haben.

Befolgen Sie die nachstehenden Anweisungen, um die Wahrscheinlichkeit aus der Tabelle zu ermitteln.

Hier, Z-Score = 2,44, welche ich Zeigt an, dass der Datenpunkt 2,44 Standardabweichungen über dem Mittelwert liegt.

Ordnen Sie zunächst die ersten beiden Ziffern 2,4 auf der Y-Achse zu.
Zeichnen Sie dann entlang der X-Achse 0,04 ab
Verbinden Sie beide Achsen. Der Schnittpunkt der beiden liefert Ihnen die kumulative Wahrscheinlichkeit, die mit dem gesuchten Z-Score-Wert verbunden ist

[Diese Wahrscheinlichkeit stellt die Fläche unter der Standardnormalkurve links vom Z-Score dar]

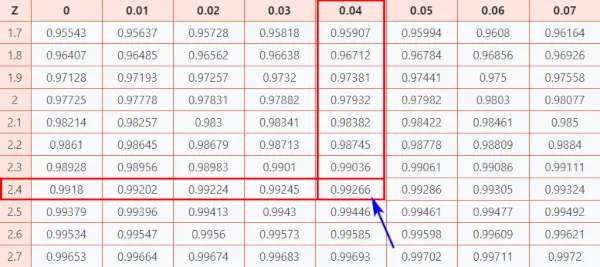
Normalverteilungstabelle

Als Ergebnis erhalten Sie den Endwert 0,99266 .

Jetzt müssen wir vergleichen, wie unsere ursprüngliche Punktzahl von 500 bei der GATE-Prüfung mit der durchschnittlichen Punktzahl der Gruppe verglichen wird. Dazu müssen wir die mit dem Z-Score verbundene kumulative Wahrscheinlichkeit in einen Prozentwert umwandeln.

0,99266 × 100 = 99,266 %

Abschließend kann man sagen, dass Sie eine gute Leistung erbracht haben 99 % anderer Testteilnehmer.

Beispiel 2 : Wie groß ist die Wahrscheinlichkeit, dass ein Schüler eine Punktzahl zwischen 350 und 400 erreicht (bei einer mittleren Punktzahl μ von 390 und einer Standardabweichung σ von 45)?

Lösung:

Mindestpunktzahl = X₁= 350

Maximale Punktzahl = X₂= 400

Durch Anwendung der Formel des Z-Scores

Mit₁= (X1 – m) / p

Mit₁= (350 – 390) / 45

Mit₁= -40 / 45 = -0,88

Mit₂= (X₂– m) / p

z2 = (400 – 390) / 45

Mit₂= 10 / 45 = 0,22

Da z1 negativ ist, müssen wir uns ein Negativ ansehen Z-Tisch und finden Sie heraus, dass die kumulative Wahrscheinlichkeit p1, die erste Wahrscheinlichkeit, ist 0,18943 .

Mit₂positiv ist, daher verwenden wir eine positive Z-Tabelle, die eine kumulative Wahrscheinlichkeit p ergibt₂von 0,58706 .

Die endgültige Wahrscheinlichkeit wird durch Subtrahieren von p1 von p berechnet₂:

p = p₂- P₁

p = 0,58706 – 0,18943 = 0,39763

Die Wahrscheinlichkeit, dass ein Schüler eine Punktzahl zwischen 350 und 400 erreicht, beträgt 39,763 % (0,39763 * 100).

Eigenschaften des Z-Scores

Die Größe des Z-Scores spiegelt wider, wie weit ein Datenpunkt hinsichtlich der Standardabweichungen vom Mittelwert entfernt ist.
Ein Element mit einem Z-Score von weniger als 0 bedeutet, dass das Element kleiner als der Mittelwert ist.
Z-Scores ermöglichen den Vergleich von Datenpunkten aus verschiedenen Verteilungen.
Ein Element mit einem Z-Score größer als 0 bedeutet, dass das Element größer als der Mittelwert ist.
Ein Element mit einem Z-Score von 0 bedeutet, dass das Element gleich dem Mittelwert ist.
Ein Element mit einem Z-Score von 1 bedeutet, dass das Element um 1 Standardabweichung größer als der Mittelwert ist. ein Z-Score von 2, 2 Standardabweichungen größer als der Mittelwert usw.
Ein Element mit einem Z-Score von -1 bedeutet, dass das Element um 1 Standardabweichung kleiner als der Mittelwert ist. ein Z-Score von -2, 2 Standardabweichungen kleiner als der Mittelwert usw.
Wenn die Anzahl der Elemente in einer bestimmten Menge groß ist, haben etwa 68 % der Elemente einen Z-Score zwischen -1 und 1; etwa 95 % haben einen Z-Score zwischen -2 und 2; etwa 99 % haben einen Z-Score zwischen -3 und 3. Dies wird als empirische Regel bezeichnet und gibt den Prozentsatz der Daten innerhalb bestimmter Standardabweichungen vom Mittelwert in einer Normalverteilung an, wie im Bild unten dargestellt

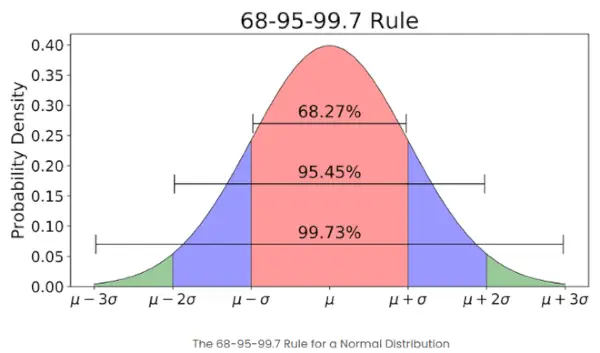
Die empirische Regel in der Normalverteilung

Berechnen Sie Ausreißer mithilfe des Z-Score-Werts

Ausreißer in den Daten können wir anhand des Z-Score-Werts der Datenpunkte berechnen. Die Schritte zur Berücksichtigung eines Ausreißer-Datenpunkts sind wie folgt:

Zunächst erfassen wir den Datensatz, in dem wir die Ausreißer sehen möchten
Wir berechnen den Mittelwert und die Standardabweichung des Datensatzes. Diese Werte werden zur Berechnung des Z-Score-Werts jedes Datenpunkts verwendet.
Wir berechnen den Z-Score-Wert für jeden Datenpunkt. Die Formel zur Berechnung des Z-Score-Werts ist dieselbe wie
Z = frac{{X – mu}}{{sigma}}
Dabei ist X der Datenpunkt, μ der Mittelwert der Daten und σ die Standardabweichung des Datensatzes.
Wir werden den Grenzwert für den Z-Score bestimmen, nach dem der Datenpunkt als Ausreißer betrachtet werden könnte. Dieser Grenzwert ist ein Hyperparameter, den wir je nach Projekt festlegen.
Ein Datenpunkt, dessen Z-Score-Wert größer als 3 ist, bedeutet, dass der Datenpunkt nicht zum 99,73 %-Punkt des Datensatzes gehört.
Jeder Datenpunkt, dessen Z-Score größer als unser festgelegter Grenzwert ist, wird als Ausreißer betrachtet.

Überprüfen: Z-Score für Ausreißererkennung

Implementierung von Z-Score in Python

Wir können Python verwenden, um den Z-Score-Wert von Datenpunkten im Datensatz zu berechnen. Außerdem werden wir die Numpy-Bibliothek verwenden, um den Mittelwert und die Standardabweichung des Datensatzes zu berechnen.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Die Ausreißer im Datensatz sind {Ausreißer}')>

Ausgabe:

Z-Score: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Die Ausreißer im Datensatz sind [150]

Anwendung des Z-Scores

Z-Scores werden häufig zur Feature-Skalierung verwendet, um verschiedene Features auf einen gemeinsamen Maßstab zu bringen. Durch die Normalisierung von Merkmalen wird sichergestellt, dass sie einen Mittelwert und eine Einheitsvarianz von Null aufweisen, was für bestimmte Algorithmen für maschinelles Lernen von Vorteil sein kann, insbesondere für solche, die auf Distanzmaßen basieren.
Z-Scores können verwendet werden, um Ausreißer in einem Datensatz zu identifizieren. Datenpunkte mit Z-Scores über einem bestimmten Schwellenwert (normalerweise 3 Standardabweichungen vom Mittelwert) können als Ausreißer betrachtet werden.
Z-Scores können in Algorithmen zur Anomalieerkennung verwendet werden, um Fälle zu identifizieren, die erheblich vom erwarteten Verhalten abweichen.
Z-Scores können angewendet werden, um schiefe Verteilungen in eher normale Verteilungen umzuwandeln.
Bei der Arbeit mit Regressionsmodellen können Z-Scores von Residuen analysiert werden, um auf Homoskedastizität (konstante Varianz der Residuen) zu prüfen.
Z-Scores können bei der Feature-Skalierung verwendet werden, indem ihre Standardabweichungen vom Mittelwert betrachtet werden.

Z-Scores vs. Standardabweichung

Z-Score	Standardabweichung
Rohdaten in eine standardisierte Skala umwandeln.	Misst das Ausmaß der Variation oder Streuung in einer Reihe von Werten.
Erleichtert den Vergleich von Werten aus verschiedenen Datensätzen, da die ursprünglichen Maßeinheiten entfernt werden.	Die Standardabweichung behält die ursprünglichen Maßeinheiten bei und eignet sich daher weniger für direkte Vergleiche zwischen Datensätzen mit unterschiedlichen Einheiten.
Geben Sie an, wie weit ein Datenpunkt in Bezug auf Standardabweichungen vom Mittelwert entfernt ist, und geben Sie so ein Maß für die relative Position des Datenpunkts innerhalb der Verteilung an	Wird in denselben Einheiten wie die Originaldaten ausgedrückt und bietet ein absolutes Maß dafür, wie weit die Werte um den Mittelwert verteilt sind

Überprüfen: Z-Score-Tabelle

Warum werden Z-Scores als Standard-Scores bezeichnet?

Z-Scores werden auch als Standard-Scores bezeichnet, da sie den Wert einer Zufallsvariablen standardisieren. Das bedeutet, dass die Liste der standardisierten Scores einen Mittelwert von 0 und eine Standardabweichung von 1,0 aufweist. Z-Scores ermöglichen auch den Vergleich von Scores für verschiedene Arten von Variablen. Dies liegt daran, dass sie den relativen Rang verwenden, um Ergebnisse verschiedener Variablen oder Verteilungen gleichzusetzen.

Z-Scores werden häufig verwendet, um eine Variable mit einer Standardnormalverteilung (mit μ = 0 und σ = 1) zu vergleichen.

Letztes Zeichen aus der Zeichenfolge entfernen

Z-Score in der Statistik – FAQs

Welche Bedeutung haben positive und negative Z-Scores?

Positive Z-Scores geben Werte über dem Mittelwert an, während negative Z-Scores Werte unter dem Mittelwert anzeigen. Das Vorzeichen gibt die Richtung der Abweichung vom Mittelwert wieder.

Was bedeutet ein Z-Score von 0?

Ein Z-Score von 0 gibt an, dass der Wert des Datenpunkts genau dem Mittelwert des Datensatzes entspricht. Dies deutet darauf hin, dass der Datenpunkt weder über noch unter dem Mittelwert liegt.

Was ist die 68-95-99,7-Regel in Bezug auf Z-Scores?

Die 68-95-99,7-Regel, auch empirische Regel genannt, besagt:

Etwa 68 % der Daten liegen innerhalb einer Standardabweichung vom Mittelwert.
Etwa 95 % liegen innerhalb von 2 Standardabweichungen.
Etwa 99,7 % liegen innerhalb von 3 Standardabweichungen.

Können Z-Scores für Nichtnormalverteilungen verwendet werden?

Z-Scores basieren auf der Annahme, dass die Daten einer Normalverteilung folgen. In der Praxis sind Z-Scores jedoch für Daten vorteilhaft, die einer Normalverteilung folgen. Während Z-Scores für jede Verteilung berechnet werden können, wird ihre Interpretation bei der Verarbeitung nicht normalverteilter Daten weniger zuverlässig und eindeutig.

Wie können Z-Scores in realen Situationen angewendet werden?

Z-Scores finden vielfältige Anwendungsmöglichkeiten, beispielsweise im Finanzbereich für Portfolioanalysen, im Bildungswesen für standardisierte Tests, im Gesundheitswesen für klinische Bewertungen und mehr. Sie bieten ein standardisiertes Maß für den Vergleich und die Interpretation von Daten.