Seit der Erfindung des Computers verwenden Menschen den Begriff „ Daten ', um sich auf Computerinformationen zu beziehen, die entweder übertragen oder gespeichert werden. Es gibt jedoch auch Daten, die in Auftragstypen vorhanden sind. Daten können auf ein Blatt Papier geschriebene Zahlen oder Texte sein, in Form von Bits und Bytes, die im Speicher elektronischer Geräte gespeichert sind, oder Fakten, die im Kopf einer Person gespeichert sind. Als sich die Welt zu modernisieren begann, wurden diese Daten zu einem wichtigen Aspekt des täglichen Lebens eines jeden Menschen, und verschiedene Implementierungen ermöglichten es ihnen, sie unterschiedlich zu speichern.

Daten ist eine Sammlung von Fakten und Zahlen oder eine Menge von Werten oder Werten eines bestimmten Formats, die sich auf eine einzelne Menge von Elementwerten bezieht. Die Datenelemente werden dann in Unterelemente klassifiziert. Dabei handelt es sich um die Gruppe von Elementen, die nicht als einfache Primärform des Elements bekannt sind.

Betrachten wir ein Beispiel, bei dem der Name eines Mitarbeiters in drei Unterelemente unterteilt werden kann: „Vorname“, „Mittelname“ und „Nachname“. Eine einem Mitarbeiter zugewiesene ID wird jedoch im Allgemeinen als ein einzelnes Element betrachtet.

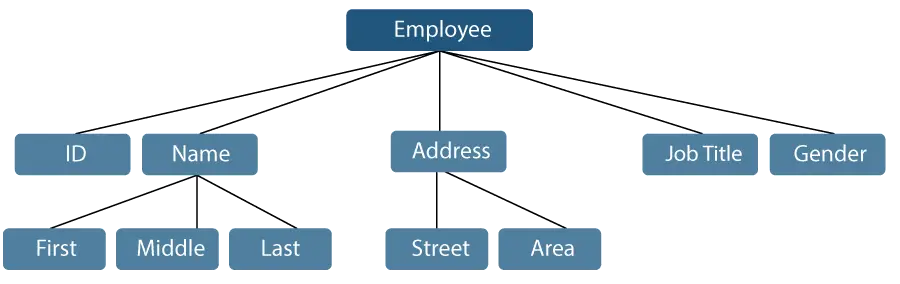
Abbildung 1: Darstellung von Datenelementen

Im oben genannten Beispiel sind die Elemente wie ID, Alter, Geschlecht, Vorname, Mitte, Nachname, Straße, Ort usw. elementare Datenelemente. Im Gegensatz dazu sind der Name und die Adresse Gruppendatenelemente.

Was ist Datenstruktur?

Datenstruktur ist ein Teilgebiet der Informatik. Das Studium der Datenstruktur ermöglicht es uns, die Organisation von Daten und die Verwaltung des Datenflusses zu verstehen, um die Effizienz jedes Prozesses oder Programms zu steigern. Datenstruktur ist eine besondere Methode zum Speichern und Organisieren von Daten im Speicher des Computers, sodass diese Daten bei Bedarf in Zukunft leicht abgerufen und effizient genutzt werden können. Die Daten können auf verschiedene Arten verwaltet werden, so wird das logische oder mathematische Modell für eine bestimmte Datenorganisation als Datenstruktur bezeichnet.

Der Umfang eines bestimmten Datenmodells hängt von zwei Faktoren ab:

1. Erstens muss es ausreichend in die Struktur geladen werden, um die eindeutige Korrelation der Daten mit einem realen Objekt widerzuspiegeln.
2. Zweitens sollte die Bildung so einfach sein, dass man sie bei Bedarf anpassen kann, um die Daten effizient zu verarbeiten.

Einige Beispiele für Datenstrukturen sind Arrays, verknüpfte Listen, Stapel, Warteschlangen, Bäume usw. Datenstrukturen werden in fast allen Aspekten der Informatik häufig verwendet, d. h. Compiler-Design, Betriebssysteme, Grafik, künstliche Intelligenz und viele mehr.

Datenstrukturen sind der Hauptbestandteil vieler Informatikalgorithmen, da sie es den Programmierern ermöglichen, die Daten effektiv zu verwalten. Es spielt eine entscheidende Rolle bei der Verbesserung der Leistung eines Programms oder einer Software, da das Hauptziel der Software darin besteht, die Daten des Benutzers so schnell wie möglich zu speichern und abzurufen.

Java Long zum Stringen

Grundlegende Terminologien im Zusammenhang mit Datenstrukturen

Datenstrukturen sind die Bausteine ​​jeder Software oder jedes Programms. Die Auswahl der geeigneten Datenstruktur für ein Programm ist für einen Programmierer eine äußerst anspruchsvolle Aufgabe.

Im Folgenden sind einige grundlegende Terminologien aufgeführt, die verwendet werden, wenn es um Datenstrukturen geht:

Daten:Wir können Daten als einen elementaren Wert oder eine Sammlung von Werten definieren. Beispielsweise sind der Name und die ID des Mitarbeiters die Daten, die sich auf den Mitarbeiter beziehen.Datenelemente:Eine einzelne Werteinheit wird als Datenelement bezeichnet.Gruppenelemente:Datenelemente, die über untergeordnete Datenelemente verfügen, werden als Gruppenelemente bezeichnet. Beispielsweise kann der Name eines Mitarbeiters einen Vor-, Zweit- und Nachnamen haben.Grundelemente:Datenelemente, die nicht in Unterelemente unterteilt werden können, werden als Elementarelemente bezeichnet. Zum Beispiel die ID eines Mitarbeiters.Entität und Attribut:Eine Klasse bestimmter Objekte wird durch eine Entität repräsentiert. Es besteht aus verschiedenen Attributen. Jedes Attribut symbolisiert die spezifische Eigenschaft dieser Entität. Zum Beispiel,

Entitäten mit ähnlichen Attributen bilden eine Entitätssatz . Jedes Attribut einer Entitätsmenge verfügt über einen Wertebereich, die Menge aller möglichen Werte, die dem spezifischen Attribut zugewiesen werden könnten.

Der Begriff „Informationen“ wird manchmal für Daten mit bestimmten Attributen bedeutungsvoller oder verarbeiteter Daten verwendet.

Feld:Eine einzelne elementare Informationseinheit, die das Attribut einer Entität symbolisiert, wird als Feld bezeichnet.Aufzeichnen:Eine Sammlung verschiedener Datenelemente wird als Datensatz bezeichnet. Wenn wir beispielsweise über die Entität „Mitarbeiter“ sprechen, können Name, ID, Adresse und Berufsbezeichnung gruppiert werden, um den Datensatz für den Mitarbeiter zu bilden.Datei:Eine Sammlung verschiedener Datensätze eines Entitätstyps wird als Datei bezeichnet. Wenn es beispielsweise 100 Mitarbeiter gibt, enthält die zugehörige Datei 25 Datensätze mit Daten zu jedem Mitarbeiter.

Den Bedarf an Datenstrukturen verstehen

Da Anwendungen immer komplexer werden und die Datenmenge täglich zunimmt, kann dies zu Problemen bei der Datensuche, der Verarbeitungsgeschwindigkeit, der Bearbeitung mehrerer Anfragen und vielem mehr führen. Datenstrukturen unterstützen verschiedene Methoden zum effizienten Organisieren, Verwalten und Speichern von Daten. Mit Hilfe von Datenstrukturen können wir die Datenelemente einfach durchlaufen. Datenstrukturen bieten Effizienz, Wiederverwendbarkeit und Abstraktion.

Warum sollten wir Datenstrukturen lernen?

1. Datenstrukturen und Algorithmen sind zwei der Schlüsselaspekte der Informatik.
2. Datenstrukturen ermöglichen es uns, Daten zu organisieren und zu speichern, während Algorithmen es uns ermöglichen, diese Daten sinnvoll zu verarbeiten.
3. Das Erlernen von Datenstrukturen und Algorithmen wird uns helfen, bessere Programmierer zu werden.
4. Wir werden in der Lage sein, Code zu schreiben, der effektiver und zuverlässiger ist.
5. Außerdem können wir Probleme schneller und effizienter lösen.

Die Ziele von Datenstrukturen verstehen

Datenstrukturen erfüllen zwei komplementäre Ziele:

Richtigkeit:Datenstrukturen sind so konzipiert, dass sie für alle Arten von Eingaben basierend auf der interessierenden Domäne korrekt funktionieren. Mit anderen Worten: Korrektheit bildet das Hauptziel der Datenstruktur, das immer von den Problemen abhängt, die die Datenstruktur lösen soll.Effizienz:Datenstrukturen müssen auch effizient sein. Es sollte die Daten schnell verarbeiten, ohne viele Computerressourcen wie Speicherplatz zu beanspruchen. Im Echtzeitzustand ist die Effizienz einer Datenstruktur ein Schlüsselfaktor für Erfolg und Misserfolg des Prozesses.

Einige Hauptmerkmale von Datenstrukturen verstehen

Einige der wesentlichen Merkmale von Datenstrukturen sind:

Robustheit:Im Allgemeinen ist es das Ziel aller Computerprogrammierer, Software zu erstellen, die für jede mögliche Eingabe eine korrekte Ausgabe liefert und auf allen Hardwareplattformen effizient ausgeführt wird. Diese Art robuster Software muss sowohl gültige als auch ungültige Eingaben verwalten.Anpassungsfähigkeit:Die Erstellung von Softwareanwendungen wie Webbrowsern, Textverarbeitungsprogrammen und Internetsuchmaschinen umfasst riesige Softwaresysteme, die über viele Jahre eine korrekte und effiziente Arbeit oder Ausführung erfordern. Darüber hinaus entwickelt sich Software aufgrund neuer Technologien oder sich ständig ändernder Marktbedingungen weiter.Wiederverwendbarkeit:Die Funktionen wie Wiederverwendbarkeit und Anpassungsfähigkeit gehen Hand in Hand. Es ist bekannt, dass der Programmierer viele Ressourcen benötigt, um Software zu erstellen, was es zu einem kostspieligen Unterfangen macht. Wenn die Software jedoch wiederverwendbar und anpassbar entwickelt wird, kann sie in den meisten zukünftigen Anwendungen eingesetzt werden. Somit ist es durch die Ausführung hochwertiger Datenstrukturen möglich, wiederverwendbare Software zu erstellen, die kosteneffektiv und zeitsparend erscheint.

Klassifizierung von Datenstrukturen

Eine Datenstruktur liefert einen strukturierten Satz von Variablen, die auf verschiedene Weise miteinander in Beziehung stehen. Es bildet die Grundlage eines Programmiertools, das die Beziehung zwischen den Datenelementen darstellt und es Programmierern ermöglicht, die Daten effizient zu verarbeiten.

Wir können Datenstrukturen in zwei Kategorien einteilen:

Hrithik Roshan Alter

1. Primitive Datenstruktur
2. Nicht-primitive Datenstruktur

Die folgende Abbildung zeigt die verschiedenen Klassifizierungen von Datenstrukturen.

Figur 2: Klassifikationen von Datenstrukturen

Primitive Datenstrukturen

Primitive Datenstrukturensind die Datenstrukturen bestehend aus den Zahlen und den kommenden Zeichen eingebaut in Programme umwandeln.
1. Diese Datenstrukturen können direkt durch Anweisungen auf Maschinenebene manipuliert oder betrieben werden.
2. Grundlegende Datentypen wie Ganzzahl, Gleitkomma, Zeichen , Und Boolescher Wert fallen unter die primitiven Datenstrukturen.
3. Diese Datentypen werden auch aufgerufen Einfache Datentypen , da sie Zeichen enthalten, die nicht weiter unterteilt werden können

Nicht-primitive Datenstrukturen

Nicht-primitive Datenstrukturensind Datenstrukturen, die von primitiven Datenstrukturen abgeleitet sind.
1. Diese Datenstrukturen können nicht direkt durch Anweisungen auf Maschinenebene manipuliert oder bedient werden.
2. Der Schwerpunkt dieser Datenstrukturen liegt auf der Bildung eines Satzes von Datenelementen, die beides sind homogen (gleicher Datentyp) oder heterogen (verschiedene Datentypen).
3. Basierend auf der Struktur und Anordnung der Daten können wir diese Datenstrukturen in zwei Unterkategorien einteilen:
   1. Lineare Datenstrukturen
   2. Nichtlineare Datenstrukturen

Lineare Datenstrukturen

Eine Datenstruktur, die eine lineare Verbindung zwischen ihren Datenelementen beibehält, wird als lineare Datenstruktur bezeichnet. Die Anordnung der Daten erfolgt linear, wobei jedes Element bis auf das erste und das letzte Datenelement aus den Nachfolgern und Vorgängern besteht. Dies gilt jedoch nicht unbedingt für den Speicher, da die Anordnung möglicherweise nicht sequentiell ist.

Basierend auf der Speicherzuordnung werden die linearen Datenstrukturen weiter in zwei Typen eingeteilt:

Statische Datenstrukturen:Die Datenstrukturen mit einer festen Größe werden als statische Datenstrukturen bezeichnet. Der Speicher für diese Datenstrukturen wird zum Zeitpunkt des Compilers zugewiesen und ihre Größe kann vom Benutzer nach der Kompilierung nicht geändert werden. die darin gespeicherten Daten können jedoch verändert werden.
Der Array ist das beste Beispiel für die statische Datenstruktur, da sie eine feste Größe haben und ihre Daten später geändert werden können.Dynamische Datenstrukturen:Die Datenstrukturen mit dynamischer Größe werden als dynamische Datenstrukturen bezeichnet. Der Speicher dieser Datenstrukturen wird zur Laufzeit zugewiesen und ihre Größe variiert während der Laufzeit des Codes. Darüber hinaus kann der Benutzer die Größe sowie die in diesen Datenstrukturen gespeicherten Datenelemente zur Laufzeit des Codes ändern.
Verknüpfte Listen, Stapel , Und Schwänze sind häufige Beispiele für dynamische Datenstrukturen

Arten linearer Datenstrukturen

Das Folgende ist die Liste der linearen Datenstrukturen, die wir im Allgemeinen verwenden:

1. Arrays

Ein Array ist eine Datenstruktur, die zum Sammeln mehrerer Datenelemente desselben Datentyps in einer Variablen verwendet wird. Anstatt mehrere Werte desselben Datentyps in separaten Variablennamen zu speichern, könnten wir sie alle zusammen in einer Variablen speichern. Diese Aussage bedeutet nicht, dass wir alle Werte desselben Datentyps in einem beliebigen Programm in einem Array dieses Datentyps vereinen müssen. Es kommt jedoch häufig vor, dass bestimmte Variablen desselben Datentyps in einer für ein Array geeigneten Weise miteinander in Beziehung stehen.

Ein Array ist eine Liste von Elementen, wobei jedes Element einen eindeutigen Platz in der Liste hat. Die Datenelemente des Arrays haben denselben Variablennamen; jedoch trägt jedes eine andere Indexnummer, die als Index bezeichnet wird. Wir können auf jedes Datenelement aus der Liste mithilfe seiner Position in der Liste zugreifen. Das wichtigste zu verstehende Merkmal der Arrays besteht also darin, dass die Daten an zusammenhängenden Speicherorten gespeichert werden, was es den Benutzern ermöglicht, die Datenelemente des Arrays mithilfe ihrer jeweiligen Indizes zu durchlaufen.

Figur 3. Eine Anordnung

Arrays können in verschiedene Typen eingeteilt werden:

Eindimensionales Array:Ein Array mit nur einer Zeile von Datenelementen wird als eindimensionales Array bezeichnet. Die Speicherung erfolgt in aufsteigender Reihenfolge.Zweidimensionales Array:Ein Array, das aus mehreren Zeilen und Spalten von Datenelementen besteht, wird als zweidimensionales Array bezeichnet. Es wird auch als Matrix bezeichnet.Mehrdimensionales Array:Wir können ein mehrdimensionales Array als ein Array von Arrays definieren. Mehrdimensionale Arrays sind nicht an zwei Indizes oder zwei Dimensionen gebunden, da sie je nach Bedarf beliebig viele Indizes enthalten können.

Einige Anwendungen von Array:

1. Wir können eine Liste von Datenelementen speichern, die zum gleichen Datentyp gehören.
2. Array fungiert als Hilfsspeicher für andere Datenstrukturen.
3. Das Array hilft auch beim Speichern von Datenelementen eines Binärbaums mit fester Anzahl.
4. Array fungiert auch als Speicher für Matrizen.

2. Verknüpfte Listen

A Verlinkte Liste ist ein weiteres Beispiel für eine lineare Datenstruktur, die zum dynamischen Speichern einer Sammlung von Datenelementen verwendet wird. Datenelemente in dieser Datenstruktur werden durch die Knoten dargestellt, die über Links oder Zeiger verbunden sind. Jeder Knoten enthält zwei Felder, das Informationsfeld besteht aus den tatsächlichen Daten und das Zeigerfeld besteht aus der Adresse der nachfolgenden Knoten in der Liste. Der Zeiger des letzten Knotens der verknüpften Liste besteht aus einem Nullzeiger, da er auf nichts zeigt. Im Gegensatz zu Arrays kann der Benutzer die Größe einer verknüpften Liste dynamisch an die Anforderungen anpassen.

Windows-Befehl arp

Figur 4. Eine verknüpfte Liste

Verknüpfte Listen können in verschiedene Typen eingeteilt werden:

Einfach verlinkte Liste:Eine einfach verknüpfte Liste ist der häufigste Typ einer verknüpften Liste. Jeder Knoten verfügt über Daten und ein Zeigerfeld, das eine Adresse zum nächsten Knoten enthält.Doppelt verknüpfte Liste:Eine doppelt verknüpfte Liste besteht aus einem Informationsfeld und zwei Zeigerfeldern. Das Informationsfeld enthält die Daten. Das erste Zeigerfeld enthält eine Adresse des vorherigen Knotens, während ein anderes Zeigerfeld eine Referenz auf den nächsten Knoten enthält. Somit können wir in beide Richtungen gehen (sowohl rückwärts als auch vorwärts).Zirkular verlinkte Liste:Die zirkulär verknüpfte Liste ähnelt der einfach verknüpften Liste. Der einzige wesentliche Unterschied besteht darin, dass der letzte Knoten die Adresse des ersten Knotens enthält und so eine kreisförmige Schleife in der Circular Linked List bildet.

Einige Anwendungen verknüpfter Listen:

1. Die verknüpften Listen helfen uns bei der Implementierung von Stapeln, Warteschlangen, Binärbäumen und Diagrammen vordefinierter Größe.
2. Wir können auch die Funktion des Betriebssystems für die dynamische Speicherverwaltung implementieren.
3. Verknüpfte Listen ermöglichen auch die Polynomimplementierung für mathematische Operationen.
4. Wir können Circular Linked List verwenden, um Betriebssysteme oder Anwendungsfunktionen zu implementieren, die die Round-Robin-Ausführung von Aufgaben ermöglichen.
5. Eine kreisförmige verknüpfte Liste ist auch in einer Diashow hilfreich, wenn ein Benutzer nach der Präsentation der letzten Folie zur ersten Folie zurückkehren muss.
6. Eine doppelt verknüpfte Liste wird verwendet, um Vorwärts- und Rückwärtsschaltflächen in einem Browser zu implementieren, um auf den geöffneten Seiten einer Website vorwärts und rückwärts zu navigieren.

3. Stapel

A Stapel ist eine lineare Datenstruktur, die dem folgt LIFO (Last In, First Out)-Prinzip, das Vorgänge wie das Einfügen und Löschen an einem Ende des Stapels, d. h. oben, ermöglicht. Stapel können mit Hilfe von zusammenhängendem Speicher, einem Array, und nicht zusammenhängendem Speicher, einer verknüpften Liste, implementiert werden. Beispiele für Stacks aus dem wirklichen Leben sind Bücherstapel, ein Kartenspiel, Geldhaufen und vieles mehr.

Abbildung 5. Ein reales Beispiel für Stack

Die obige Abbildung stellt das reale Beispiel eines Stapels dar, bei dem die Vorgänge nur von einem Ende aus ausgeführt werden, z. B. das Einlegen und Entfernen neuer Bücher von der Oberseite des Stapels. Dies impliziert, dass das Einfügen und Löschen in den Stapel nur von der Oberseite des Stapels aus erfolgen kann. Wir können zu jedem Zeitpunkt nur auf die Spitzen des Stapels zugreifen.

Die primären Operationen im Stack sind wie folgt:

Drücken:Der Vorgang zum Einfügen eines neuen Elements in den Stapel wird als Push-Vorgang bezeichnet.Pop:Der Vorgang zum Entfernen oder Löschen von Elementen aus dem Stapel wird als Pop-Vorgang bezeichnet.

Abbildung 6. Ein Stapel

Einige Anwendungen von Stacks:

1. Der Stack wird als temporäre Speicherstruktur für rekursive Operationen verwendet.
2. Der Stapel wird auch als Hilfsspeicherstruktur für Funktionsaufrufe, verschachtelte Operationen und verzögerte/aufgeschobene Funktionen verwendet.
3. Wir können Funktionsaufrufe mithilfe von Stacks verwalten.
4. Stapel werden auch verwendet, um arithmetische Ausdrücke in verschiedenen Programmiersprachen auszuwerten.
5. Stapel sind auch hilfreich bei der Konvertierung von Infix-Ausdrücken in Postfix-Ausdrücke.
6. Mithilfe von Stacks können wir die Syntax des Ausdrucks in der Programmierumgebung überprüfen.
7. Mit Stacks können wir Klammern zuordnen.
8. Stapel können verwendet werden, um einen String umzukehren.
9. Stacks sind hilfreich bei der Lösung von Problemen, die auf Backtracking basieren.
10. Wir können Stacks für die Tiefensuche bei der Graph- und Baumdurchquerung verwenden.
11. Stapel werden auch in Betriebssystemfunktionen verwendet.
12. Stapel werden auch in den UNDO- und REDO-Funktionen einer Bearbeitung verwendet.

4. Schwänze

A Warteschlange ist eine lineare Datenstruktur ähnlich einem Stapel mit einigen Einschränkungen beim Einfügen und Löschen der Elemente. Das Einfügen eines Elements in eine Warteschlange erfolgt an einem Ende und das Entfernen an einem anderen oder gegenüberliegenden Ende. Daraus können wir schließen, dass die Warteschlangendatenstruktur dem FIFO-Prinzip (First In, First Out) folgt, um die Datenelemente zu manipulieren. Die Implementierung von Warteschlangen kann mithilfe von Arrays, verknüpften Listen oder Stapeln erfolgen. Einige Beispiele aus dem wirklichen Leben für Warteschlangen sind eine Schlange am Ticketschalter, eine Rolltreppe, eine Autowaschanlage und vieles mehr.

Abbildung 7. Ein reales Beispiel für eine Warteschlange

Das obige Bild ist eine reale Abbildung eines Kinokartenschalters, die uns helfen kann, die Warteschlange zu verstehen, in der der Kunde, der zuerst kommt, immer zuerst bedient wird. Der zuletzt ankommende Kunde wird zweifellos als Letzter bedient. Beide Enden der Warteschlange sind offen und können verschiedene Operationen ausführen. Ein weiteres Beispiel ist eine Food-Court-Linie, bei der der Kunde am hinteren Ende eingeführt wird, während er am vorderen Ende entfernt wird, nachdem er den gewünschten Service erbracht hat.

Im Folgenden sind die Hauptoperationen der Warteschlange aufgeführt:

In die Warteschlange stellen:Das Einfügen oder Hinzufügen einiger Datenelemente zur Warteschlange wird als Enqueue bezeichnet. Das Einfügen von Elementen erfolgt immer mit Hilfe des hinteren Zeigers.Aus der Warteschlange entfernen:Das Löschen oder Entfernen von Datenelementen aus der Warteschlange wird als Dequeue bezeichnet. Das Löschen des Elements erfolgt immer mit Hilfe des Frontzeigers.

Abbildung 8. Warteschlange

Einige Anwendungen von Warteschlangen:

1. Warteschlangen werden im Allgemeinen bei der Breitensuchoperation in Diagrammen verwendet.
2. Warteschlangen werden auch in Job Scheduler-Vorgängen von Betriebssystemen verwendet, z. B. eine Tastaturpufferwarteschlange zum Speichern der von Benutzern gedrückten Tasten und eine Druckpufferwarteschlange zum Speichern der vom Drucker gedruckten Dokumente.
3. Warteschlangen sind für die CPU-Planung, Jobplanung und Festplattenplanung verantwortlich.
4. Prioritätswarteschlangen werden beim Herunterladen von Dateien in einem Browser verwendet.
5. Warteschlangen werden auch zum Übertragen von Daten zwischen Peripheriegeräten und der CPU verwendet.
6. Warteschlangen sind auch für die Verarbeitung von Interrupts verantwortlich, die von den Benutzeranwendungen für die CPU generiert werden.

Nichtlineare Datenstrukturen

Nichtlineare Datenstrukturen sind Datenstrukturen, bei denen die Datenelemente nicht in sequentieller Reihenfolge angeordnet sind. Hier ist das Einfügen und Entfernen von Daten nicht linear möglich. Zwischen den einzelnen Datenelementen besteht eine hierarchische Beziehung.

Arten nichtlinearer Datenstrukturen

Das Folgende ist die Liste der nichtlinearen Datenstrukturen, die wir im Allgemeinen verwenden:

Teilzeichenfolge Java

1. Bäume

Ein Baum ist eine nichtlineare Datenstruktur und eine Hierarchie, die eine Sammlung von Knoten enthält, sodass jeder Knoten des Baums einen Wert und eine Liste von Verweisen auf andere Knoten (die „Kinder“) speichert.

Die Baumdatenstruktur ist eine spezielle Methode zum Ordnen und Sammeln von Daten im Computer, um sie effektiver nutzen zu können. Es enthält einen zentralen Knoten, Strukturknoten und über Kanten verbundene Unterknoten. Wir können auch sagen, dass die Baumdatenstruktur aus verbundenen Wurzeln, Zweigen und Blättern besteht.

Abbildung 9. Ein Baum

Bäume können in verschiedene Arten eingeteilt werden:

Binärbaum:Eine Baumdatenstruktur, bei der jeder übergeordnete Knoten höchstens zwei untergeordnete Knoten haben kann, wird als Binärbaum bezeichnet.Binärer Suchbaum:Ein binärer Suchbaum ist eine Baumdatenstruktur, in der wir problemlos eine sortierte Liste von Zahlen verwalten können.AVL-Baum:Ein AVL-Baum ist ein selbstausgleichender binärer Suchbaum, bei dem jeder Knoten zusätzliche Informationen verwaltet, die als Balance-Faktor bekannt sind und dessen Wert entweder -1, 0 oder +1 ist.B-Baum:Ein B-Baum ist eine spezielle Art eines selbstausgleichenden binären Suchbaums, bei dem jeder Knoten aus mehreren Schlüsseln besteht und mehr als zwei untergeordnete Knoten haben kann.

Einige Anwendungen von Bäumen:

1. Bäume implementieren hierarchische Strukturen in Computersystemen wie Verzeichnissen und Dateisystemen.
2. Bäume werden auch verwendet, um die Navigationsstruktur einer Website zu implementieren.
3. Mit Trees können wir Code wie Huffmans Code generieren.
4. Bäume sind auch bei der Entscheidungsfindung in Gaming-Anwendungen hilfreich.
5. Bäume sind für die Implementierung von Prioritätswarteschlangen für prioritätsbasierte Betriebssystemplanungsfunktionen verantwortlich.
6. Bäume sind auch für das Parsen von Ausdrücken und Anweisungen in den Compilern verschiedener Programmiersprachen verantwortlich.
7. Wir können Bäume verwenden, um Datenschlüssel für die Indizierung für das Datenbankverwaltungssystem (DBMS) zu speichern.
8. Spanning Trees ermöglicht es uns, Entscheidungen in Computer- und Kommunikationsnetzwerken weiterzuleiten.
9. Bäume werden auch im Pfadfindungsalgorithmus verwendet, der in Anwendungen für künstliche Intelligenz (KI), Robotik und Videospiele implementiert ist.

2. Diagramme

Ein Graph ist ein weiteres Beispiel für eine nichtlineare Datenstruktur, die aus einer endlichen Anzahl von Knoten oder Eckpunkten und den sie verbindenden Kanten besteht. Die Diagramme werden verwendet, um Probleme der realen Welt anzugehen, indem sie den Problembereich als Netzwerk wie soziale Netzwerke, Leitungsnetzwerke und Telefonnetzwerke bezeichnen. Beispielsweise können die Knoten oder Eckpunkte eines Graphen einen einzelnen Benutzer in einem Telefonnetz darstellen, während die Kanten die Verbindung zwischen ihnen per Telefon darstellen.

Die Graph-Datenstruktur G wird als mathematische Struktur betrachtet, die aus einer Reihe von Eckpunkten V und einer Reihe von Kanten E besteht, wie unten gezeigt:

G = (V,E)

Abbildung 10. Ein Graph

Die obige Abbildung stellt einen Graphen mit sieben Eckpunkten A, B, C, D, E, F, G und zehn Kanten [A, B], [A, C], [B, C], [B, D] dar. [B, E], [C, D], [D, E], [D, F], [E, F] und [E, G].

Abhängig von der Position der Eckpunkte und Kanten können die Diagramme in verschiedene Typen eingeteilt werden:

Nulldiagramm:Ein Graph mit einer leeren Kantenmenge wird als Nullgraph bezeichnet.Triviales Diagramm:Ein Graph mit nur einem Knoten wird als Trivialgraph bezeichnet.Einfaches Diagramm:Ein Graph ohne Selbstschleifen oder mehrere Kanten wird als einfacher Graph bezeichnet.Multi-Graph:Ein Graph wird als Multi bezeichnet, wenn er aus mehreren Kanten, aber keinen Selbstschleifen besteht.Pseudograph:Ein Graph mit Selbstschleifen und mehreren Kanten wird als Pseudograph bezeichnet.Ungerichteter Graph:Ein Graph, der aus ungerichteten Kanten besteht, wird als ungerichteter Graph bezeichnet.Gerichteter Graph:Ein Graph, der aus den gerichteten Kanten zwischen den Eckpunkten besteht, wird als gerichteter Graph bezeichnet.Verbundenes Diagramm:Ein Graph mit mindestens einem einzigen Pfad zwischen jedem Eckpunktpaar wird als verbundener Graph bezeichnet.Nicht verbundenes Diagramm:Ein Diagramm, bei dem es keinen Pfad zwischen mindestens einem Scheitelpunktpaar gibt, wird als getrenntes Diagramm bezeichnet.Regelmäßiges Diagramm:Ein Graph, bei dem alle Eckpunkte den gleichen Grad haben, wird als regulärer Graph bezeichnet.Vollständige Grafik:Ein Graph, in dem alle Eckpunkte eine Kante zwischen jedem Eckpunktpaar haben, wird als vollständiger Graph bezeichnet.Zyklusdiagramm:Ein Graph wird als Zyklus bezeichnet, wenn er mindestens drei Eckpunkte und Kanten hat, die einen Zyklus bilden.Zyklischer Graph:Ein Graph wird genau dann als zyklisch bezeichnet, wenn mindestens ein Zyklus existiert.Azyklischer Graph:Ein Graph mit null Zyklen wird als azyklischer Graph bezeichnet.Endlicher Graph:Ein Graph mit einer endlichen Anzahl von Eckpunkten und Kanten wird als endlicher Graph bezeichnet.Unendlicher Graph:Ein Graph mit unendlich vielen Ecken und Kanten wird als unendlicher Graph bezeichnet.Zweiteiliger Graph:Ein Graph, bei dem die Eckpunkte in unabhängige Mengen A und B unterteilt werden können und alle Eckpunkte von Satz A nur mit einigen Kanten mit den in Satz B vorhandenen Eckpunkten verbunden werden sollten, wird als bipartiter Graph bezeichnet.Planarer Graph:Ein Graph wird als planar bezeichnet, wenn wir ihn in einer einzigen Ebene mit zwei einander schneidenden Kanten zeichnen können.Euler-Diagramm:Ein Graph wird genau dann als Euler-Graph bezeichnet, wenn alle Eckpunkte gerade Grade haben.Hamilton-Graph:Ein zusammenhängender Graph, der aus einem Hamilton-Kreis besteht, wird als Hamilton-Graph bezeichnet.

Einige Anwendungen von Diagrammen:

1. Mithilfe von Diagrammen können wir Routen und Netzwerke in Transport-, Reise- und Kommunikationsanwendungen darstellen.
2. Diagramme dienen zur Darstellung von Routen im GPS.
3. Diagramme helfen uns auch dabei, die Zusammenhänge in sozialen Netzwerken und anderen netzwerkbasierten Anwendungen darzustellen.
4. Diagramme werden in Kartenanwendungen verwendet.
5. Diagramme sind für die Darstellung der Benutzerpräferenzen in E-Commerce-Anwendungen verantwortlich.
6. Diagramme werden auch in Versorgungsnetzen verwendet, um die Probleme zu identifizieren, mit denen lokale oder kommunale Unternehmen konfrontiert sind.
7. Diagramme helfen auch dabei, die Nutzung und Verfügbarkeit von Ressourcen in einer Organisation zu verwalten.
8. Diagramme werden auch verwendet, um Dokument-Link-Maps der Websites zu erstellen, um die Konnektivität zwischen den Seiten über Hyperlinks anzuzeigen.
9. Graphen werden auch in Roboterbewegungen und neuronalen Netzen verwendet.

Grundlegende Operationen von Datenstrukturen

Im folgenden Abschnitt besprechen wir die verschiedenen Arten von Operationen, die wir durchführen können, um Daten in jeder Datenstruktur zu manipulieren:

Durchquerung:Das Durchlaufen einer Datenstruktur bedeutet, dass auf jedes Datenelement genau einmal zugegriffen wird, um es verwalten zu können. Beispielsweise ist beim Drucken der Namen aller Mitarbeiter einer Abteilung ein Durchlauf erforderlich.Suchen:Die Suche ist eine weitere Datenstrukturoperation, bei der es darum geht, den Speicherort eines oder mehrerer Datenelemente zu finden, die bestimmte Einschränkungen erfüllen. Ein solches Datenelement kann in der gegebenen Menge von Datenelementen vorhanden sein oder auch nicht. Mit der Suchfunktion können wir beispielsweise die Namen aller Mitarbeiter finden, die über eine Berufserfahrung von mehr als 5 Jahren verfügen.Einfügung:Einfügen bedeutet das Einfügen oder Hinzufügen neuer Datenelemente zur Sammlung. Mit dem Einfügevorgang können wir beispielsweise die Details eines neuen Mitarbeiters hinzufügen, den das Unternehmen kürzlich eingestellt hat.Streichung:Unter Löschen versteht man das Entfernen oder Löschen eines bestimmten Datenelements aus der angegebenen Liste von Datenelementen. Mit dem Löschvorgang können wir beispielsweise den Namen eines Mitarbeiters löschen, der den Job verlassen hat.Sortierung:Sortieren bedeutet, die Datenelemente je nach Art der Anwendung entweder in aufsteigender oder absteigender Reihenfolge anzuordnen. Mit der Sortieroperation können wir beispielsweise die Namen der Mitarbeiter einer Abteilung in alphabetischer Reihenfolge anordnen oder die drei besten Mitarbeiter des Monats schätzen, indem wir die Leistung der Mitarbeiter in absteigender Reihenfolge anordnen und die Details der drei besten Mitarbeiter extrahieren.Verschmelzen:Zusammenführen bedeutet, Datenelemente zweier sortierter Listen zu kombinieren, um eine einzige Liste sortierter Datenelemente zu bilden.Erstellen:Erstellen ist eine Operation, mit der Speicher für die Datenelemente des Programms reserviert wird. Wir können diesen Vorgang mithilfe einer Deklarationsanweisung ausführen. Die Erstellung der Datenstruktur kann wie folgt erfolgen:
1. Kompilierzeit
2. Laufzeit
   Zum Beispiel die malloc() Die Funktion wird in der C-Sprache zum Erstellen einer Datenstruktur verwendet.
Auswahl:Unter Auswahl versteht man die Auswahl bestimmter Daten aus den verfügbaren Daten. Wir können bestimmte Daten auswählen, indem wir Bedingungen innerhalb der Schleife angeben.Aktualisieren:Mit der Update-Operation können wir die Daten in der Datenstruktur aktualisieren oder ändern. Wir können auch bestimmte Daten aktualisieren, indem wir einige Bedingungen innerhalb der Schleife angeben, wie zum Beispiel die Auswahloperation.Aufteilung:Der Splitting-Vorgang ermöglicht es uns, Daten in verschiedene Unterteile aufzuteilen und so die Gesamtzeit für den Abschluss des Prozesses zu verkürzen.

Den abstrakten Datentyp verstehen

Gemäß der Nationales Institut für Standards und Technologie (NIST) Eine Datenstruktur ist eine Anordnung von Informationen, im Allgemeinen im Speicher, zur Verbesserung der Algorithmuseffizienz. Zu den Datenstrukturen gehören verknüpfte Listen, Stapel, Warteschlangen, Bäume und Wörterbücher. Sie könnten auch eine theoretische Einheit sein, etwa der Name und die Adresse einer Person.

Aus der oben genannten Definition können wir schließen, dass die Operationen in der Datenstruktur Folgendes umfassen:

1. Ein hohes Abstraktionsniveau wie das Hinzufügen oder Löschen eines Elements aus einer Liste.
2. Suchen und Sortieren eines Elements in einer Liste.
3. Zugriff auf das Element mit der höchsten Priorität in einer Liste.

Immer wenn die Datenstruktur solche Operationen ausführt, wird sie als bezeichnet Abstrakter Datentyp (ADT) .

Wir können es als eine Reihe von Datenelementen zusammen mit den Operationen an den Daten definieren. Der Begriff „abstrakt“ bezieht sich auf die Tatsache, dass die Daten und die darauf definierten grundlegenden Operationen unabhängig von ihrer Implementierung untersucht werden. Es geht darum, was wir mit den Daten machen können, nicht wie wir es machen können.

Pfad in Java festgelegt

Eine ADI-Implementierung enthält eine Speicherstruktur, um die Datenelemente und Algorithmen für den grundlegenden Betrieb zu speichern. Alle Datenstrukturen, wie ein Array, eine verknüpfte Liste, eine Warteschlange, ein Stapel usw., sind Beispiele für ADT.

Die Vorteile der Verwendung von ADTs verstehen

In der realen Welt entwickeln sich Programme aufgrund neuer Einschränkungen oder Anforderungen weiter. Daher erfordert die Änderung eines Programms im Allgemeinen eine Änderung einer oder mehrerer Datenstrukturen. Angenommen, wir möchten ein neues Feld in den Datensatz eines Mitarbeiters einfügen, um weitere Details zu jedem Mitarbeiter zu verfolgen. In diesem Fall können wir die Effizienz des Programms verbessern, indem wir ein Array durch eine Linked-Struktur ersetzen. In einer solchen Situation ist es ungeeignet, jede Prozedur neu zu schreiben, die die geänderte Struktur verwendet. Daher besteht eine bessere Alternative darin, eine Datenstruktur von ihren Implementierungsinformationen zu trennen. Dies ist das Prinzip hinter der Verwendung von Abstract Data Types (ADT).

Einige Anwendungen von Datenstrukturen

Im Folgenden sind einige Anwendungen von Datenstrukturen aufgeführt:

1. Datenstrukturen helfen bei der Organisation von Daten im Speicher eines Computers.
2. Datenstrukturen helfen auch bei der Darstellung der Informationen in Datenbanken.
3. Datenstrukturen ermöglichen die Implementierung von Algorithmen zum Durchsuchen von Daten (z. B. einer Suchmaschine).
4. Wir können die Datenstrukturen verwenden, um die Algorithmen zur Datenbearbeitung zu implementieren (z. B. Textverarbeitungsprogramme).
5. Wir können die Algorithmen auch implementieren, um Daten mithilfe von Datenstrukturen zu analysieren (z. B. Data Miner).
6. Datenstrukturen unterstützen Algorithmen zum Generieren der Daten (z. B. einen Zufallszahlengenerator).
7. Datenstrukturen unterstützen auch Algorithmen zum Komprimieren und Dekomprimieren der Daten (z. B. ein Zip-Dienstprogramm).
8. Wir können Datenstrukturen auch verwenden, um Algorithmen zum Ver- und Entschlüsseln der Daten zu implementieren (z. B. ein Sicherheitssystem).
9. Mithilfe von Datenstrukturen können wir Software erstellen, die Dateien und Verzeichnisse verwalten kann (z. B. einen Dateimanager).
10. Wir können auch Software entwickeln, die Grafiken mithilfe von Datenstrukturen rendern kann. (Zum Beispiel ein Webbrowser oder eine 3D-Rendering-Software).

Abgesehen davon gibt es, wie bereits erwähnt, viele andere Anwendungen von Datenstrukturen, die uns bei der Erstellung jeder gewünschten Software helfen können.