Zinseszinsen sind die Zinsen, die auf einen Kredit- oder Einlagenbetrag berechnet werden, wobei Zinsen für den Kapitalbetrag sowie die zuvor verdienten Zinsen berechnet werden.

Der gemeinsame Unterschied zwischen Zinseszins und einfachem Zins liegt darin Zinseszins Die Zinsen werden sowohl für den Kapitalbetrag als auch für die zuvor erwirtschafteten Zinsen berechnet, während der einfache Zins nur vom investierten Kapital abhängt.

Inhaltsverzeichnis

• Was ist Zinseszins?
• Zinseszinsformel
• Wie berechnet man den Zinseszins?
• Zinseszinsformel – Ableitung
• Halbjährliche Zinseszinsformel
• Vierteljährliche Zinseszinsformel
• Monatliche Zinseszinsformel
• Tägliche Zinseszinsformel
• Formel für die periodische Aufzinsungsrate
• Regel von 72
• Zinseszins aufeinanderfolgender Jahre
• Kontinuierliche Zinseszinsformel
• Einige andere Anwendungen des Zinseszinses
• Unterschied zwischen Zinseszins und einfachem Zins
• Beispiele für Zinseszinsen
• Zinseszins – Übungsfragen

Was ist Zinseszins?

Zinseszinsen sind Zinsen auf den Kapitalbetrag sowie die auf den Kapitalbetrag erwirtschafteten Zinsen. Das Wort Zinseszins besteht aus zwei Wörtern Zusammengesetzt bedeutet, dass es sich aus zwei oder mehr zusammensetzt, und Zinsen bedeuten Geld, das durch die Ausleihe des Betrags verdient wird. Daher ist der Zinseszins das mit der Kreditvergabe verdiente Geld und setzt sich aus zwei Arten von Zinsen zusammen:

• Zinsen auf den Kapitalbetrag

• Zinsen auf Zinsen, die im Laufe des Zeitraums auf den Kapitalbetrag erwirtschaftet wurden

Zinseszins-Definition

Zinseszins ist der Zins, der auf den Kapitalbetrag und die zuvor verdienten Zinsen berechnet wird. Es wird mit C.I. bezeichnet. Es ist sehr nützlich für Investitions- und Kreditrückzahlungszwecke. Es wird auch als Zins auf Zins bezeichnet.

Latexliste

Zinseszins ist im Banken- und Finanzsektor sehr nützlich und ist auch in anderen Sektoren nützlich. Einige seiner Verwendungsmöglichkeiten sind:

• Wachstum der Bevölkerung eines Landes
• Wert der Investition über einen bestimmten Zeitraum.
• Zur Ermittlung überhöhter Kosten und des Wertverlusts eines Artikels.
• Zur Vorhersage des Wachstums einer Institution oder eines Landes.

Zinseszins (C.I) = Betrag – Kapital

Zinseszinsformel

Zinseszins wird berechnet, nachdem der Gesamtbetrag über einen bestimmten Zeitraum auf der Grundlage des Zinssatzes und des ursprünglichen Kapitalbetrags berechnet wurde. Für einen anfänglichen Kapitalbetrag von P, einen jährlichen Zinssatz von r, einen Zeitraum t in Jahren und die Häufigkeit der jährlichen Aufzinsung der Zinsen n lautet die Formel zur Berechnung von CI wie folgt:

CI = P(1 + r/100) ^N - P

Die obige Formel zur Berechnung des Zinseszinses wird in der folgenden Bildform hinzugefügt:

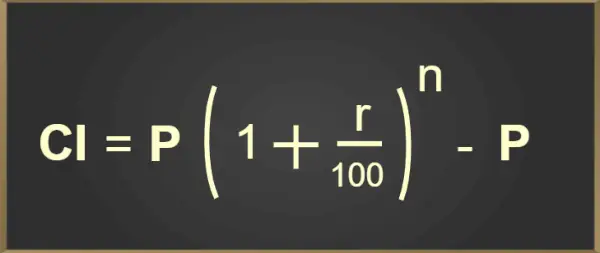
Zinseszinsformel

Wo,

• P = Haupt
• r = Zinssatz
• n = Anzahl der Zinseszinsen pro Jahr
• t = Zeit (in Jahren)

Wir können die Formel für den Zinseszins wie folgt schreiben:

Zinseszins = A – P

Wo,

• A = Gesamtbetrag nach der Aufzinsung
• P = Anfänglicher Kapitalbetrag

Zinseszins = P(1 + r/n) ^nt -P

Wo,

• P = Anfänglicher Kapitalbetrag
• r = Jährlicher Zinssatz
• n = Anzahl der Zinseszinsen
• t = Anzahl der Jahre

Der Zinseszins kann je nach Anforderung jährlich, halbjährlich, vierteljährlich, monatlich, täglich usw. berechnet werden.

Wie berechnet man den Zinseszins?

Zinseszins ist der Zins, der sowohl auf das Kapital als auch auf die aufgelaufenen Zinsen gezahlt wird. Die in jedem Intervall verdienten Zinsen werden zum anfänglichen Kapital addiert, sodass sich das Kapital weiter erhöht.

Verwenden Sie die folgenden Methoden, um den Zinseszins zu ermitteln.

Schritt 1: Hinweis, Kapital, Rate und Zeitraum angegeben

Schritt 2: Berechnen Sie den Betrag mit der Formel A = P(1 + r/100) ^N

Schritt 3: Finden Sie den Zinseszins mithilfe der Formel CI = Betrag – Kapital

In regelmäßigen Abständen werden die bisher aufgelaufenen Zinsen mit dem bestehenden Kapitalbetrag verrechnet und anschließend die Zinsen berechnet für den neuen Auftraggeber berechnet . Der neue Kapitalbetrag entspricht der Summe aus dem ursprünglichen Kapital und den bisher aufgelaufenen Zinsen.

Zinseszins = Zinsen auf Kapital + Zinsen auf Zinsen auf Kapital (ab dem zweiten Jahr und für sich selbst)

Der Zinseszins wird in regelmäßigen Abständen berechnet, z. B. jährlich (jährlich), halbjährlich, vierteljährlich, monatlich. usw; Es ist so, als würde die Reinvestition der Zinserträge aus einer Investition dazu führen, dass das Geld mit der Zeit schneller wächst! Es ist genau das, was der Zinseszins mit dem Geld macht. Banken oder andere Finanzinstitute berechnen den Betrag ausschließlich auf der Grundlage des Zinseszinses.

Zinseszinsformel – Ableitung

Die Zinseszinsformel ist ein leistungsstarkes Instrument, das im Finanzwesen zur Berechnung der auf einen anfänglichen Kapitalbetrag verdienten oder gezahlten Zinsen verwendet wird. Dies umfasst sowohl den ursprünglichen Kapitalbetrag als auch die in früheren Zeiträumen aufgelaufenen Zinsen. Die Formel für den Zinseszins ergibt sich aus:

Wo,

• A ist der zukünftige Wert der Investition oder des Darlehens, einschließlich Zinsen
• P ist der Kapitalbetrag (Anfangsinvestition oder Kreditbetrag)
• r ist der jährliche Zinssatz (als Dezimalzahl)
• n ist die Häufigkeit, mit der die Zinsen pro Jahr aufgezinst werden
• t ist die Zeit in Jahren, für die Geld investiert oder geliehen wird

Einfache Zinsformel

Einfache Zinsen werden nur auf den Kapitalbetrag berechnet. Es kann durch die Formel dargestellt werden ,

Zinseszinsformel mit kontinuierlicher Aufzinsung

Wenn die Zinsen kontinuierlich (unendlich oft pro Jahr) aufgezinst werden, wird die Formel für den Zinseszins aus der Formel für die kontinuierliche Aufzinsung abgeleitet:

Wo,

• e ist die Eulersche Zahl (ungefähr 2,71828)
• P ist der Kapitalbetrag
• r ist der jährliche Zinssatz
• t ist die Zeit in Jahren

Allgemeine Zinseszinsformel

Um die allgemeine Zinseszinsformel abzuleiten, betrachten wir den Zinseszins n-mal pro Jahr.

Wenn P wird n-mal pro Jahr zu einem jährlichen Zinssatz r verzinst, der Zins r wird durch n geteilt und n-mal pro Jahr angewendet. Nach t Jahren lautet die Formel also:

Wo,

• stellt den Zinssatz pro Zinsperiode dar.
• nt ist die Gesamtzahl der Zinsperioden über t Jahre.

Das Die Formel veranschaulicht, wie der anfängliche Kapitalbetrag im Laufe der Zeit wächst, wenn die Zinsen in regelmäßigen Abständen aufgezinst werden . Wenn sich n der Unendlichkeit nähert (d. h. kontinuierliche Compoundierung), konvergiert die Formel in Richtung der kontinuierlichen Compoundierungsformel .

In Summe, die Zinseszinsformel ist ein Ergebnis der kontinuierlichen Aufzinsungsformel, die für diskrete Aufzinsungsperioden pro Jahr angepasst wurde. Es ermöglicht die Berechnung des zukünftigen Wertes einer Investition oder eines Darlehens unter Berücksichtigung des Zinseszinses in regelmäßigen Abständen.

Halbjährliche Zinseszinsformel

Das investierte Kapital sei P und der Zinssatz sei R % pro Jahr, der halbjährlich für „t“ Jahre aufgezinst wird

Als es wird halbjährlich aufgezinst, der Kapitalbetrag wird nach Ablauf von 6 Monaten geändert, und die bis dahin verdienten Zinsen werden dem Kapital hinzugefügt und dieses wird dann zum neuen Kapital. Ebenso wird der Endbetrag berechnet.

Wir wissen,

Zinssatz = R% pro Jahr, halbjährlich verzinst

Rate = (R/2) %

Zeit ist t Jahre, wir wissen, dass t Jahre vergangen sind 2t Halbes Jahr.

Jetzt,

A = P (1 + R/200) ^2t

CI = A – P

Vierteljährliche Zinseszinsformel

Das investierte Kapital sei P und der Zinssatz sei R % pro Jahr, der vierteljährlich über t Jahre aufgezinst wird.

Als es wird vierteljährlich aufgezinst, der Kapitalbetrag wird am Ende von 3 Monaten geändert, Und Bis dahin verdiente Zinsen werden zum Kapital hinzugerechnet und bilden dann das neue Kapital. Ebenso wird der Endbetrag berechnet.

wir wissen,

Rate = R% pro Jahr, vierteljährlich aufgezinst

iskcon vollständiges Formular

Rate = (R/4)%

Zeit ist t Jahre, wir wissen, dass t Jahre vergangen sind 4t Viertel.

Jetzt,

A = P(1 + R/400) ^4t

CI = A – P

Überprüfen: Vierteljährliche Zinseszinsformel

Monatliche Zinseszinsformel

Wenn die Zinsen monatlich aufgezinst werden, beträgt die Anzahl der Aufzinsungen 12 und die Zinsen betragen jeden Monat 1/12 des jährlichen Zinseszinses. Daher wird die monatliche Zinseszinsformel wie folgt angegeben:

A = P[1 + (R/1200)] ^12t

CI = A – P

Überprüfen: Monatliche Zinseszinsformel

Tägliche Zinseszinsformel

Wenn die Zinsen täglich aufgezinst werden, dann.

Der neue Zinssatz beträgt R/365 %

n = 365

Daher lautet die tägliche Zinseszinsformel wie folgt:

A = P[1 + (R/36500)] ^365t

CI = A – P

Formel für die periodische Aufzinsungsrate

Der Gesamtbetrag, einschließlich Kapital P und Zinseszins CI, ergibt sich aus:

A = P[1 + (r/n)] ^nt

Wo,

• P = Haupt
• A = Endbetrag
• r = Jährlicher Zinssatz
• n = Anzahl der Zinseszinsen
• t = Zeit (in Jahren)

Somit ist der Zinseszins:

CI = A – P

Regel von 72

Die 72er-Regel ist die Formel, mit der geschätzt wird, wie viele Jahre sich unser Geld verdoppelt, wenn es jährlich aufgezinst wird. Für Beispiel , wenn unser Geld investiert ist R % Bei jährlicher Verzinsung dauert es 72/r Jahre, bis sich unser Geld verdoppelt.

Diese Berechnung ist auch nützlich, um den überhöhten Wert unseres Geldes zu berechnen. Das heißt, es gibt an, in wie vielen Jahren sich der Wert unseres Vermögenswerts halbiert, wenn er jährlich abgeschrieben wird.

Formel der Regel 72

Die folgende Formel wird verwendet, um ungefähr die Anzahl der Jahre zu ermitteln, in denen sich unsere Investition verdoppelt.

N = 72 / r

r in C-Sprache

Wo,

• N ist die ungefähre Anzahl der Jahre, in denen sich unser Geld verdoppelt
• R ist der Zinssatz, mit dem unser Geld jährlich verzinst wird

Beispiel für Regel 72

Angenommen, Kabir hat 10.000.000 Rupien in einen Schuldenfonds investiert, der eine Rendite von 8 % bringt. Finden Sie heraus, in wie vielen Jahren sich sein Geld verdoppelt, wenn es jährlich aufgezinst wird.

Unter Verwendung der obigen Formel: N = 72/8 = 9 Jahre

Daher, Es dauert 9 Jahre, bis sich Kabirs Geld verdoppelt.

Zinseszins aufeinanderfolgender Jahre

Wenn wir die gleiche Summe und den gleichen Zinssatz haben. Das C.I. eines bestimmten Jahres ist immer höher als der C.I. des Vorjahres. (CI des 3. Jahres ist größer als CI des 2. Jahres). Die Differenz zwischen CI für zwei aufeinanderfolgende Jahre ist der Zinssatz eines Jahres auf CI des Vorjahres.

C.I des 3. Jahres – C.I des 2. Jahres = C.I des 2. Jahres × r × 1/100

Die Differenz zwischen den Beträgen zweier aufeinanderfolgender Jahre ist der Zins eines Jahres auf den Betrag des Vorjahres.

Betrag des 3. Jahres – Betrag des 2. Jahres = Betrag des 2. Jahres × r × 1/100

Wichtigste Ergebnisse

Wenn wir die gleiche Summe und den gleichen Tarif haben ,

C.I für das n-te Jahr = C.I für das (n – 1)-te Jahr + Zinsen für ein Jahr auf C.I für das (n – 1)-te Jahr

Kontinuierliche Zinseszinsformel

Die kontinuierliche Aufzinsungsformel wird im Finanzwesen verwendet, um den Endwert einer Investition zu berechnen, die über verschiedene Zeiträume einer kontinuierlichen Aufzinsung unterliegt und im Laufe der Zeit einen Mehrwert schafft. Die Formel für die kontinuierliche Compoundierung lautet:

Endwert = Barwert × e ^rt

Wo,

• r ist der Zinssatz
• Es ist Zeit

Erfahren Sie mehr, Kontinuierliche Compoundierungsformel

Einige andere Anwendungen des Zinseszinses

Wachstum: Dies wird hauptsächlich für das Wachstum verwendet, wenn Branchen miteinander verbunden sind.

Produktion nach n Jahren = Anfangsproduktion × (1 + r/100) ^N

Wertminderung: Wenn die Kosten eines Produkts jedes Jahr um r % sinken, beträgt sein Wert nach n Jahren

Barwert × (1 + r/100) ^N

Bevölkerungsprobleme: Wenn die Bevölkerung einer Stadt oder eines Dorfes mit einer bestimmten Rate pro Jahr zunimmt.

Bevölkerung nach n Jahren = aktuelle Bevölkerung × (1 + r/100) ^N

Unterschied zwischen Zinseszins und einfachem Zins

Den Unterschied zwischen Zinseszins und einfachem Zins erfahren Sie weiter unten in diesem Artikel

Beispiele für Zinseszinsen

Einige Beispiele für Zinseszinsformeln sind:

Beispiel 1: Ermitteln Sie den Zinseszins, wenn der Kapitalbetrag = 6000 Rupien, der Zinssatz = 10 % pro Jahr und die Zeit = 2 Jahre beträgt.

Lösung:

Zinsen für das erste Jahr = (6000 × 10 × 1)/100 = 600

Betrag am Ende des ersten Jahres = 6000 + 600 = 6600

Zinsen für das zweite Jahr = (6600 × 10 × 1) / 100 = 660

Betrag am Ende des zweiten Jahres = 6600 + 660 = 7260

Zinseszins = 7260 – 6000 = 1260

Beispiel 2: Wie hoch wird der Zinseszins für 8.000 Rupien in zwei Jahren sein, wenn der Zinssatz 2 % pro Jahr beträgt?

Lösung:

Gegeben,

• Haupt-P = 8000
• Rate r = 2 %
• Zeit = 2 Jahre

nach Formel

A = P (1 + R/100) ^N

A = 8000 (1 + 2/100)²= 8000 (102/100)²

A = 8323

Zinseszins = A – P = 8323 – 8000 = Rs 323

Beispiel 3: Hari hat Rs eingezahlt. 4000 bei einer Finanzgesellschaft für 2 Jahre mit einem Zinssatz von 5 % pro Jahr. Wie hoch ist der Zinseszins, den Rohit nach 2 Jahren erhält?

Lösung:

Gegeben,

• Haupt-P = 4000
• Rate r = 5 %
• Zeit = 2 Jahre

Nach Formel,

A = P (1 + R/100)^N

A= 4000 (1 + 5/100)²

A= 4000 (105/100)²

A= 4410

Zinseszins = A – P = 4410 – 4000 = 410

Was ist Verzeichnisübermittlung?

Beispiel 4: Finden Sie den Zinseszins für Rs. 2000 mit einem Satz von 4 % pro Jahr für 1,5 Jahre. Wann werden die Zinsen halbjährlich berechnet?

Lösung:

Gegeben,

• Haupt p = 2000
• Rate r = 4 %
• Zeit = 1,5 (also 3 halbe Jahre)

nach Formel,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Zinseszins = A – P = 2122 – 2000 = 122

Beispiel 5: Wie hoch ist der Zinseszins auf 10000 für ein Jahr bei einem Zinssatz von 20 % pro Jahr, wenn der Zins vierteljährlich berechnet wird?

Lösung:

Gegeben,

• Kapital P = Rs 10000
• Rate R = 12 % (12/4 = 3 % pro Quartal)
• Zeit = 1 Jahr (1 × 4 = 4 Quartale)

Nach Formel,

A = P (1 + R/100) ^N

A = 10000 (1 + 3/100) ⁴

A = 10000 (103/100) ⁴

A = 11255

Zinseszins = A – P = 11255 – 10000 = 1255

Beispiel 6: Ermitteln Sie den Zinseszins in Höhe von 5 % pro Jahr für 2 Jahre auf den Kapitalbetrag, der in 2 Jahren in Höhe von 5 % pro Jahr gegeben ist. 400 als einfache Zinsen.

Lösung:

Gegeben,

• Einfaches Interesse IF = 400
• Rate R = 5 %
• Zeit T = 2 Jahre

Nach Formel,

Einfaches Interesse = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 Zinseszinssatz = 5 %

P = 40000/10 = Rs 4000

Zeit = 2 Jahre

Nach Formel,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Hallo Welt mit Java

Zinseszins = A – P = 4410 – 4000 = 410

Beispiel 7: Ermitteln Sie den Zinseszins für 30.000 Rupien bei 7 % Zinseszins pro Jahr für zwei Jahre.

Lösung:

• Kapital P = Rs 30000
• Rate R = 7 %
• Zeit = 2 Jahre

Nach Formel,

A = P (1 + R/100) ^N

A = 30000 (1 + 7/100) ²

A = 30000 (107/100) ²

A = 34347

Zinseszins = A – P = 34347 – 30000 = 4347

Verwandte Lektüre:

• Täglicher Zinseszins
• Monatlicher Zinseszins
• Zinseszinslösung der Klasse 8
• Zinseszins – Fragen und Antworten zur Eignung
• Einfaches Interesse

Zinseszins – Übungsfragen

Verschiedene Übungsfragen zum Thema Zinseszins sind:

Q1. Ermitteln Sie den Betrag, der nach 3 Jahren gezahlt werden muss, wenn ein Betrag von 10.000 zu einem jährlichen Zinssatz von 4 % geliehen wird.

Q2. Ermitteln Sie den Zinsbedarf, der nach 1,5 Jahren gezahlt werden muss, wenn ein Betrag von 2500 mit einem halbjährlichen Zinssatz von 6 % geliehen wird.

Q3. Berechnen Sie den Zinseszins für einen geliehenen Betrag von 9000 mit einem Zinssatz von 5 % vierteljährlich für 15 Monate.

Q4. Berechnen Sie den Zinseszins für einen geliehenen Betrag von 20000 mit einem Zinssatz von 12 % für 3 Monate, monatlich verzinst

Fazit zum Zinseszins

Zinseszins ist ein leistungsstarkes Finanzkonzept, das es ermöglicht, dass Investitionen oder Kredite im Laufe der Zeit wachsen oder sich ansammeln. nicht wie einfacher Zins, der nur Zinsen auf den ursprünglichen Kapitalbetrag berechnet, Zinseszins berücksichtigt die Zinsen, die sowohl auf den ursprünglichen Kapitalbetrag als auch auf alle aufgelaufenen Zinsen aus früheren Perioden entfallen.

Zinseszins – FAQs

Welche Bedeutung hat der Zinseszins?

Der Zinseszins ist der Zins, der auf den Kapitalbetrag sowie die zuvor über einen festgelegten Zeitraum erwirtschafteten Zinsen berechnet wird

Wie berechnet man den Zinseszins?

Um den Zinseszins zu berechnen, wird zunächst der Endbetrag berechnet und dann vom Kapital abgezogen, um den endgültigen Zinseszins zu erhalten. Der Betrag wird nach folgender Formel berechnet:

A = P(1 + R/100) ^T

CI = A – P

Ist der Zinseszins für Anleger besser als der einfache Zins?

Ja, der Zinseszins ist für Anleger weitaus besser als der einfache Zins.

Was ist die Zinseszinsformel, wenn sie täglich aufgezinst wird?

Angenommen, der gegebene Kapitalbetrag sei P, der Zinssatz sei R und das Zeitintervall sei T Jahre, dann lautet die Zinseszinsformel bei täglicher Aufzinsung:

A = P(1 + R/365) ^{{365 × T}}

Was ist der Unterschied zwischen CI und SI?

Der grundlegende Unterschied zwischen CI und SI besteht darin, dass es sich bei SI um Zinsen handelt, die auf den Kapitalbetrag erhoben werden, während es sich bei CI um Zinsen handelt, die auf den Kapitalbetrag sowie auf die auf dem Kapital aufgelaufenen Zinsen erhoben werden