In diesem Artikel werden wir die Inorder-Traversierung in der Datenstruktur diskutieren.
Wenn wir die Knoten in aufsteigender Reihenfolge durchlaufen möchten, verwenden wir die Inorder-Traversierung. Im Folgenden sind die Schritte aufgeführt, die für die Inorder-Traversierung erforderlich sind:
- Besuchen Sie alle Knoten im linken Teilbaum
- Besuchen Sie den Wurzelknoten
- Besuchen Sie alle Knoten im rechten Teilbaum
Lineare Datenstrukturen wie Stapel, Array, Warteschlange usw. haben nur eine Möglichkeit, die Daten zu durchlaufen. Aber in hierarchischen Datenstrukturen wie z Baum, Es gibt mehrere Möglichkeiten, die Daten zu durchlaufen. Hier diskutieren wir eine andere Möglichkeit, die Baumdatenstruktur zu durchqueren, nämlich die Inorder-Durchquerung.
Für die Inorder-Traversierung werden zwei Ansätze verwendet:
- Inorder-Traversal mit Rekursion
- Inorder-Durchlauf mit einer iterativen Methode
Es folgt eine Inorder-Traversal-Technik Linke Wurzel rechts Politik. Hier bedeutet Left Root Right, dass zuerst der linke Teilbaum des Wurzelknotens durchlaufen wird, dann der Wurzelknoten und dann der rechte Teilbaum des Wurzelknotens. Hier deutet der Inorder-Name selbst darauf hin, dass der Wurzelknoten zwischen dem linken und dem rechten Teilbaum liegt.
ist Eiweißfett
Wir werden die Inorder-Traversierung mit rekursiven und iterativen Techniken diskutieren. Beginnen wir zunächst mit der Inorder-Traversierung mittels Rekursion.
Inorder-Traversal mittels Rekursion
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Beispiel für Inorder-Traversal
Sehen wir uns nun ein Beispiel für eine Inorder-Traversierung an. Anhand eines Beispiels lässt sich die Vorgehensweise beim Inorder-Traversal leichter verstehen.
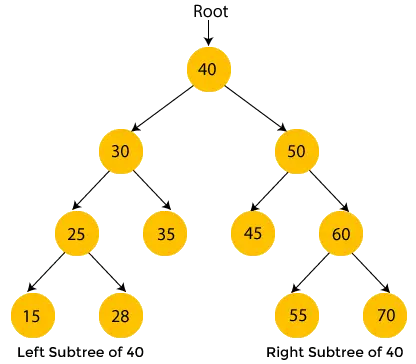
Die Knoten mit gelber Farbe wurden noch nicht besucht. Jetzt werden wir die Knoten des obigen Baums mithilfe der Inorder-Traversierung durchlaufen.
- Hier ist 40 der Wurzelknoten. Wir gehen zum linken Teilbaum von 40, also 30, und er hat auch den Teilbaum 25, also gehen wir wieder zum linken Teilbaum von 25, also 15. Hier hat 15 also keinen Teilbaum Drucken 15 und bewegen Sie sich in Richtung seines übergeordneten Knotens 25.
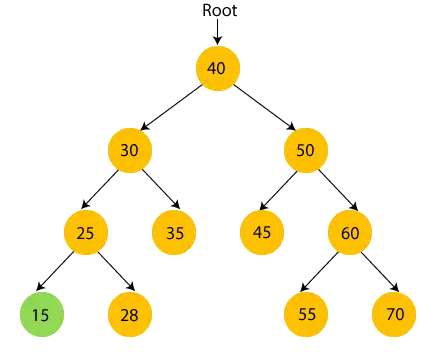
- Jetzt, Drucken 25 und gehe zum rechten Teilbaum von 25.
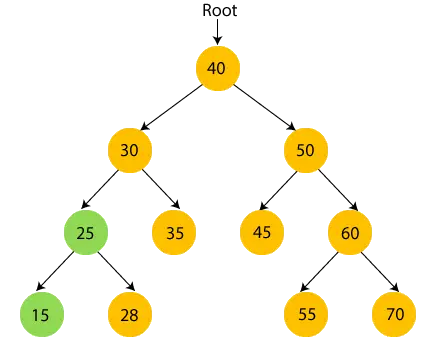
- Jetzt, Drucken 28 und gehe zum Wurzelknoten von 25, also 30.
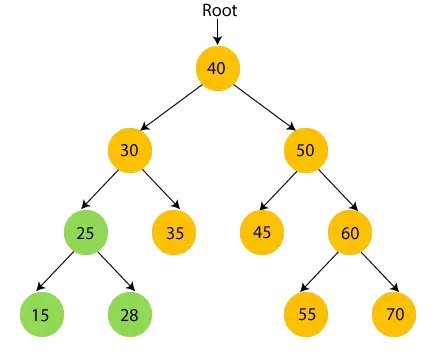
- Es wird also der linke Teilbaum von 30 besucht. Jetzt, Drucken 30 und zum rechten Kind von 30 wechseln.
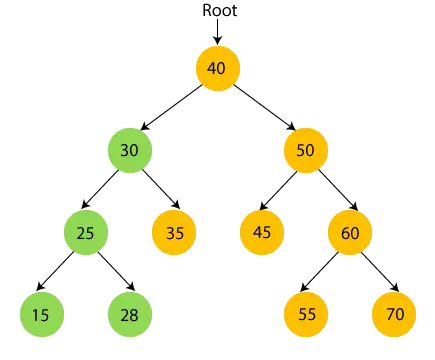
- Jetzt, Drucken 35 und gehe zum Wurzelknoten von 30.
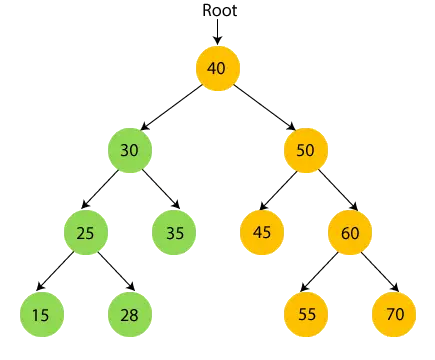
- Jetzt, Wurzelknoten 40 drucken und wechseln Sie zu seinem rechten Unterbaum.
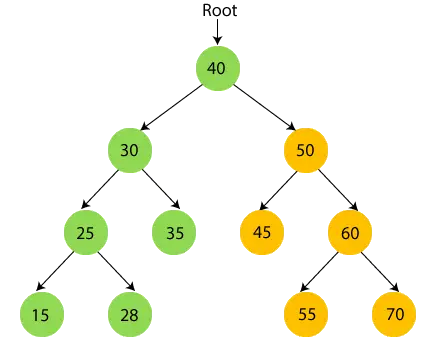
- Durchlaufen Sie nun rekursiv den rechten Teilbaum von 40, also 50.
50 haben einen Teilbaum, also durchqueren Sie zuerst den linken Teilbaum von 50, also 45. 45 hat also keine Kinder Drucken 45 und bewegen Sie sich zu seinem Wurzelknoten.
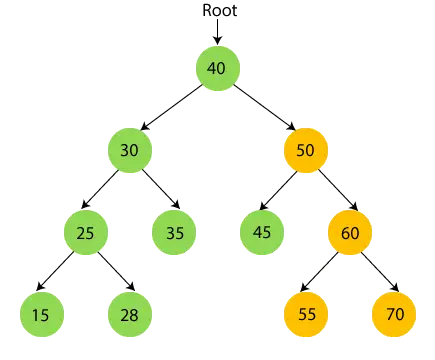
- Jetzt 50 drucken und gehe zum rechten Teilbaum von 50, also 60.
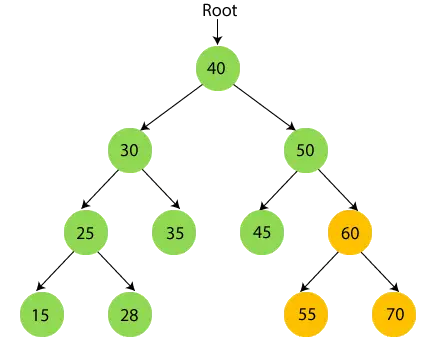
- Durchlaufen Sie nun rekursiv den rechten Teilbaum von 50, der 60 ist. 60 hat einen Teilbaum, also durchlaufen Sie zuerst den linken Teilbaum von 60, der 55 ist. 55 hat also keine Kinder Drucken 55 und bewegen Sie sich zu seinem Wurzelknoten.
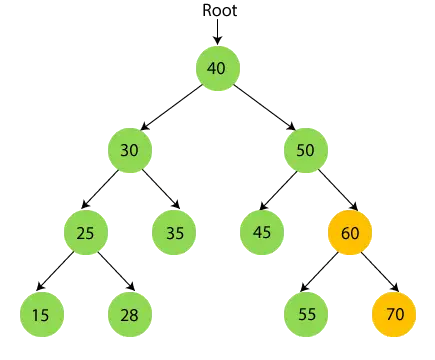
- Jetzt Drucken 60 und gehe zum rechten Teilbaum von 60, also 70.
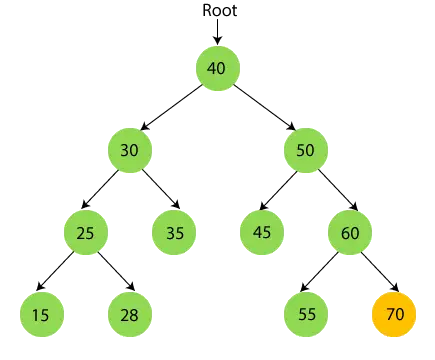
- Jetzt Drucken 70.
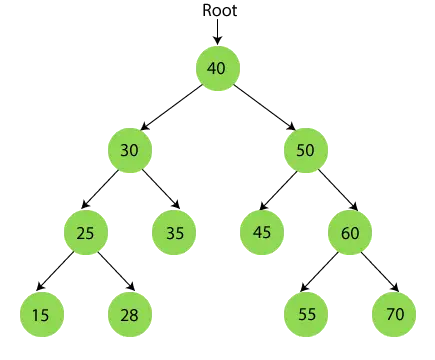
Nach Abschluss der Inorder-Durchquerung lautet die endgültige Ausgabe:
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Komplexität der Inorder-Durchquerung
Die zeitliche Komplexität der Inorder-Durchquerung beträgt An), Dabei ist „n“ die Größe des Binärbaums.
Die räumliche Komplexität der Inorder-Durchquerung beträgt dagegen O(1), wenn wir die Stapelgröße für Funktionsaufrufe nicht berücksichtigen. Ansonsten beträgt die räumliche Komplexität der Inorder-Durchquerung Oh), wobei „h“ die Höhe des Baumes ist.
ein Array in Java
Implementierung der Inorder-Traversierung
Sehen wir uns nun die Implementierung von Inorder-Traversal in verschiedenen Programmiersprachen an.
Programm: Schreiben Sie ein Programm zur Implementierung von Inorder-Traversal in der Sprache C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Ausgabe
Zeile vs. Spalte

Programm: Schreiben Sie ein Programm, um Inorder-Traversal in C++ zu implementieren.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Ausgabe

Programm: Schreiben Sie ein Programm zur Implementierung von Inorder-Traversal in Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Ausgabe

Das ist also alles über den Artikel. Ich hoffe, der Artikel ist hilfreich und informativ für Sie.











