A Schalter ist ein Gerät, das die Häufigkeit speichert (und manchmal anzeigt), wie oft ein bestimmtes Ereignis oder ein bestimmter Prozess aufgetreten ist, häufig in Abhängigkeit von einem Taktsignal. Zähler werden in der digitalen Elektronik zu Zählzwecken verwendet. Sie können bestimmte Ereignisse im Schaltkreis zählen. Beispielsweise erhöht ein Zähler im UP-Zähler den Zählerstand mit jeder steigenden Taktflanke. Ein Zähler kann nicht nur zählen, sondern auch einer bestimmten Sequenz folgen, die auf unserem Design basiert, wie jede beliebige Zufallssequenz 0,1,3,2…. Sie können auch mit Hilfe von Flip-Flops entworfen werden. Sie werden als Frequenzteiler verwendet, bei denen die Frequenz einer bestimmten Impulswellenform geteilt wird. Zähler sind sequentielle Schaltkreise, die die Anzahl der Impulse entweder im Binärcode oder in BCD-Form zählen. Die Haupteigenschaften eines Zählers sind Timing, Sequenzierung und Zählung. Der Zähler funktioniert in zwei Modi
Aufwärtszähler
Abwärtszähler
Gegenklassifizierung
Zähler werden grob in zwei Kategorien unterteilt
- Asynchroner Zähler
- Synchronzähler
1. Asynchroner Zähler
Bei asynchronen Zählern verwenden wir keinen Universaltakt, nur das erste Flip-Flop wird vom Haupttakt angesteuert und der Takteingang des restlichen folgenden Flip-Flops wird vom Ausgang der vorherigen Flip-Flops angesteuert. Wir können es anhand des folgenden Diagramms verstehen:
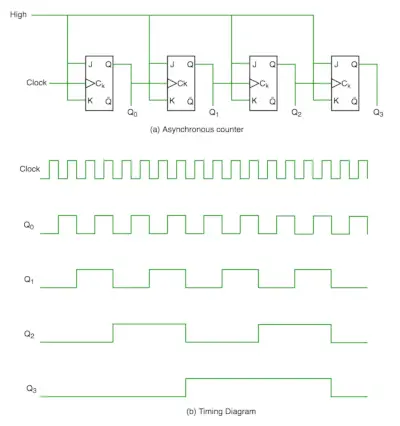
Aus dem Zeitdiagramm ist ersichtlich, dass sich Q0 ändert, sobald die steigende Flanke des Taktimpulses auftritt, Q1 sich ändert, wenn die steigende Flanke von Q0 auftritt (da Q0 wie ein Taktimpuls für das zweite Flip-Flop ist) und so weiter. Auf diese Weise werden Wellen durch Q0, Q1, Q2, Q3 erzeugt, daher wird es auch genannt RIPPLE-Zähler und Serienzähler. Ein Ripple-Zähler ist eine kaskadierte Anordnung von Flip-Flops, bei der der Ausgang eines Flip-Flops den Takteingang des folgenden Flip-Flops steuert
2. Synchroner Zähler
Im Gegensatz zum asynchronen Zähler verfügt der synchrone Zähler über einen globalen Takt, der jedes Flip-Flop antreibt, sodass sich der Ausgang parallel ändert. Der einzige Vorteil des synchronen Zählers gegenüber dem asynchronen Zähler besteht darin, dass er mit einer höheren Frequenz als der asynchrone Zähler arbeiten kann, da er keine kumulative Verzögerung aufweist, da jedem Flip-Flop der gleiche Takt gegeben wird. Er wird auch als Parallelzähler bezeichnet.
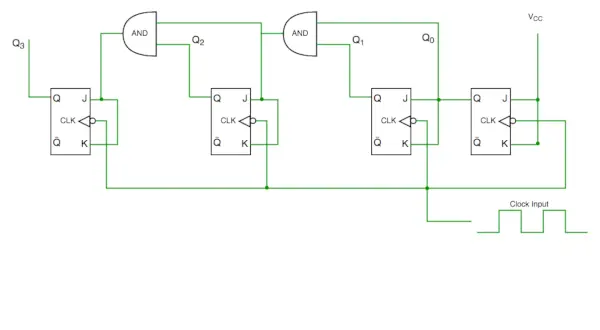
Synchrone Zählerschaltung
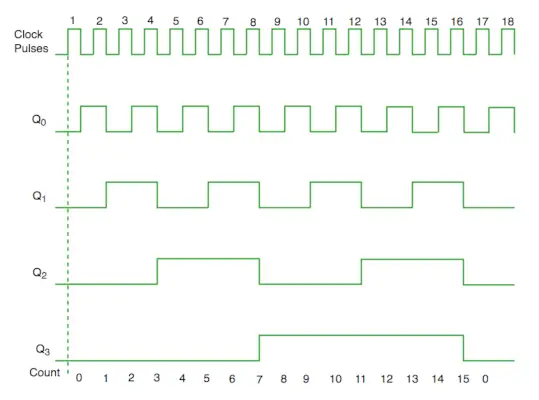
Zeitdiagramm Synchronzähler
Aus dem Schaltplan sehen wir, dass das Q0-Bit auf jede fallende Taktflanke reagiert, während Q1 von Q0, Q2 von Q1 und Q0 und Q3 von Q2, Q1 und Q0 abhängig ist.
Dekadenzähler
Ein Dekadenzähler zählt zehn verschiedene Zustände und setzt ihn dann auf seine Ausgangszustände zurück. Ein einfacher Dekadenzähler zählt von 0 bis 9, aber wir können auch Dekadenzähler erstellen, die beliebige zehn Zustände zwischen 0 und 15 durchlaufen können (für 4-Bit-Zähler).
| Taktimpuls | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Wahrheitstabelle für einfachen Dekadenzähler
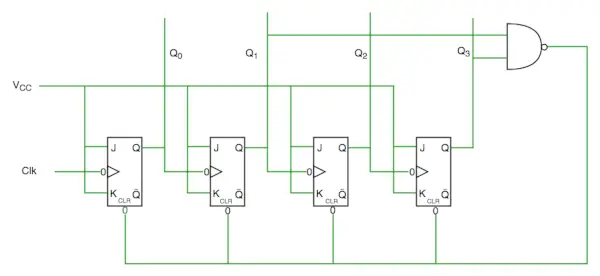
Schaltplan des Dekadenzählers
Aus dem Schaltplan können wir ersehen, dass wir ein NAND-Gatter für Q3 und Q1 verwendet und dieses in die Löscheingangsleitung eingespeist haben, da die binäre Darstellung von 10 lautet:
1010
Und wir sehen, dass Q3 und Q1 hier 1 sind. Wenn wir NAND dieser beiden Bits geben, um den Eingang zu löschen, wird der Zähler bei 10 gelöscht und beginnt wieder von vorne.
Wichtiger Punkt : Die Anzahl der im Zähler verwendeten Flip-Flops ist immer größer als gleich ( Protokoll2N ), wobei n=Anzahl der Zustände im Zähler.
Einige Gate-Fragen aus früheren Jahren zu Zählern
Q1. Betrachten Sie die teilweise Implementierung eines 2-Bit-Zählers mit T-Flip-Flops, die der Sequenz 0-2-3-1-0 folgen, wie unten gezeigt
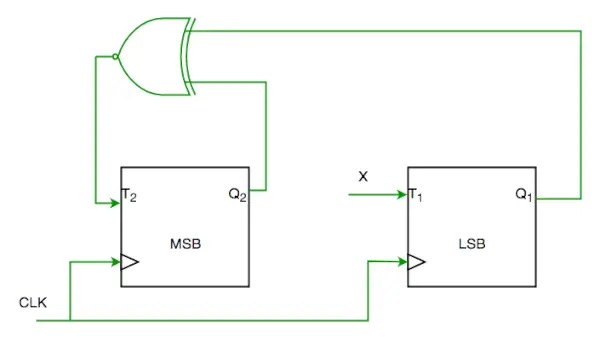
Um die Schaltung zu vervollständigen, sollte der Eingang X sein
(A) F2?
(B) Q2 + Q1
(C) (Q1 ? Q2)‘
(D) Q1 ? Q2 (GATE-CS-2004)
Lösung:
Von der Schaltung aus sehen wir
T1=XQ1’+X’Q1—-(1)
UND
T2=(Q2 ? Q1)’—-(2)
UND DER GEWÜNSCHTE AUSGANG IST 00->10->11->01->00
SO SOLLTE X SEIN Q1Q2’+Q1’Q2 ERFÜLLT 1 UND 2.
ALSO IST ANS (D) TEIL.
Q2. Die Steuersignalfunktionen eines 4-Bit-Binärzählers sind unten angegeben (wobei X egal ist).
Der Zähler wird wie folgt angeschlossen:
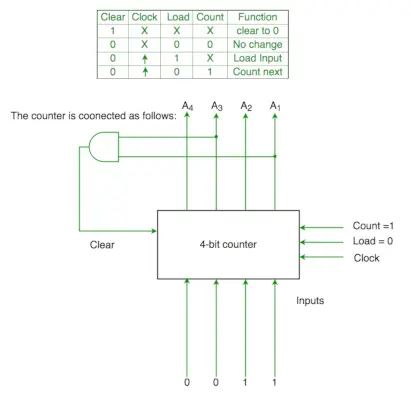
Gehen Sie davon aus, dass die Zähler- und Gate-Verzögerungen vernachlässigbar sind. Wenn der Zähler bei 0 beginnt, durchläuft er die folgende Sequenz:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (GATE-CS-2007)
Lösung:
Anfangs A1 A2 A3 A4 =0000
Clr=A1 und A3
Wenn also A1 und A3 beide 1 sind, geht es wieder auf 0000
Daher 0000(init.) -> 0001(A1 und A3=0) ->0010 (A1 und A3=0) -> 0011(A1 und A3=0) -> 0100 ( A1 und A3=1 )[ Löschbedingung erfüllt] ->0000(init.), also geht es durch 0->1->2->3->4
Ans ist (C) Teil.
String-zu-Int-Konvertierung in Java
Quiz zur digitalen Logik
Artikel von Anuj Batham,
