UNTERSCHIED ZWISCHEN DFA UND NFA - TECHCODEVIEW.COM

1. DFA: DFA bezieht sich auf Deterministic Finite Automaton. Ein endlicher Automat (FA) wird als deterministisch bezeichnet, wenn entsprechend einem Eingabesymbol ein einziger resultierender Zustand vorliegt, d. h. es nur einen Übergang gibt. Ein deterministischer endlicher Automat besteht aus fünf Tupeln, dargestellt als:

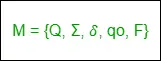
Wo,
F: Eine nicht leere endliche Menge von Zuständen in der endlichen Kontrolle (qo, q1, q2, …).
Σ: Eine nicht leere endliche Menge von Eingabesymbolen.
δ: Es handelt sich um eine Übergangsfunktion, die zwei Argumente, einen Zustand und ein Eingabesymbol, annimmt und einen einzelnen Zustand zurückgibt.
qo: Es ist der Startzustand, einer der Zustände in Q.
F: Es handelt sich um eine nicht leere Menge von Endzuständen/akzeptierenden Zuständen aus der Menge, die zu Q gehört.

2. URSACHEN:
NFA bezieht sich auf nichtdeterministische endliche Automaten. Ein endlicher Automat (FA) wird als nicht deterministisch bezeichnet, wenn es mehr als einen möglichen Übergang von einem Zustand auf demselben Eingabesymbol gibt.
Ein nichtdeterministischer endlicher Automat ist ebenfalls eine Menge von fünf Tupeln und wird dargestellt als:

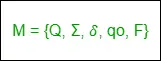
Wo,
F: Eine Menge nicht leerer endlicher Zustände.
Σ: Eine Menge nicht leerer endlicher Eingabesymbole.
δ: Es handelt sich um eine Übergangsfunktion, die einen Zustand von Q und ein Eingabesymbol von Q annimmt und eine Teilmenge von Q zurückgibt.
qo: Ausgangszustand der NFA und Mitglied von Q.
F: Eine nicht leere Menge von Endzuständen und Mitglied von Q.

Voraussetzung – Automatisch fertig

Unterschied zwischen DFA und NFA:

DFA	NFA
DFA steht für Deterministic Finite Automata.	NFA steht für Nondeterministic Finite Automata.
Für jede symbolische Darstellung des Alphabets gibt es in DFA nur einen Zustandsübergang.	Es ist nicht erforderlich, anzugeben, wie die NFA auf ein bestimmtes Symbol reagiert.
DFA kann den Übergang „Leere Zeichenfolge“ nicht verwenden.	NFA kann den Übergang „Leere Zeichenfolge“ verwenden.
DFA kann als eine Maschine verstanden werden.	Unter NFA kann man verstehen, dass mehrere kleine Maschinen gleichzeitig arbeiten.
In DFA wird der nächstmögliche Zustand eindeutig festgelegt.	In NFA kann jedes Paar aus Zustand und Eingabesymbol viele mögliche nächste Zustände haben.
DFA ist schwieriger zu konstruieren.	NFA ist einfacher zu konstruieren.
DFA lehnt die Zeichenfolge ab, falls sie in einem anderen Status als dem akzeptierenden Status endet.	NFA lehnt die Zeichenfolge ab, wenn alle Zweige ausfallen oder die Zeichenfolge ablehnen.
Die zum Ausführen einer Eingabezeichenfolge benötigte Zeit ist kürzer.	Die zum Ausführen einer Eingabezeichenfolge benötigte Zeit ist länger.
Alle DFA sind NFA.	Nicht alle NFA sind DFA.
DFA benötigt mehr Platz.	NFA benötigt weniger Platz als DFA.
Eine tote Konfiguration ist nicht zulässig. Beispiel: Wenn wir den q0-Zustand als Eingabe 0 angeben, müssen wir als Selbstschleife 1 als Eingabe an q0 übergeben.	Eine tote Konfiguration ist zulässig. Beispiel: Wenn wir den Eingang q0 als 0 eingeben, können wir als nächsten Eingang 1 an q1 eingeben, der zum nächsten Zustand wechselt.
δ: QxΣ -> Q, d. h. der nächste mögliche Zustand gehört zu Q.	δ: Qx(Σ U ε) -> 2^Q, d. h. der nächste mögliche Zustand gehört zur Potenzmenge von Q.
Backtracking ist in DFA zulässig.	Ein Zurückverfolgen ist in NFA nicht immer möglich.
Die Konvertierung von regulären Ausdrücken in DFA ist schwierig.	Die Konvertierung von regulären Ausdrücken in NFA ist im Vergleich zu DFA einfacher.
Epsilon-Verschiebungen sind in DFA nicht zulässig	Epsilon-Verschiebung ist in NFA erlaubt
DFA erlaubt nur einen Zug für ein einzelnes Eingabealphabet.	Es kann eine Auswahlmöglichkeit (mehr als ein Zug) für ein einzelnes Eingabealphabet bestehen.