Endliche Automaten (FA) sind die einfachste Maschine zum Erkennen von Mustern. Sie werden zur Charakterisierung einer regulären Sprache verwendet, zum Beispiel: /baa+!/.
Außerdem wird es zum Analysieren und Erkennen natürlichsprachlicher Ausdrücke verwendet. Der endliche Automat oder die endliche Zustandsmaschine ist eine abstrakte Maschine mit fünf Elementen oder Tupeln. Es verfügt über eine Reihe von Zuständen und Regeln für den Übergang von einem Zustand in einen anderen, hängt jedoch vom verwendeten Eingabesymbol ab. Basierend auf den Zuständen und dem Regelwerk kann die Eingabezeichenfolge entweder akzeptiert oder abgelehnt werden. Im Grunde handelt es sich um ein abstraktes Modell eines digitalen Computers, der eine Eingabezeichenfolge liest und seinen internen Zustand abhängig vom aktuellen Eingabesymbol ändert. Jeder Automat definiert eine Sprache, d. h. eine Reihe von Zeichenfolgen, die er akzeptiert. Die folgende Abbildung zeigt einige wesentliche Merkmale der allgemeinen Automatisierung.
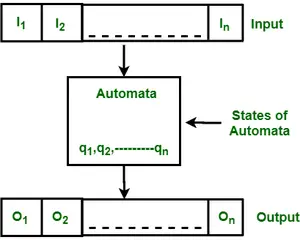
Figur: Merkmale endlicher Automaten
Die obige Abbildung zeigt die folgenden Merkmale von Automaten:
- Eingang
- Ausgabe
- Zustände von Automaten
- Staatsbeziehung
- Ausgabebeziehung
Ein endlicher Automat besteht aus Folgendem:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Formale Spezifikation der Maschine ist
string.replaceall Java
{ Q, ?, q, F, ? }> FA wird in zwei Typen charakterisiert:
1) Deterministische endliche Automaten (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->F.> Bei einem DFA wechselt die Maschine für ein bestimmtes Eingabezeichen nur in einen Zustand. Für jeden Zustand wird für jedes Eingabesymbol eine Übergangsfunktion definiert. Auch in DFA ist das Verschieben von Nullen (oder ?) nicht zulässig, d. h. DFA kann den Status nicht ohne Eingabezeichen ändern.
Erstellen Sie beispielsweise einen DFA, der eine Sprache aller Zeichenfolgen akzeptiert, die mit „a“ enden.
Gegeben: ? = {a,b}, q = {q0}, F={q1}, Q = {q0, Q1}
String-Format Java
Betrachten Sie zunächst einen Sprachsatz aller möglichen akzeptablen Zeichenfolgen, um ein genaues Zustandsübergangsdiagramm zu erstellen.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, Vater, Vater, Vater, Vater}
Oben ist eine einfache Teilmenge der möglichen akzeptablen Zeichenfolgen. Es gibt viele andere Zeichenfolgen, die mit „a“ enden und die Symbole {a,b} enthalten.
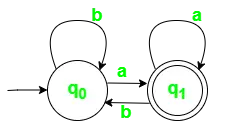
Abb. 1. Zustandsübergangsdiagramm für DFA mit ? = {a, b}
Nicht akzeptierte Zeichenfolgen sind:
ab, bb, aab, abbb usw.
Zustandsübergangstabelle für den oben genannten Automaten,
| ?ZustandSymbol? | A | B |
|---|---|---|
| Q0 | Q1 | Q0 |
| Q1 | Q1 | Q0 |
Eine wichtige Sache, die es zu beachten gilt, ist: Es kann viele mögliche DFAs für ein Muster geben . Im Allgemeinen wird ein DFA mit einer Mindestanzahl an Staaten bevorzugt.
2) Nichtdeterministische endliche Automaten (NFA): NFA ähnelt DFA mit Ausnahme der folgenden zusätzlichen Funktionen:
So finden Sie versteckte Dinge auf Android
- Eine Nullbewegung (oder ?) ist zulässig, d. h. es kann vorwärts bewegt werden, ohne dass Symbole gelesen werden müssen.
- Möglichkeit zur Übertragung in eine beliebige Anzahl von Zuständen für einen bestimmten Eingang.
Diese oben genannten Funktionen verleihen NFA jedoch keine zusätzliche Leistung. Wenn wir beide hinsichtlich der Leistung vergleichen, sind beide gleichwertig.
MySQL nicht gleich
Aufgrund der oben genannten zusätzlichen Funktionen verfügt NFA über eine andere Übergangsfunktion, der Rest ist der gleiche wie DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ F.>
Wie Sie sehen können, gilt die Übergangsfunktion für jede Eingabe, einschließlich Null (oder ?), NFA kann in einen beliebigen Zustand mit einer beliebigen Anzahl von Zuständen wechseln. Nachfolgend finden Sie beispielsweise eine NFA für das oben genannte Problem.
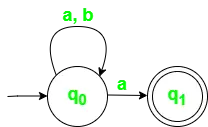
Abb. 2. Zustandsübergangsdiagramm für NFA mit ? = {a, b}
Zustandsübergangstabelle für den oben genannten Automaten,
| ?ZustandSymbol? | A | B |
|---|---|---|
| Q0 | {Q0,Q1} | Q0 |
| Q1 | ? | ? |
Eine wichtige Sache, die es zu beachten gilt, ist: Wenn in NFA ein Pfad für eine Eingabezeichenfolge zu einem Endzustand führt, dann die Eingabezeichenfolge Ist akzeptiert . Beispielsweise gibt es im obigen NFA mehrere Pfade für die Eingabezeichenfolge 00. Da einer der Pfade zu einem Endzustand führt, wird 00 vom obigen NFA akzeptiert.
Einige wichtige Punkte:
- Rechtfertigung:
In case of DFA ? : Q X ? -->F Im Falle von NFA? : Q X ? --> 2Q>
Wenn Sie nun beobachten, finden Sie Q X heraus? –> Q ist Teil von Q X ? –> 2Q.
Scanner in Java
Auf der RHS-Seite ist Q die Teilmenge von 2Qwas darauf hinweist, dass Q in 2 enthalten istQoder Q ist ein Teil von 2QDas Gegenteil ist jedoch nicht der Fall. Mathematisch können wir daraus schließen Jeder DFA ist NFA, aber nicht umgekehrt . Dennoch gibt es eine Möglichkeit, eine NFA in eine DFA umzuwandeln Für jeden NFA gibt es einen entsprechenden DFA .
- Sowohl NFA als auch DFA haben die gleiche Macht und jeder NFA kann in einen DFA übersetzt werden.
- Sowohl in DFA als auch in NFA kann es mehrere Endzustände geben.
- NFA ist eher ein theoretisches Konzept.
- DFA wird in der lexikalischen Analyse im Compiler verwendet.
- Wenn die Anzahl der Staaten in der NFA N beträgt, kann die DFA maximal 2 habenNAnzahl der Staaten.
Siehe Quiz zu regulären Ausdrücken und endlichen Automaten.
