Ein Encoder ist eine digitale Schaltung, die eine Reihe binärer Eingänge in einen eindeutigen Binärcode umwandelt. Der Binärcode stellt die Position des Eingangs dar und wird verwendet, um den spezifischen Eingang zu identifizieren, der aktiv ist. Encoder werden üblicherweise in digitalen Systemen verwendet, um einen parallelen Satz von Eingaben in einen seriellen Code umzuwandeln.
Das Grundprinzip eines Encoders besteht darin, jedem möglichen Eingang einen eindeutigen Binärcode zuzuweisen. Beispielsweise verfügt ein 2-zu-4-Zeilen-Encoder über 2 Eingangsleitungen und 4 Ausgangsleitungen und weist jeder der 2^2 = 4 möglichen Eingangskombinationen einen eindeutigen 4-Bit-Binärcode zu. Der Ausgang eines Encoders ist normalerweise aktiv niedrig, was bedeutet, dass jeweils nur ein Ausgang aktiv (niedrig) ist und die übrigen Ausgänge inaktiv (hoch) sind. Der aktive Low-Ausgang wird basierend auf dem Binärcode ausgewählt, der dem aktiven Eingang zugewiesen ist.
Es gibt verschiedene Arten von Encodern, darunter Prioritätsencoder, die jedem Eingang eine Priorität zuweisen, und binär gewichtete Encoder, die ein binäres Gewichtungssystem verwenden, um Binärcodes den Eingängen zuzuweisen. Zusammenfassend ist ein Encoder eine digitale Schaltung, die eine Reihe binärer Eingaben in einen eindeutigen Binärcode umwandelt, der die Position der Eingabe darstellt. Encoder werden in digitalen Systemen häufig verwendet, um parallele Eingaben in serielle Codes umzuwandeln.
Ein Encoder ist ein Kombinationsschaltung das die umgekehrte Operation von a durchführt Decoder . Es hat maximal 2^n Eingabezeilen Und 'n' Ausgabezeilen Daher kodiert es die Informationen von 2^n Eingaben in einen n-Bit-Code. Es wird ein Binärcode erzeugt, der dem Eingang entspricht, der aktiv High ist. Daher codiert der Encoder 2^n Eingangsleitungen mit „n“ Bits.
Encoder
Arten von Encodern
Es gibt verschiedene Arten von Encodern, die unten aufgeführt sind.
- 4 zu 2 Encoder
- Oktal-zu-Binär-Encoder (8 zu 3 Encoder)
- Dezimal-zu-BCD-Encoder
- Prioritäts-Encoder
4 zu 2 Encoder
Der 4-zu-2-Encoder besteht aus vier Eingänge Y3, Y2, Y1 und Y0 und zwei Ausgänge A1 und A0 . Es darf immer nur einer dieser 4 Eingänge „1“ sein, um am Ausgang den entsprechenden Binärcode zu erhalten. Die folgende Abbildung zeigt das Logiksymbol des 4-zu-2-Encoders.
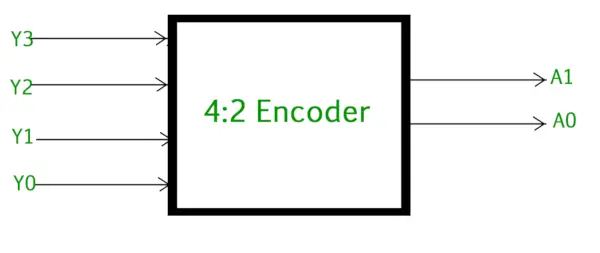
4 zu 2 Encoder
Die Wahrheitstabelle von 4 zu 2 Encodern sieht wie folgt aus.
| EINGÄNGE | AUSGÄNGE | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Logischer Ausdruck für A1 und A0:
A1 = Y3 + Y2 A0 = Y3 + Y1>
Die beiden oben genannten booleschen Funktionen A1 und A0 können mithilfe von zwei Eingangs-OR-Gattern implementiert werden:
int zum Stringen in Java
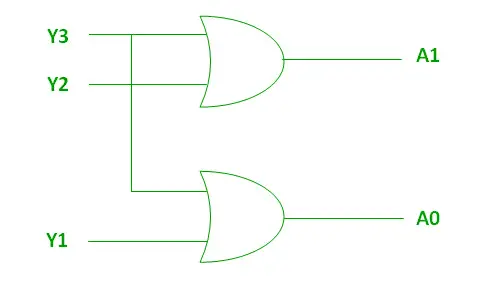
Umsetzung mittels OR-Gate
Beziehungszusammensetzung
Oktal-zu-Binär-Encoder (8 zu 3 Encoder)
Der 8-zu-3-Encoder oder Oktal-zu-Binär-Encoder besteht aus 8 Eingänge : Y7 bis Y0 und 3 Ausgänge : A2, A1 und A0. Jede Eingangsleitung entspricht jeder Oktalziffer und drei Ausgänge erzeugen den entsprechenden Binärcode. Die folgende Abbildung zeigt das Logiksymbol von Oktal zu Binärkodierer.
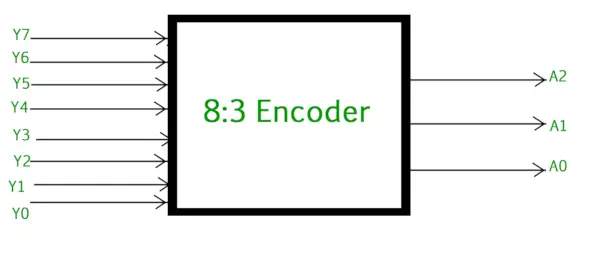
Oktal-zu-Binär-Encoder (8 zu 3 Encoder)
Die Wahrheitstabelle für den 8-zu-3-Encoder lautet wie folgt.
| EINGÄNGE | AUSGÄNGE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Logischer Ausdruck für A2, A1 und A0.
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
Die beiden oben genannten booleschen Funktionen A2, A1 und A0 können mit vier Eingaben implementiert werden ODER-Tore .
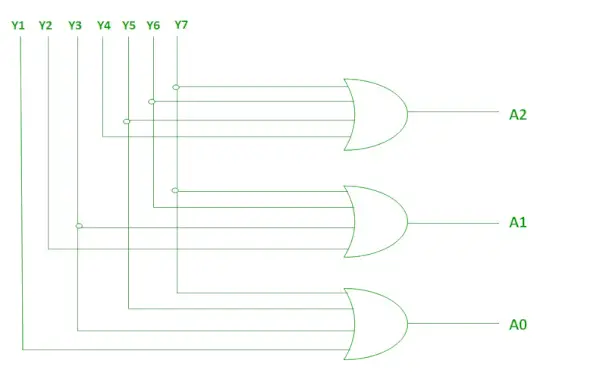
Umsetzung mittels OR-Gate
Dezimal-zu-BCD-Encoder
Der Dezimal-zu-Binär-Encoder besteht normalerweise aus 10 Eingabezeilen Und 4 Ausgangsleitungen . Jede Eingabezeile entspricht jeder Dezimalstelle und 4 Ausgänge entsprechen dem BCD-Code. Dieser Encoder akzeptiert die dekodierten Dezimaldaten als Eingabe und kodiert sie in den BCD-Ausgang, der auf den Ausgangsleitungen verfügbar ist. Die folgende Abbildung zeigt das Logiksymbol des Dezimal-zu-BCD-Encoders:
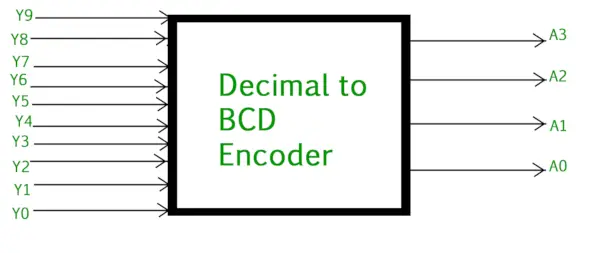
Dezimal-zu-BCD-Encoder
Die Wahrheitstabelle für Dezimalzahl bis BCD-Encoder ist wie folgt.
| EINGÄNGE | AUSGÄNGE | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | Y8 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Logischer Ausdruck für A3, A2, A1 und A0.
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
Die beiden oben genannten booleschen Funktionen können mithilfe von ODER-Gattern implementiert werden.
Java-Einfügungssortierung
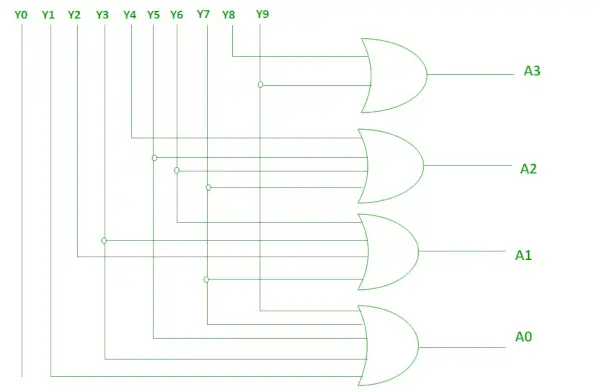
Umsetzung mittels OR-Gate
Prioritäts-Encoder
Ein 4-zu-2-Prioritätsencoder verfügt über 4 Eingänge : Y3, Y2, Y1 & Y0 und 2 Ausgänge : A1 & A0. Hier hat der Eingang Y3 den höchste Priorität , wohingegen die Eingabe Y0 die hat niedrigste Priorität . Selbst wenn in diesem Fall mehr als eine Eingabe gleichzeitig „1“ ist, ist die Ausgabe der (Binär-)Code, der der Eingabe entspricht, die vorliegt Höhere Priorität . Die Wahrheitstabelle für den Prioritätsencoder lautet wie folgt.
| EINGÄNGE | AUSGÄNGE | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | IN |
| 0 | 0 | 0 | 0 | X | X | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
Der logische Ausdruck für A1 ist unten dargestellt.
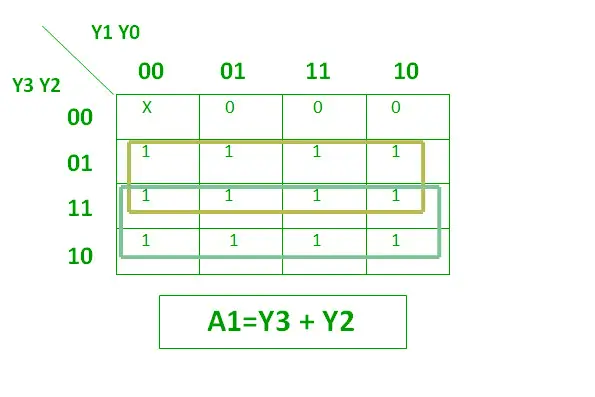
Logischer Ausdruck
Der logische Ausdruck für A0 ist unten dargestellt.
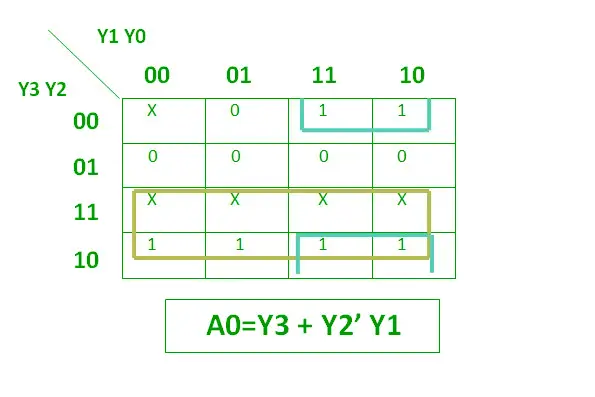
Logischer Ausdruck
Die beiden oben genannten booleschen Funktionen können als implementiert werden.
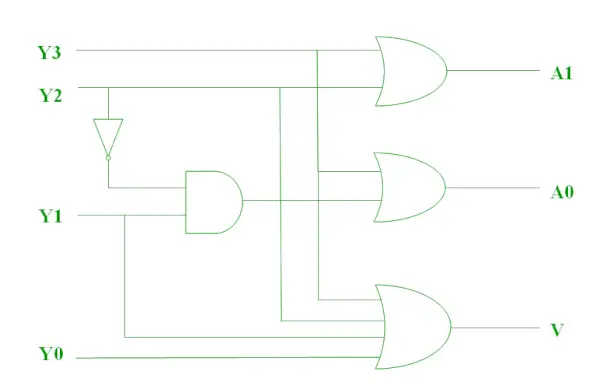
Prioritäts-Encoder
Es gibt einige Fehler, die normalerweise bei Encodern auftreten, die unten aufgeführt sind.
- Eine Mehrdeutigkeit liegt vor, wenn alle Ausgänge des Encoders gleich Null sind.
- Wenn mehr als ein Eingang aktiv High ist, erzeugt der Encoder einen Ausgang, der möglicherweise nicht den richtigen Code hat.
Um diese Schwierigkeiten zu überwinden, sollten wir jedem Eingang des Encoders Prioritäten zuweisen. Dann ist der Ausgang des Encoders der Code, der den aktiven High-Eingängen entspricht, die eine höhere Priorität haben.
Anwendung von Encodern
- Encoder sind weit verbreitete elektronische Schaltkreise, die in allen digitalen Systemen verwendet werden.
- Encoder werden verwendet, um die Dezimalwerte in Binärwerte umzuwandeln, um Binärfunktionen wie Addition, Subtraktion, Multiplikation usw. auszuführen.
- Andere Anwendungen, insbesondere für Prioritätsencoder, können die Erkennung von Interrupts in Mikroprozessoranwendungen umfassen.
Vorteile der Verwendung von Encodern in der digitalen Logik
- Reduzierung der Zeilenanzahl: Encoder reduzieren die Anzahl der Leitungen, die zur Übertragung von Informationen von mehreren Eingängen an einen einzelnen Ausgang erforderlich sind, was den Entwurf des Systems vereinfachen und die Kosten für Komponenten senken kann.
- Verbesserte Zuverlässigkeit: Durch die Umwandlung mehrerer Eingaben in einen einzigen seriellen Code können Encoder die Möglichkeit von Fehlern bei der Informationsübertragung reduzieren.
- Verbesserte Leistung: Encoder können die Leistung eines digitalen Systems verbessern, indem sie die Zeit reduzieren, die für die Übertragung von Informationen von mehreren Eingängen an einen einzelnen Ausgang erforderlich ist.
Nachteile der Verwendung von Encodern in der digitalen Logik
- Erhöhte Komplexität: Encoder sind im Vergleich zu typischerweise komplexere Schaltkreise Multiplexer und erfordern für die Implementierung zusätzliche Komponenten.
- Auf bestimmte Anwendungen beschränkt: Encoder eignen sich nur für Anwendungen, bei denen ein paralleler Satz von Eingängen in einen seriellen Code umgewandelt werden muss.
- Eingeschränkte Flexibilität: Encoder sind in ihrer Flexibilität eingeschränkt, da sie nur eine feste Anzahl von Eingaben in eine feste Anzahl von Ausgaben kodieren können.
- Zusammenfassend lässt sich sagen, dass Encoder nützliche digitale Schaltkreise sind, die ihre Vor- und Nachteile haben. Die Entscheidung, ob ein Encoder verwendet wird oder nicht, hängt von den spezifischen Anforderungen des Systems und den Kompromissen zwischen Komplexität, Zuverlässigkeit, Leistung und Kosten ab.
Fragen zur GATE CS-Ecke
Das Üben der folgenden Fragen wird Ihnen helfen, Ihr Wissen zu testen. Alle Fragen wurden in den vergangenen Jahren in GATE oder in GATE Mock Tests gestellt. Es wird dringend empfohlen, sie zu üben.
- GATE CS 2013, Frage 65
- GATE CS 2014 (Satz 3), Frage 65
