Bei einem Gitter von Zahlen finden Sie eine maximale Länge Schlangensequenz und drucken Sie sie. Wenn mehrere Schlangensequenzen mit der maximalen Länge existieren, drucken Sie eine davon.
Eine Schlangensequenz besteht aus benachbarten Zahlen im Raster, so dass für jede Zahl die Nummer rechts oder die darunter liegende Zahl +1 oder -1 ihr Wert beträgt. Wenn Sie beispielsweise im Raster am Standort (x y) sind, können Sie sich entweder rechts bewegen, d. H. (x y+1) Wenn diese Zahl ± 1 ist oder sich nach unten bewegen, d. H. (x+1 y), wenn diese Zahl ± 1 ist.
For example 9 6 5 2 8 7 6 5 7 3 1 6 1 1 1 7 In above grid the longest snake sequence is: (9 8 7 6 5 6 7)
Die folgende Abbildung zeigt alle möglichen Pfade:
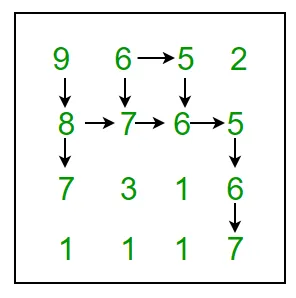
Wir empfehlen Ihnen dringend, Ihren Browser zu minimieren und dies zuerst selbst zu versuchen.
Die Idee ist, dynamische Programmierung zu verwenden. Für jede Zelle der Matrix halten wir die maximale Länge einer Schlange, die in der Stromzelle endet. Die Schlangensequenz der maximalen Länge hat einen maximalen Wert. Die maximale Wertzelle entspricht dem Schwanz der Schlange. Um die Schlange zu drucken, müssen wir den Schwanz bis zum Kopf von Snake zurückverfolgen.
Let T[i][i] represent maximum length of a snake which ends at cell (i j) then for given matrix M the DP relation is defined as T[0][0] = 0 T[i][j] = max(T[i][j] T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1 T[i][j] = max(T[i][j] T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Nachfolgend finden Sie die Implementierung der Idee
C++// C++ program to find maximum length // Snake sequence and print it #include
// Java program to find maximum length // Snake sequence and print it import java.util.*; class GFG { static int M = 4; static int N = 4; static class Point { int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int grid[][] int mat[][] int i int j) { List<Point> path = new LinkedList<>(); Point pt = new Point(i j); path.add(0 pt); while (grid[i][j] != 0) { if (i > 0 && grid[i][j] - 1 == grid[i - 1][j]) { pt = new Point(i - 1 j); path.add(0 pt); i--; } else if (j > 0 && grid[i][j] - 1 == grid[i][j - 1]) { pt = new Point(i j - 1); path.add(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int mat[][]) { // table to store results of subproblems int [][]lookup = new int[M][N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.abs(mat[i - 1][j] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i - 1][j] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.abs(mat[i][j - 1] - mat[i][j]) == 1) { lookup[i][j] = Math.max(lookup[i][j] lookup[i][j - 1] + 1); if (max_len < lookup[i][j]) { max_len = lookup[i][j]; max_row = i; max_col = j; } } } } } System.out.print('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); System.out.print('Snake sequence is:'); for (Point it : path) System.out.print('n' + mat[it.x][it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void main(String[] args) { int mat[][] = {{9 6 5 2} {8 7 6 5} {7 3 1 6} {1 1 1 7}}; findSnakeSequence(mat); } } // This code is contributed by 29AjayKumar
// C# program to find maximum length // Snake sequence and print it using System; using System.Collections.Generic; class GFG { static int M = 4; static int N = 4; public class Point { public int x y; public Point(int x int y) { this.x = x; this.y = y; } }; // Function to find maximum length Snake sequence path // (i j) corresponds to tail of the snake static List<Point> findPath(int[ ] grid int[ ] mat int i int j) { List<Point> path = new List<Point>(); Point pt = new Point(i j); path.Insert(0 pt); while (grid[i j] != 0) { if (i > 0 && grid[i j] - 1 == grid[i - 1 j]) { pt = new Point(i - 1 j); path.Insert(0 pt); i--; } else if (j > 0 && grid[i j] - 1 == grid[i j - 1]) { pt = new Point(i j - 1); path.Insert(0 pt); j--; } } return path; } // Function to find maximum length Snake sequence static void findSnakeSequence(int[ ] mat) { // table to store results of subproblems int[ ] lookup = new int[M N]; // initialize by 0 // stores maximum length of Snake sequence int max_len = 0; // store coordinates to snake's tail int max_row = 0; int max_col = 0; // fill the table in bottom-up fashion for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { // do except for (0 0) cell if (i != 0 || j != 0) { // look above if (i > 0 && Math.Abs(mat[i - 1 j] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i - 1 j] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } // look left if (j > 0 && Math.Abs(mat[i j - 1] - mat[i j]) == 1) { lookup[i j] = Math.Max( lookup[i j] lookup[i j - 1] + 1); if (max_len < lookup[i j]) { max_len = lookup[i j]; max_row = i; max_col = j; } } } } } Console.Write('Maximum length of Snake ' + 'sequence is: ' + max_len + 'n'); // find maximum length Snake sequence path List<Point> path = findPath(lookup mat max_row max_col); Console.Write('Snake sequence is:'); foreach(Point it in path) Console.Write('n' + mat[it.x it.y] + ' (' + it.x + ' ' + it.y + ')'); } // Driver code public static void Main(String[] args) { int[ ] mat = { { 9 6 5 2 } { 8 7 6 5 } { 7 3 1 6 } { 1 1 1 7 } }; findSnakeSequence(mat); } } // This code is contributed by Princi Singh
def snakesequence(S m n): sequence = {} DP = [[1 for x in range(m+1)] for x in range(n+1)] a b maximum = 0 0 0 position = [0 0] for i in range(0 n+1): for j in range(0 m+1): a b = 0 0 p = 'initial' if(i > 0 and abs(S[i][j] - S[i-1][j]) == 1): a = DP[i-1][j] if(j > 0 and abs(S[i][j] - S[i][j-1]) == 1): b = DP[i][j-1] if a != 0 and a >= b: p = str(i-1) + ' ' + str(j) elif b != 0: p = str(i) + ' ' + str(j-1) q = str(i) + ' ' + str(j) sequence[q] = p DP[i][j] = DP[i][j] + max(a b) if DP[i][j] >= maximum: maximum = DP[i][j] position[0] = i position[1] = j snakeValues = [] snakePositions = [] snakeValues.append(S[position[0]][position[1]]) check = 'found' str_next = str(position[0]) + ' ' + str(position[1]) findingIndices = sequence[str_next].split() while(check == 'found'): if sequence[str_next] == 'initial': snakePositions.insert(0 str_next) check = 'end' continue findingIndices = sequence[str_next].split() g = int(findingIndices[0]) h = int(findingIndices[1]) snakeValues.insert(0 S[g][h]) snake_position = str(g) + ' ' + str(h) snakePositions.insert(0 str_next) str_next = sequence[str_next] return [snakeValues snakePositions] S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] m = 3 n = 3 seq = snakesequence(S m n) for i in range(len(seq[0])): print(seq[0][i] '' seq[1][i].split())
function snakesequence(S m n) { let sequence = {} let DP = new Array(n + 1) for (var i = 0; i <= n; i++) DP[i] = new Array(m + 1).fill(1) let a = 0 b = 0 maximum = 0 let position = [0 0] for (var i = 0; i <= n; i++) { for (var j = 0; j <= m; j++) { a = 0 b = 0 let p = 'initial' if(i > 0 && Math.abs(S[i][j] - S[i-1][j]) == 1) a = DP[i-1][j] if(j > 0 && Math.abs(S[i][j] - S[i][j-1]) == 1) b = DP[i][j-1] if (a != 0 && a >= b) p = String(i-1) + ' ' + String(j) else if (b != 0) p = String(i) + ' ' + String(j-1) let q = String(i) + ' ' + String(j) sequence[q] = p DP[i][j] = DP[i][j] + Math.max(a b) if (DP[i][j] >= maximum) { maximum = DP[i][j] position[0] = i position[1] = j } } } let snakeValues = [] let snakePositions = [] snakeValues.push(S[position[0]][position[1]]) let check = 'found' let String_next = String(position[0]) + ' ' + String(position[1]) let findingIndices = sequence[String_next].split(' ') while(check == 'found') { if (sequence[String_next] == 'initial') { snakePositions.unshift(String_next) check = 'end' continue } findingIndices = sequence[String_next].split(' ') let g = parseInt(findingIndices[0]) let h = parseInt(findingIndices[1]) snakeValues.unshift(S[g][h]) let snake_position = String(g) + ' ' + String(h) snakePositions.unshift(String_next) String_next = sequence[String_next] } return [snakeValues snakePositions] } // Driver Code let S = [[9 6 5 2] [8 7 6 5] [7 3 1 6] [1 1 10 7]] let m = 3 let n = 3 let seq = snakesequence(S m n) for (var i = 0; i < seq[0].length; i++) console.log(seq[0][i] + '' seq[1][i].split(' '))
Ausgabe
Maximum length of Snake sequence is: 6 Snake sequence is: 9 (0 0) 8 (1 0) 7 (1 1) 6 (1 2) 5 (1 3) 6 (2 3) 7 (3 3)
Die Zeitkomplexität der obigen Lösung ist O (M*n). Hilfsraum, die von der obigen Lösung verwendet wird, ist O (M*n). Wenn wir nicht zum Drucken des Schlangenraums verpflichtet sind, kann der Schlangenraum weiter auf o (n) reduziert werden, da wir das Ergebnis aus der letzten Zeile nur verwenden.
