In diesem Artikel werden wir die Postorder-Traversierung in der Datenstruktur diskutieren.
Lineare Datenstrukturen wie Stapel, Array, Warteschlange usw. haben nur eine Möglichkeit, die Daten zu durchlaufen. Aber in einer hierarchischen Datenstruktur wie z Baum Es gibt mehrere Möglichkeiten, die Daten zu durchlaufen. Daher werden wir hier eine andere Möglichkeit zum Durchlaufen der Baumdatenstruktur diskutieren, d. h. Versandhandel . Die Postorder-Traversierung ist eine der Traversierungstechniken, die zum Besuch des Knotens im Baum verwendet wird. Es folgt dem Prinzip LRN (Links-Rechts-Knoten) . Postorder-Traversal wird verwendet, um den Postfix-Ausdruck eines Baums zu erhalten.
Die folgenden Schritte werden verwendet, um die Postorder-Traversierung durchzuführen:
- Durchlaufen Sie den linken Teilbaum, indem Sie die Postorder-Funktion rekursiv aufrufen.
- Durchlaufen Sie den rechten Teilbaum, indem Sie die Postorder-Funktion rekursiv aufrufen.
- Greifen Sie auf den Datenteil des aktuellen Knotens zu.
Die Post-Order-Traversal-Technik folgt dem Links-Rechts-Wurzel Politik. Hier bedeutet Left Right Root, dass zuerst der linke Teilbaum des Wurzelknotens durchlaufen wird, dann der rechte Teilbaum und schließlich der Wurzelknoten. Hier deutet der Postorder-Name selbst darauf hin, dass der Wurzelknoten des Baums zuletzt durchlaufen wird.
Algorithmus
Sehen wir uns nun den Algorithmus der Postorder-Traversierung an.
Step 1: Repeat Steps 2 to 4 while TREE != NULL Step 2: POSTORDER(TREE -> LEFT) Step 3: POSTORDER(TREE -> RIGHT) Step 4: Write TREE -> DATA [END OF LOOP] Step 5: END
Beispiel einer Versandhandelsdurchquerung
Sehen wir uns nun ein Beispiel für Postorder-Traversal an. Anhand eines Beispiels lässt sich der Prozess der Postorder-Traversierung leichter verstehen.
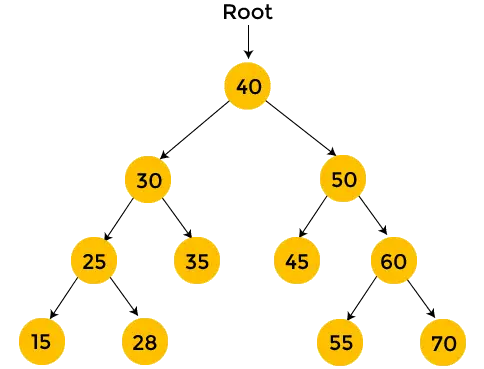
Die Knoten mit gelber Farbe wurden noch nicht besucht. Jetzt werden wir die Knoten des obigen Baums mithilfe der Postorder-Traversierung durchlaufen.
- Hier ist 40 der Wurzelknoten. Wir besuchen zunächst den linken Teilbaum von 40, also 30. Knoten 30 wird ebenfalls in der Post-Reihenfolge durchlaufen. 25 ist der linke Teilbaum von 30 und wird daher auch in der Post-Reihenfolge durchlaufen. Dann ist 15 der linke Teilbaum von 25. Aber 15 hat keinen Teilbaum, also Drucken 15 und bewegen Sie sich zum rechten Teilbaum von 25.
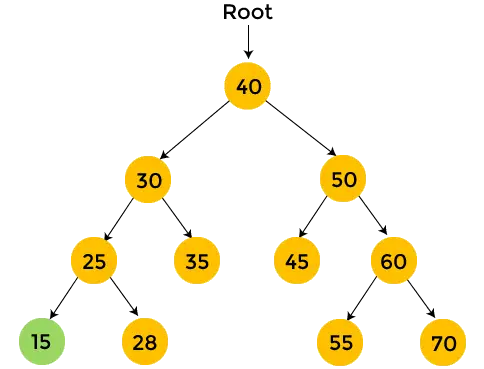
- 28 ist der rechte Teilbaum von 25 und hat keine Kinder. Also, Drucken 28 .
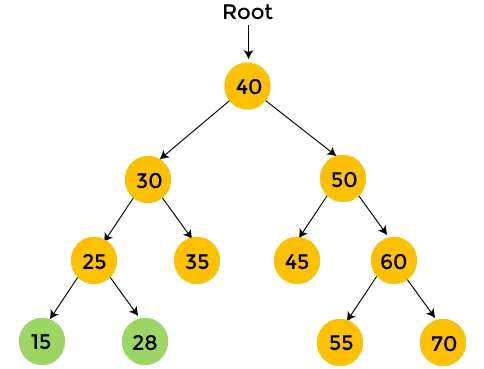
- Jetzt, Drucken 25 und die Postorder-Traversierung für 25 ist fertig.
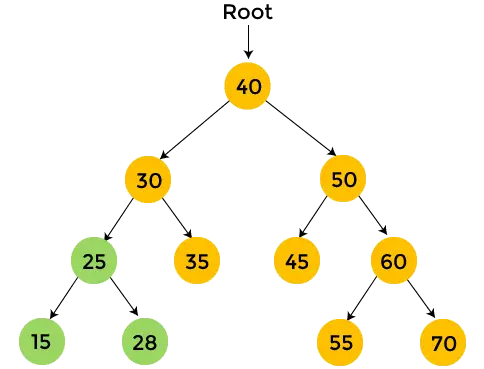
- Gehen Sie als Nächstes zum rechten Teilbaum von 30. 35 ist der rechte Teilbaum von 30 und hat keine untergeordneten Elemente. Also, Drucken 35 .
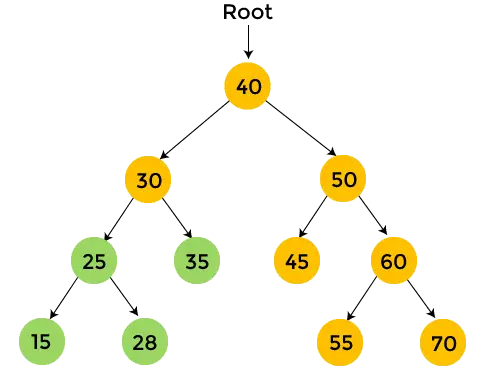
- Danach, Drucken 30 und die Postorder-Traversierung für 30 ist fertig. Es wird also der linke Teilbaum des gegebenen Binärbaums durchlaufen.
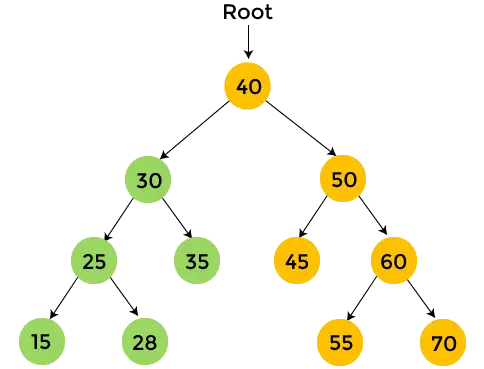
- Bewegen Sie sich nun zum rechten Teilbaum von 40, also 50, und er wird auch in der Post-Reihenfolge durchlaufen. 45 ist der linke Teilbaum von 50 und hat keine untergeordneten Elemente. Also, Drucken 45 und bewegen Sie sich zum rechten Teilbaum von 50.
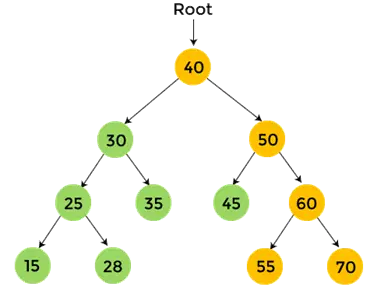
- 60 ist der rechte Teilbaum von 50, der auch in der Nachbestellung durchlaufen wird. 55 ist der linke Teilbaum von 60, der keine Kinder hat. Also, Drucken 55 .
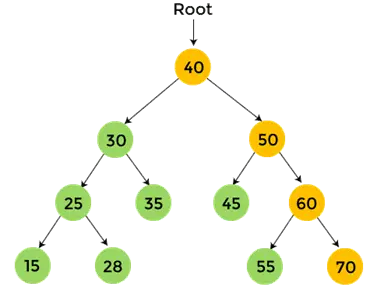
- Jetzt, Druck 70, Das ist der rechte Teilbaum von 60.
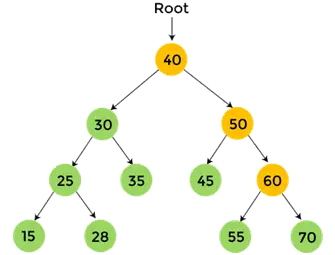
- Jetzt, Druck 60, und der Post-Order-Durchlauf für 60 ist abgeschlossen.
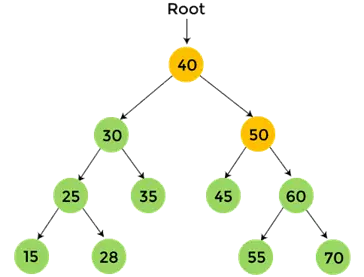
- Jetzt, 50 drucken, und der Post-Order-Durchlauf für 50 ist abgeschlossen.
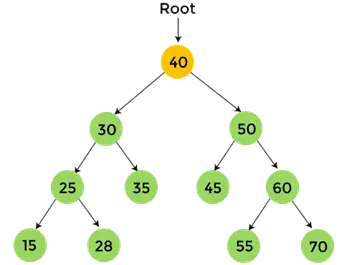
- Zu guter Letzt, Druck 40, Dies ist der Wurzelknoten des angegebenen Binärbaums, und die Post-Order-Traversierung für Knoten 40 ist abgeschlossen.
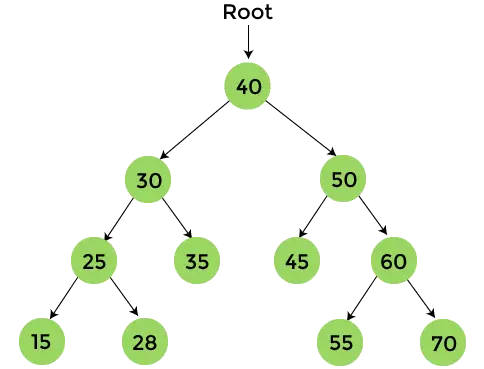
Die endgültige Ausgabe, die wir nach der Postorder-Durchquerung erhalten, ist –
{15, 28, 25, 35, 30, 45, 55, 70, 60, 50, 40}
Komplexität der Versandhandelsabwicklung
Die zeitliche Komplexität der Postorder-Durchquerung beträgt An) , wobei 'n' die Größe des Binärbaums ist.
Die räumliche Komplexität der Postorder-Durchquerung hingegen beträgt O(1) , wenn wir die Stapelgröße für Funktionsaufrufe nicht berücksichtigen. Ansonsten beträgt die räumliche Komplexität der Postorder-Durchquerung Oh) , wobei „h“ die Höhe des Baumes ist.
Segmentierungsfehler-Kern gelöscht
Implementierung von Mail Order Traversal
Sehen wir uns nun die Implementierung der Postorder-Traversierung in verschiedenen Programmiersprachen an.
Programm: Schreiben Sie ein Programm zur Implementierung von Postorder-Traversal in der Sprache C.
#include #include struct node { s struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Ausgabe

Programm: Schreiben Sie ein Programm zur Implementierung von Postorder-Traversal in C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the postorder traversal of given binary tree is -
'; traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-14.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-15.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-16.webp" alt="Postorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Ausgabe
Nach der Ausführung des obigen Codes lautet die Ausgabe:

Programm: Schreiben Sie ein Programm zur Implementierung von Postorder-Traversal in Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } Ausgabe
Nach der Ausführung des obigen Codes lautet die Ausgabe:

Das ist also alles über den Artikel. Ich hoffe, der Artikel ist hilfreich und informativ für Sie.











