Regressions- und probabilistische Klassifizierungsprobleme können mithilfe des Gaußschen Prozesses (GP), einer überwachten Lerntechnik, gelöst werden. Da jeder Gaußsche Prozess als unendlichdimensionale Verallgemeinerung multivariater Prozesse betrachtet werden kann Gaußsche Verteilungen , der Begriff Gauß erscheint im Namen. Wir werden in diesem Beitrag Gaußsche Prozesse für die Regression besprechen, die auch als Gaußsche Prozessregression (GPR) bezeichnet werden. Zahlreiche reale Probleme in den Bereichen Materialwissenschaften, Chemie, Physik und Biologie wurden durch den Einsatz von GPR gelöst.
Inhaltsverzeichnis
- Gaußsche Prozessregression (GPR)
- Schlüsselkonzepte der Gaußschen Prozessregression (GPR)
- Mathematische Konzept der Gaußschen Prozessregression (GPR)
- Implementierung des Gaußschen Prozesses in Python
Gaußsche Prozessregression (GPR)
Die Gaußsche Prozessregression (GPR) ist eine leistungsstarke und flexible nichtparametrische Regressionstechnik, die in verwendet wird maschinelles Lernen Und Statistiken . Dies ist besonders nützlich, wenn es um Probleme mit kontinuierlichen Daten geht, bei denen die Beziehung zwischen Eingabevariablen und Ausgabe nicht explizit bekannt ist oder komplex sein kann. GPR ist ein Bayes'scher Ansatz, der die Sicherheit von Vorhersagen modellieren kann, was ihn zu einem wertvollen Werkzeug für verschiedene Anwendungen macht, einschließlich Optimierung, Zeitreihenvorhersage und mehr. GPR basiert auf dem Konzept eines Gaußschen Prozesses, bei dem es sich um eine Sammlung von Zufallsvariablen handelt, von denen jede endliche Anzahl eine gemeinsame Gaußsche Verteilung aufweist. Ein Gaußscher Prozess kann als eine Verteilung von Funktionen betrachtet werden.
Schlüsselkonzepte der Gaußschen Prozessregression (GPR)
Gaussain-Prozess
Ein nichtparametrisches, probabilistisches Modell namens a Gaußscher Prozess (GP) wird in der Statistik und beim maschinellen Lernen zur Regression, Klassifizierung und Unsicherheitsquantifizierung eingesetzt. Es stellt eine Gruppe von Zufallsvariablen dar, von denen jede eine gemeinsame Gaußverteilung aufweist und eine endliche Zahl haben kann. GPs sind eine vielseitige und effektive Technik zur Modellierung komplexer Zusammenhänge in Daten und zur Erstellung von Prognosen mit der damit verbundenen Unsicherheit.
Java-Programmierung umstellen
Eigenschaften von Gaußschen Prozessen :
- Nichtparametrische Natur : Allgemeinmediziner können sich an die Komplexität der Daten anpassen, da sie nicht auf eine festgelegte Anzahl von Modellparametern angewiesen sind
- Wahrscheinlichkeitsvorhersagen : Vorhersagen von Hausärzten können quantifiziert werden, da sie Vorhersagen als Wahrscheinlichkeitsverteilungen liefern.
- Interpolation und Glättung : GPs sind nützlich für verrauschte oder unregelmäßig abgetastete Daten, da sie verrauschte Daten gut glätten und zwischen Datenpunkten interpolieren können.
- Marginalisierung von Hyperparametern : Durch den Wegfall der Notwendigkeit einer expliziten Hyperparameter-Optimierung marginalisieren sie gegenüber Hyperparametern und machen das Modell einfacher.
Mittlere Funktion
Der vorhergesagte Wert der an jedem Eingabepunkt modellierten Funktion wird durch dargestellt mittlere Funktion in Gaußschen Prozessen (GPs). Es fungiert als grundlegende Annahme hinsichtlich der zugrunde liegenden Datenstruktur. Die Mittelwertfunktion ist häufig nicht unbedingt standardmäßig auf Null gesetzt und kann basierend auf Dateneigenschaften oder Domänenkenntnissen geändert werden. Durch die Beeinflussung der zentralen Tendenz von Prognosen hilft es Allgemeinmedizinern, Muster oder Trends in den Daten zu erkennen. GPs liefern probabilistische Vorhersagen, die sowohl Unsicherheiten als auch Punktschätzungen enthalten, indem sie die Mittelwertfunktion einbeziehen
Kovarianzfunktion (Kernel).
Der Kovarianzfunktion , auch als Kernelfunktion bezeichnet, misst, wie ähnlich die Eingabedatenpunkte in Gaußschen Prozessen (GPs) zueinander sind. Es ist wichtig für die Charakterisierung des Verhaltens des GP-Modells und beeinflusst die Auswahl von Funktionen aus der vorherigen Verteilung. Die Kovarianzfunktion misst paarweise Ähnlichkeiten, um die Korrelation zwischen Funktionswerten festzustellen. GPs können sich an ein breites Spektrum an Datenmustern anpassen, von glatten Trends bis hin zu komplexen Strukturen, da verschiedene Kernelfunktionen unterschiedliche Arten von Korrelationen erfassen. Die Leistung des Modells kann durch die Kernelauswahl stark beeinflusst werden.
Frühere Verteilungen
Der vorherige Verteilung , in Gaußschen Prozessen (GPs), ist unser Verständnis von Funktionen vor der Beobachtung von Daten. Normalerweise wird es durch eine Kovarianzfunktion (Kernelfunktion) und eine Mittelwertfunktion beschrieben. Während die Kovarianzfunktion die Ähnlichkeit oder Korrelation zwischen Funktionswerten an verschiedenen Eingabepunkten beschreibt, kodiert die Mittelwertfunktion unsere vorherigen Erwartungen. Dies wird vorab von Hausärzten genutzt, um eine Verteilung über Funktionen zu erstellen. Bei GPs können Priors ausgewählt werden, um Datenunsicherheit darzustellen, Domänenwissen zu integrieren oder Glätte anzuzeigen.
Hintere Verteilungen
Gaußsche Prozesse‘ spätere Verbreitung zeigt unsere überarbeiteten Annahmen über Funktionen nach Datenbeobachtung. Es setzt die Wahrscheinlichkeit der Daten angesichts der Funktion und der vorherigen Verteilung zusammen. Die Posterior-in-GP-Regression bietet eine Verteilung über Funktionen, die den beobachteten Daten am ehesten entsprechen. Indem sie probabilistische Vorhersagen und die Quantifizierung der Unsicherheit ermöglicht, spiegelt die Posterior-Verteilung den Kompromiss zwischen den in der Prior-Verteilung gespeicherten vorherigen Überzeugungen und den durch die Daten bereitgestellten Informationen wider.
Mathematische Konzept der Gaußschen Prozessregression (GPR)
Für Regressionsaufgaben wird ein nichtparametrisches, probabilistisches maschinelles Lernmodell namens Gaussian Process (GP)-Regression verwendet. Bei der Modellierung komplexer und mehrdeutiger Wechselwirkungen zwischen Eingabe- und Ausgabevariablen ist es ein leistungsstarkes Werkzeug. Es wird angenommen, dass eine multivariate Gaußsche Verteilung die Datenpunkte in der GP-Regression erzeugt, und das Ziel besteht darin, diese Verteilung abzuleiten.
Das GP-Regressionsmodell hat den folgenden mathematischen Ausdruck. Nehmen wir x an1, X2,…..,XNsind die Eingabedatenpunkte, wobei x zu reellen Zahlen (-2,-1,0,1…), (x) gehörtich
Nehmen wir an, y1, Und2,……., UndNsind die Ausgabewerte, wobei yichgehört zur reellen Zahl (yich
Das GP-Regressionsmodell geht davon aus, dass ein Gaußscher Prozess mit einer Mittelwertfunktion (
Dann ist die Verteilung von f an einer Reihe von Testorten x* wie folgt gegeben:
Typischerweise werden Kernelfunktionen verwendet, um die Mittelwertfunktion und die Kovarianzfunktion zu definieren. Zur Veranschaulichung wird der häufig verwendete quadratische Exponentialkern wie folgt beschrieben:
Wo,
k(x_{i}, x_{j}) = Die Kernelfunktion wird dadurch dargestellt und berechnet die Korrelation oder Ähnlichkeit zwischen zwei Eingabedatenpunkten xichund xJ.sigma^2 = Der Varianzparameter des Kernels ist dieser. Es legt die Skalierung oder vertikale Ausbreitung der Kernelfunktion fest. Es regelt, wie stark die Datenpunkte korrelieren. Ein höheressigma^2 ergibt eine Kernelfunktion mit größerer Varianz.- exp: Die Exponentialfunktion ist für die Potenz von e des Arguments verantwortlich.
||x_{i} – x_{j}||^2 : Die Differenz zwischen den Eingabedatenpunkten, xichund xJist der quadrierte euklidische Abstand. Der geometrische Abstand zwischen den Punkten im Merkmalsraum wird gemessen.- l2: Dies ist eine Darstellung der Längenskala oder charakteristischen Länge des Kernels. Es reguliert die Geschwindigkeit, mit der sich die Kernelfunktion verschlechtert, wenn die Datenpunkte weiter voneinander entfernt sind. Ein niedrigeres l führt zu einer schnelleren Verschlechterung des Kernels.
Das GP-Regressionsmodell wendet die Bayes'sche Inferenz an, um die Verteilung von f zu bestimmen, die bei einem gegebenen Satz von Trainingsdaten (x, y) am wahrscheinlichsten die Daten erzeugt hat. Dazu muss die Posteriorverteilung von f anhand der Daten berechnet werden, die wie folgt definiert ist:
Dabei ist die Grenzwahrscheinlichkeit der Daten p(y|x), die A-priori-Verteilung von f ist p(f) und die Wahrscheinlichkeit der Daten bei gegebener Funktion f ist (y|x,f).
Nachdem das Modell die hintere Verteilung von f gelernt hat, berechnet es die hintere Vorhersageverteilung, um Vorhersagen für zusätzliche Testpunkte x* zu treffen. Es kann wie folgt definiert werden:
Wo,
p(f^*|x*, y, x) = Dies zeigt bei gegebenen Trainingsdaten y und x die bedingte Wahrscheinlichkeit der vorhergesagten Funktionswerte f*an einem neuen Eingabepunkt x*Anders ausgedrückt handelt es sich um die Wahrscheinlichkeitsverteilung über alle potenziellen Funktionswerte am neuen Eingabeort x*, abhängig von den beobachteten Daten y und ihren passenden Eingabeorten x.int p(f^*|x^*, f)p(f|y,x)df = In diesem Abschnitt der Gleichung wird ein Integral verwendet, um die bedingte Wahrscheinlichkeit zu bestimmen. Das Integral umfasst alle möglichen Werte der Funktion f.p(f^*|x^*, f) = Dies ist die bedingte Wahrscheinlichkeitsverteilung der erwarteten Funktionswerte f*bei x*, gegeben die Funktionswerte f an einigen Zwischenstellen.p(f|y,x) = Angesichts der beobachteten Daten (y) und ihrer Eingabeorte (x) ist dies die bedingte Wahrscheinlichkeitsverteilung der Funktionswerte (f).
Für Aufgaben wie unsichere Entscheidungsfindung und aktives Lernen bietet diese Verteilung ein Maß für die Unsicherheit der Vorhersage, was hilfreich sein kann.
Schritte in der Gaußschen Prozessregression
- Datensammlung : Sammeln Sie die Eingabe-Ausgabe-Datenpaare für Ihr Regressionsproblem.
- Wählen Sie eine Kernel-Funktion : Wählen Sie eine geeignete Kovarianzfunktion (Kernel), die zu Ihrem Problem passt. Die Wahl des Kernels beeinflusst die Form der Funktionen, die GPR modellieren kann.
- Parameteroptimierung : Schätzen Sie die Hyperparameter der Kernelfunktion, indem Sie die Wahrscheinlichkeit der Daten maximieren. Dies kann mithilfe von Optimierungstechniken wie dem Gradientenabstieg erfolgen.
- Vorhersage: Verwenden Sie bei einer neuen Eingabe das trainierte GPR-Modell, um Vorhersagen zu treffen. GPR liefert sowohl den vorhergesagten Mittelwert als auch die damit verbundene Unsicherheit (Varianz).
Implementierung der Gaußschen Prozessregression (GPR)
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Ausgabe:
Ersatz in Java
Generieren Sie in diesem Code zunächst einige Beispieldatenpunkte mit zusätzlichem Rauschen, definieren Sie dann einen RBF-Kernel und erstellen Sie einen Gaußscher Prozessregressor damit. Das Modell wird anhand der Trainingsdaten trainiert und verwendet, um Vorhersagen anhand der Testdaten zu treffen. Abschließend werden die Ergebnisse mit einem Diagramm visualisiert, das die Trainingsdaten, den vorhergesagten Mittelwert und das 95 %-Konfidenzintervall zeigt.
Implementierung des Gaußschen Prozesses in Python
Scikit Learn
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Die notwendigen Bibliotheken für die Gaußsche Prozessregression (GPR) in Python werden durch diesen Code importiert; diese sind SciPy für lineare Algebrafunktionen, NumPy für numerische Operationen und Matplotlib zur Datenvisualisierung. Um sicherzustellen, dass es mit den erforderlichen Paketen kompatibel ist, überprüft es zusätzlich die Version von Python und druckt sie zusammen mit den Versionen von NumPy und scikit-learn (sklearn).
Kernel-Auswahl
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Ausgabe:
[RBF(length_scale=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(length_scale=1, periodicity=10),
DotProduct(sigma_0=1) ** 2,
Mütterlich(length_scale=1, nu=1.5)]
Der Code gibt die Anzahl der Teststandorte (n) an und initialisiert a zufälliger Samen . Um die ausgewählten Kernel anzuzeigen, generiert es eine Liste mehrerer Kernelfunktionen und druckt die Liste aus.
Kernel-Vergleich und Visualisierung
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Ausgabe:
RBF
gp.kernel_ RBF(length_scale=1.93)
gp.log_marginal_likelihood: -3.444937833462133
-------------------------------------------------- -
Rational Quadratisch

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1.93)
gp.log_marginal_likelihood: -3.4449718909150966
--------------------------------------------------
ExpSineSquared

gp.kernel_ ExpSineSquared(length_scale=0.000524, periodicity=2.31e+04)
gp.log_marginal_likelihood: -3.4449381454930217
--------------------------------------------------
Skalarprodukt

gp.kernel_ DotProduct(sigma_0=0.998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------
Mütterlich

gp.kernel_Matern(length_scale=1.99, nu=1.5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------
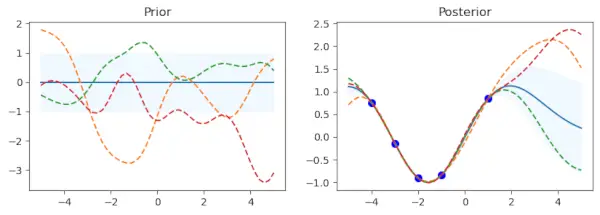
Der Code beginnt mit einer Schleife über die verschiedenen Kernelfunktionen, die in der Liste „kernel_“ aufgeführt sind. Für jeden Kernel wird unter Verwendung des jeweiligen Kernels ein Gaußscher Prozessregressor (gp) erstellt. Für den Gaußschen Prozess wird dadurch die Kovarianzstruktur festgelegt. Um die vorherige Verteilung zu bewerten, wird ein Satz von Testeingabepunkten namens x_test mit Werten im Bereich von -5 bis 5 erstellt. Dieser Satz von Punkten wird in einen Spaltenvektor umgewandelt.
Mithilfe der gp.predict-Methode werden der Mittelwert (mu_prior) und die Standardabweichung (sd_prior) der vorherigen Verteilung an jedem Testpunkt bestimmt. Standardabweichungswerte werden mit der Option return_std=True angefordert. gp.sample_y (x_test, 3) wird verwendet, um drei Funktionsbeispiele aus der vorherigen Verteilung abzurufen.
Das erste Unterdiagramm zeigt den Mittelwert der vorherigen Verteilung, wobei die Standardabweichung durch einen schattierten Bereich dargestellt wird. Die Stichproben werden als gestrichelte Linien überlagert, während der Mittelwert als durchgezogene Linie dargestellt wird. Es gibt eine Nebenhandlung namens Prior. Es gibt einen definierten Satz von Trainingsdatenpunkten (x_train) und dazugehörigen Zielwerten (y_train). Das Gaußsche Prozessmodell wird mithilfe dieser Punkte angepasst (gp.fit(x_train, y_train)). Fünf Datenpunkte mit entsprechenden Sinuswerten bilden die Trainingsdaten in diesem Code.
CSS-Grenze
Nach der Anpassungsphase der Trainingsdaten berechnet das Verfahren den Mittelwert (mu_post) und die Standardabweichung (sd_post) der Posteriorverteilung für dieselben Testpunkte (x_test). gp.sample_y(x_test, 3) wird auch verwendet, um Funktionsstichproben aus der Posterior-Verteilung zu erzeugen. Das zweite Unterdiagramm überlagert die Stichprobenfunktionen als gepunktete Linien und zeigt den Mittelwert der Posterior-Verteilung, schattiert mit der Standardabweichung. Blau dargestellt sind die Trainingsdatenpunkte. Die Nebenhandlung trägt den Namen Posterior.
Um die vorherigen und hinteren Diagramme für den aktuellen Kernel anzuzeigen und ein visuelles Verständnis des Verhaltens des Modells zu erhalten, rufen Sie die Funktion plt.show() von Matplotlib auf.
Der Code zeigt Details zum aktuellen Kernel an, z. B. gp.kernel_, der den aktuell verwendeten Kernel angibt, und gp.log_marginal_likelihood (gp.kernel_.theta), das die logarithmische Grenzwahrscheinlichkeit des Modells angibt, das den aktuellen Kernel verwendet, nach jedem Satz von vorherigen und hinteren Diagrammen.
Vorteile der Gaußschen Prozessregression (GPR)
Die Gaußsche Prozessregression (GPR) bietet in einer Reihe von Anwendungen eine Reihe von Vorteilen:
- GPR bietet einen probabilistischen Rahmen für die Regression, was bedeutet, dass es nicht nur Punktschätzungen, sondern auch Unsicherheitsschätzungen für Vorhersagen liefert.
- Es ist hochflexibel und kann komplexe Zusammenhänge in den Daten erfassen.
- GPR kann an verschiedene Anwendungen angepasst werden, einschließlich Zeitreihenvorhersage, Optimierung und Bayes'sche Optimierung.
Herausforderungen der Gaußschen Prozessregression (GPR)
- GPR kann beim Umgang mit großen Datensätzen rechenintensiv sein, da die Invertierung einer Kovarianzmatrix erforderlich ist.
- Die Wahl der Kernelfunktion und ihrer Hyperparameter kann die Leistung des Modells erheblich beeinflussen.
Gute Beispiele für GPR-Anwendungen
- Aktienkursprognose: GPR kann zur Modellierung und Vorhersage von Aktienkursen unter Berücksichtigung der Volatilität und Unsicherheit auf den Finanzmärkten verwendet werden.
- Computerexperimente: GPR eignet sich zur Optimierung komplexer Simulationen, indem es die Input-Output-Beziehungen modelliert und die einflussreichsten Parameter identifiziert.
- Anomalieerkennung: GPR kann zur Anomalieerkennung eingesetzt werden, wo ungewöhnliche Muster in Zeitreihendaten durch die Erfassung normaler Datenverteilungen identifiziert werden.
Abschluss
Zusammenfassend lässt sich sagen, dass die Gaußsche Prozessregression ein wertvolles Werkzeug für die Datenanalyse und Vorhersage in Situationen ist, in denen es wichtig ist, die Unsicherheit in Vorhersagen zu verstehen. Durch die Nutzung probabilistischer Modellierung und Kernelfunktionen kann GPR genaue und interpretierbare Ergebnisse liefern. Bei der praktischen Umsetzung von GPR ist es jedoch wichtig, den Rechenaufwand und den Bedarf an Expertenbeiträgen zu berücksichtigen.
