Die Höhe oder Tiefe eines Binärbaums kann als die maximale oder größte Anzahl von Kanten von einem Blattknoten zum Wurzelknoten oder vom Wurzelknoten zum Blattknoten definiert werden. Der Wurzelknoten befindet sich auf der Ebene Null. Das heißt, wenn mit dem Wurzelknoten keiner der untergeordneten Knoten verbunden ist, wird die Höhe oder Tiefe des jeweiligen Binärbaums als Null bezeichnet.
Nehmen wir ein Beispiel, um die Höhe des Binärbaums besser zu verstehen.
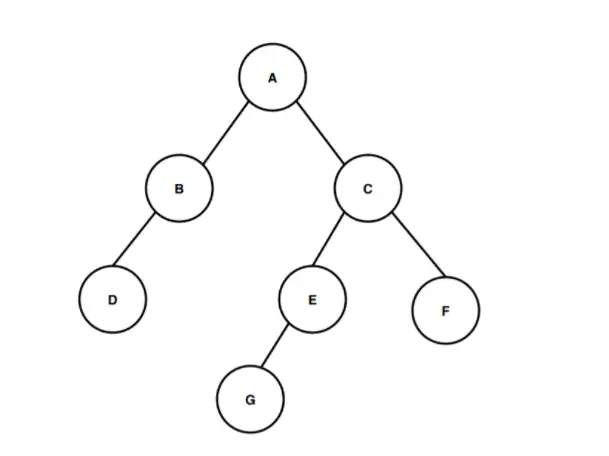
Im obigen Bild haben wir einen Binärbaum, der beim Wurzelknoten A beginnt. Der Wurzelknoten A hat zwei untergeordnete Knoten B und C als linkes bzw. rechtes untergeordnetes Kind. Und in ähnlicher Weise hat der linke untergeordnete Knoten B nur einen linken untergeordneten Knoten namens D, und der rechte untergeordnete Knoten C hat zwei untergeordnete Knoten E und F, von denen Knoten E den Knoten G als einzigen linken untergeordneten Knoten hat.
Powershell kleiner oder gleich
Berechnen wir nun die Höhe dieses Binärbaums. Zählen Sie die Anzahl der Kanten vom Wurzelknoten bis zum tiefsten Blattknoten, um die Höhe des Binärbaums zu berechnen. Der tiefste Knoten, der in diesem Binärbaum vorhanden ist, ist der Knoten G. Zur Berechnung der Höhe oder Tiefe dieses Binärbaums müssen wir also die Anzahl der Kanten zwischen dem Wurzelknoten und dem tiefsten Knoten G berechnen. Die erste Kante verläuft vom Knoten A zum Knoten C, die zweite Kante verläuft vom Knoten C zum Knoten E und die dritte Kante verläuft vom Knoten E zum Knoten G. Für den Übergang vom Wurzelknoten A zum tiefsten Knoten G gibt es also drei Kanten , also beträgt die Höhe oder Tiefe des Binärbaums 3. Der Pfad, dem wir gefolgt sind, um von der Wurzel zum tiefsten Blattknoten zu gelangen, ist A > C > E > G und dieser Pfad deckt während der Durchquerung drei Kanten ab, deshalb gemäß Zur Definition der Höhe des Binärbaums beträgt die Höhe dieses Binärbaums 3.
Möglichkeiten, die Höhe des Binärbaums zu ermitteln
Schreiben wir nun Code, um die Höhe eines Binärbaums zu ermitteln. Es gibt zwei Möglichkeiten, die Höhe des Binärbaums zu ermitteln. Einer ist der rekursive Methode und das andere ist das nicht rekursive Methode Dabei wird die Warteschlangendatenstruktur verwendet, um die Höhe des Binärbaums zu berechnen.
Rekursiver Weg
Sehen wir uns zunächst die rekursive Methode zum Ermitteln der Höhe des Binärbaums an.
Code:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Ausgabe: Die Ausgabe des obigen Codes ist:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
Auf rekursive Weise haben wir das aufgerufen Höhe() Führen Sie die Funktion wiederholt aus, um die Höhe des Binärbaums zu ermitteln. Der Wurzelknoten des Binärbaums wird als Parameter an die Funktion height() übergeben. Die Funktion height() berechnet die Höhe beider Teilbäume des Wurzelknotens und welche der beiden Höhen höher ist, wird als Höhe des Binärbaums betrachtet.
Nicht rekursiver Weg
Sehen wir uns nun die nichtrekursive Methode zum Ermitteln der Höhe des Binärbaums an.
Shreya Ghoshal erster Ehemann
Code:
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> Bei diesem Ansatz haben wir eine nicht rekursive Methode verwendet, um die Tiefe des Binärbaums zu ermitteln. Um die Höhe des Binärbaums zu ermitteln, haben wir eine Funktion namens height geschrieben, die einen Parameter vom Typ „Knoten“ erfordert (d. h. die Wurzel des Binärbaums, dessen Höhe berechnet werden muss). Die Wurzel des Binärbaums befindet sich auf der Ebene Null, was bedeutet, dass die Höhe oder Tiefe der Wurzel Null ist.
Beim nicht rekursiven Ansatz verwenden wir die Warteschlangendatenstruktur, um die Tiefe des Binärbaums zu ermitteln. Die Knoten des Binärbaums, für die wir die Tiefe ermitteln möchten, werden mit Hilfe einer Enqueue-Operation zur Queue-Datenstruktur hinzugefügt, wobei der Knoten des Binärbaums als Parameter an diese Funktion übergeben wird.
Sobald alle Knoten zur Warteschlange hinzugefügt wurden, werden die zur Warteschlange hinzugefügten Knoten durch Aufrufen der Dequeue-Funktion entfernt, die so lange ein Element aus der Warteschlange entfernt, bis der Nullknoten des Binärbaums gefunden wird. Jedes Mal, wenn ein Knoten des Binärbaums aus der Warteschlange entfernt wird, wird die Tiefenvariable, die die Tiefe des Binärbaums darstellt, um eins erhöht. Und am Ende repräsentiert der Wert der Tiefenvariablen die endgültige Tiefe des Binärbaums.
