Der Winkel wird in Grad (°) und Bogenmaß gemessen. Es wird zwischen den beiden benachbarten Seiten eines Polygons gebildet. Jedes Polygon hat unterschiedliche Seiten und eine unterschiedliche Anzahl von Winkeln. Die Formel zum Ermitteln der Winkel in Grad ist in der Geometrie und Trigonometrie nützlich. Es ist wichtig, andere Konzepte der Mathematik zu verstehen, wie zum Beispiel den Bogen, den Mittelpunktswinkel des Kreises usw.

1. Ein Vollkreis = 360°
2. Eine Gerade = 180°
3. Ein Halbkreis = 180°
4. Ein Viertelkreis = 90°

Winkel in Grad berechnen

Es gibt drei verschiedene Methoden zum Ermitteln von Winkeln in Grad:

1. Verwendung des Protektors D
2. Mithilfe des Satzes des Pythagoras und der Trigonometriefunktion wird ein rechtwinkliges Dreieck erstellt
3. Verwendung der Winkelsummenformel
4. Zentralwinkel eines Kreises

Verwendung des Protektors D

Ein Protektor ist eine Art Lineal oder Maßstab, mit dem Entfernungen in Zentimetern oder Millimetern gemessen werden. Der zum Messen von Winkeln verwendete Schutz hat die Form eines „D“, wobei der Winkelwert von 0 bis 180 ° aus jeder Richtung (rechts oder links) markiert ist. Wir müssen die Achse an der Linie auf dem D ausrichten, um den Winkel zu messen. Der mittlere Kreis des Protektors ist auf den Scheitelpunkt des zu messenden Winkels ausgerichtet. Die Strahlen entlang des Scheitelpunkts des Winkels helfen dabei, den Winkel in Grad zu ermitteln.

Verwendung des Satzes des Pythagoras und der Trigonometriefunktion in einem rechtwinkligen Dreieck

In der Trigonometrie gibt es sechs Funktionen: Sinus, Cos, Cosec, Tan, Kinderbett, Und Sek. Ein rechtwinkliges Dreieck hat drei Seiten: Basis, Senkrechte und Hypotenuse.

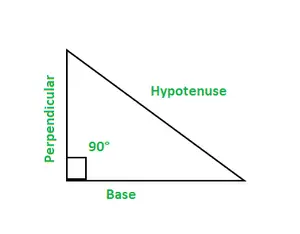
Basis: Es ist eine angrenzende Seite zum Winkel von 90°. Senkrecht: Es ist auch eine angrenzende Seite zum Winkel von 90°. Hypotenuse: Es ist eine Seite, die dem Winkel von 90° gegenüberliegt.

Ein rechtwinkliges Dreieck wird durch einen Winkel von 90° als einen der Winkel dargestellt. Die Gesamtwinkelsumme eines Dreiecks beträgt 180°.

Cosecθ: Wird als Hypotenuse dividiert durch die Senkrechte dargestellt.

Cosecθ =

Cotθ: Es wird als Basis dividiert durch die Senkrechte dargestellt.

Cotθ =

Die anderen trigonometrischen Funktionen werden dargestellt als:

sinθ =

Cosθ =

tanθ =

Sekθ =

Cosecθ kann auch als 1/ sinθ dargestellt werden

secθ kann auch als 1/cosθ dargestellt werden

Cotθ kann auch als 1/tanθ dargestellt werden

Wo,

Θ ist der Winkel

Satz des Pythagoras

Wenn zwei Seiten eines rechten Winkels bekannt sind, können wir die dritte Seite eines rechtwinkligen Dreiecks leicht berechnen. In einem rechtwinkligen Dreieck ist der Satz des Pythagoras gegeben durch:

(Hypotenuse)²= (Basis)²+ (senkrecht)²

Formel für die Winkelsumme

Die Winkelsumme bezieht sich auf die Gesamtsumme der Innenwinkel eines Polygons, die sich zwischen den beiden Seiten bilden. Wenn ein Polygon sechs Seiten hat, gibt es etwa sechs Winkel. Es hilft, einen Winkel zu finden, wenn andere Winkel und die Winkelsumme eines Polygons bekannt sind.

Die Formel zum Ermitteln der Gesamtwinkelsumme eines Polygons lautet:

Gesamtwinkelsumme = 180 (n – 2)

Wo,

n ist die Anzahl der Seiten eines Polygons

Beispiel:

• Wenn n = 4,

Gesamtwinkelsumme = 180 (4 – 2)

= 180 (2)

= 360°

Wenn n = 5,

Gesamtwinkelsumme = 180 (5 – 2)

= 180 (3)

= 540°

• Wenn n = 6

Gesamtsumme der Winkel = 180 (6 – 2)

= 180 (4)

= 720°

Zentralwinkel eines Kreises

Ein Kreis ist eine runde Figur, deren Rand den gleichen Abstand von ihrem Mittelpunkt hat. Der Abstand zwischen dem Mittelpunkt und der Grenze wird als Kreisradius bezeichnet. Der Winkel, den die beiden Radien des Kreises bilden, wird Mittelpunktswinkel genannt. Der Mittelpunktswinkel eines Kreises liegt zwischen 0 und 360 Grad.

Die Formel zur Berechnung des Mittelpunktswinkels eines Kreises lautet:

Bogenlänge = 2πr × (θ/360)

Θ = 360L/2pr

Wo,

r ist der Radius des Kreises

AB ist der Bogen

Theta ist der Winkel in Grad.

L = Bogenlänge

Beispielprobleme

Frage 1: Finden Sie den Mittelpunktswinkel eines Kreises mit einem Radius von 2 m und einer Bogenlänge von 4 m?

Lösung :

Die Formel zur Berechnung des Mittelpunktswinkels eines Kreises lautet:

Θ = 360L/2pr

Wo,

r ist der Radius des Kreises

Theta ist der Winkel in Grad.

L = Bogenlänge

Θ = Winkel in Grad

Zeichenfolge vergleichen mit

r = 2m

L = 4m

Θ = 360 × 4 /2 × π × 2

Θ = 114,6°

Somit beträgt der Mittelpunktswinkel des Kreises 114,6°.

Frage 2: Finden Sie den Mittelpunktswinkel eines Kreises mit einem Radius von 10 cm und einer Bogenlänge von 18 cm?

Lösung :

Die Formel zur Berechnung des Mittelpunktswinkels eines Kreises lautet:

Θ = 360L/2pr

Wo,

r ist der Radius des Kreises

Theta ist der Winkel in Grad.

L = Bogenlänge

r = 10cm

L = 18 cm

Θ = Winkel in Grad

Θ = 360 × 18 /2 × π × 10

Θ = 103,13°

Somit beträgt der Mittelpunktswinkel des Kreises 103,13°.

Frage 3: Finden Sie den Winkel eines Parallelogramms, wenn die anderen drei Winkel 80°, 95° und 105° betragen?

Lösung :

Es gibt vier Seiten in einem Parallelogramm mit einer Gesamtwinkelsumme von 360°.

Formel zur Ermittlung der Winkelsumme = 180 (n – 2)

Wo,

n ist die Anzahl der Seiten eines Polygons

Hier ist n = 4,

Die Gesamtsumme der Winkel = 180 (4 – 2)

= 180 (2)

= 360°

Gesamtsumme = Winkel 1 + Winkel 2 + Winkel 3 + Winkel 4

360 = 80+ 95+ 105+ Winkel 4

360 = 280 + Winkel 4

Winkel 4 = 360 – 280

Winkel 4 = 80°

Frage 4: Finden Sie den Winkel A in der angegebenen Abbildung.

Lösung :

Gegeben: Hypotenuse = 12

Senkrecht = 6

Die Trigonometriefunktion zur Berechnung des Winkels ist gegeben durch:

sinA = 6/12

A = 30°

Frage 5: Finden Sie den Winkel A in der angegebenen Abbildung.

Lösung :

Gegeben: Hypotenuse = 10

Basis= 5

Die Trigonometriefunktion zur Berechnung des Winkels ist gegeben durch:

CosA = 5/10

A = 60°

Frage 6: Finden Sie den Winkel eines Fünfecks, wenn die anderen vier Winkel 115°, 100°, 105° und 100° sind?

Lösung :

Es gibt fünf Seiten in einem Fünfeck mit einer Gesamtwinkelsumme von 540°.

Formel zur Ermittlung der Winkelsumme = 180 (n – 2)

Wo,

n ist die Anzahl der Seiten eines Polygons

Hier ist n = 5,

Gesamtwinkelsumme = 180 (5 – 2)

= 180 (3)

= 540°

Gesamtsumme = Winkel 1 + Winkel 2 + Winkel 3 + Winkel 4 + Winkel 5

540 = 115° + 100° + 105°+100° + Winkel 5

540 = 420 + Winkel 5

Winkel 5 = 540 – 420

Winkel 5 = 120°

Frage 7: Finden Sie den Winkel A in der angegebenen Abbildung.

Lösung :

Gegeben: Basis = √3

Senkrecht= 1

Die Trigonometriefunktion zur Berechnung des Winkels ist gegeben durch:

tanθ =

tanθ = 1/√3

A = 30°

Frage 8: Finden Sie den Winkel eines Parallelogramms, wenn die anderen drei Winkel 100°, 70° und 80° sind?

Lösung :

Es gibt vier Seiten in einem Parallelogramm mit einer Gesamtwinkelsumme von 360°.

Formel zur Ermittlung der Winkelsumme = 180 (n – 2)

Wo,

n ist die Anzahl der Seiten eines Polygons

Hier ist n = 4,

Gesamtsumme der Winkel = 180 (4 – 2)

= 180 (2)

= 360°

Gesamtsumme = Winkel 1 + Winkel 2 + Winkel 3 + Winkel 4

360 = 100 + 70 + 80 + Winkel 4

360 = 250 + Winkel 4

Winkel 4 = 360 – 250

Winkel 4 = 110°

Somit beträgt der andere Winkel 110°.

Frage 9: Finden Sie den Winkel eines Sechsecks, wenn die anderen fünf Winkel 120°, 115°, 110°, 125° und 105° sind?

Lösung :

Ein Sechseck hat sechs Seiten mit einer Gesamtwinkelsumme von 720°.

Formel zur Ermittlung der Winkelsumme = 180 (6 – 2)

Wo,

n ist die Anzahl der Seiten eines Polygons

Hier ist n = 6,

Gesamtsumme der Winkel = 180 (6 – 2)

= 180 (4)

= 720°

Gesamtsumme = Winkel 1 + Winkel 2 + Winkel 3 + Winkel 4 + Winkel 5 + Winkel 6

720 = 120 + 115 + 110 + 125 + 105 + Winkel 6

720 = 575 + Winkel 6

Winkel 6 = 720 – 575

Winkel 6 = 145°

Somit beträgt der sechste Winkel des Sechsecks 145°.