AVL-Baum:
Der AVL-Baum ist ein selbstausgleichender binärer Suchbaum ( BST ), wobei der Unterschied zwischen den Höhen des linken und rechten Teilbaums nicht mehr als betragen darf eins für alle Knoten.
Beispiel eines AVL-Baums:
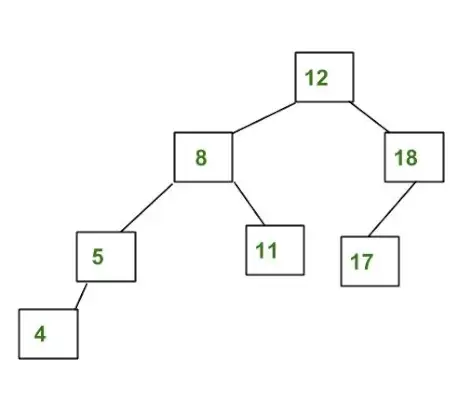
Der obige Baum ist AVL, da die Unterschiede zwischen den Höhen der linken und rechten Teilbäume für jeden Knoten kleiner oder gleich 1 sind.
Beispiel eines Baums, der KEIN AVL-Baum ist:

Der obige Baum ist kein AVL, da die Unterschiede zwischen den Höhen des linken und rechten Teilbaums für 8 und 12 größer als 1 sind.
Warum AVL-Bäume?
Die meisten BST-Operationen (z. B. Suchen, Max, Min, Einfügen, Löschen usw.) dauern Oh) Zeit wo H ist die Höhe des BST. Die Kosten für diese Operationen können steigen An) Für ein verzerrter Binärbaum . Wenn wir darauf achten, dass die Höhe des Baumes erhalten bleibt O(log(n)) Nach jedem Einfügen und Löschen können wir eine Obergrenze von garantieren O(log(n)) für alle diese Operationen. Die Höhe eines AVL-Baums beträgt immer O(log(n)) Wo N ist die Anzahl der Knoten im Baum.
Einfügen im AVL-Baum:
Um sicherzustellen, dass der gegebene Baum nach jeder Einfügung AVL bleibt, müssen wir die standardmäßige BST-Einfügungsoperation erweitern, um einen gewissen Neuausgleich durchzuführen.
Im Folgenden sind zwei grundlegende Operationen aufgeführt, die ausgeführt werden können, um einen BST auszugleichen, ohne die BST-Eigenschaft zu verletzen (keys(left)
- Linksdrehung
- Rechtsdrehung
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x / Right Rotation / x T3 - - - - - - ->T1 und / <- - - - - - - / T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>Empfohlene Praxis zum Einfügen von AVL-Bäumen Probieren Sie es aus!
Schritte zum Einfügen:
Sei der neu eingefügte Knoten In
- Standard ausführen BST einfügen für In .
- Ab In , reise nach oben und finde den ersten unausgeglichener Knoten . Lassen Mit der erste unausgeglichene Knoten sein, Und sei der Kind von Mit Das kommt auf dem Weg von In Zu Mit Und X sei der Enkel von Mit Das kommt auf dem Weg von In Zu Mit .
- Bringen Sie den Baum wieder ins Gleichgewicht, indem Sie entsprechende Drehungen am Teilbaum durchführen, der mit verwurzelt ist Mit. Es kann 4 mögliche Fälle geben, die behandelt werden müssen x,y Und Mit kann auf 4 Arten angeordnet werden.
- Im Folgenden sind die vier möglichen Anordnungen aufgeführt:
- y ist das linke Kind von z und x ist das linke Kind von y (Links-Links-Fall)
- y ist das linke Kind von z und x ist das rechte Kind von y (Links-Rechts-Fall)
- y ist das rechte Kind von z und x ist das rechte Kind von y (Rechts-Rechts-Fall)
- y ist das rechte Kind von z und x ist das linke Kind von y (Rechts-Links-Fall)
Im Folgenden sind die Vorgänge aufgeführt, die in den oben genannten 4 Fällen durchgeführt werden müssen. In allen Fällen müssen wir nur wieder ins Gleichgewicht bringen Der Teilbaum hat seine Wurzeln Mit und der gesamte Baum wird ausgeglichen, wenn die Höhe des Teilbaums (nach entsprechenden Rotationen) mit verwurzelt ist Mit wird derselbe wie vor dem Einfügen.
1. Linker linker Fall
T1, T2, T3 and T4 are subtrees. z y / / y T4 Right Rotate (z) x z / - - - - - - - - ->/ / x T3 T1 T2 T3 T4 / T1 T2>
2. Links-Rechts-Gehäuse
z z x / / / y T4 Left Rotate (y) x T4 Right Rotate(z) y z / - - - - - - - - ->/ - - - - - - - -> / / T1 x y T3 T1 T2 T3 T4 / / T2 T3 T1 T2>
3. Richtiger richtiger Fall
z y / / T1 y Left Rotate(z) z x / - - - - - - - ->/ / T2 x T1 T2 T3 T4 / T3 T4>
4. Rechts-Links-Fall
z z x / / / T1 y Right Rotate (y) T1 x Left Rotate(z) z y / - - - - - - - - ->/ - - - - - - - -> / / x T4 T2 y T1 T2 T3 T4 / / T2 T3 T3 T4>
Abbildung der Einfügung im AVL-Baum





Ansatz:
Die Idee besteht darin, die rekursive BST-Einfügung zu verwenden. Nach der Einfügung erhalten wir einen Zeiger auf alle Vorfahren, einen nach dem anderen, von unten nach oben. Wir brauchen also keinen übergeordneten Zeiger, um nach oben zu reisen. Der rekursive Code selbst wandert nach oben und besucht alle Vorfahren des neu eingefügten Knotens.
Befolgen Sie die unten aufgeführten Schritte, um die Idee umzusetzen:
- Führen Sie das Normale aus BST-Insertion.
- Der aktuelle Knoten muss einer der Vorgänger des neu eingefügten Knotens sein. Aktualisieren Sie die Höhe des aktuellen Knotens.
- Ermitteln Sie den Gleichgewichtsfaktor (Höhe des linken Teilbaums – Höhe des rechten Teilbaums) des aktuellen Knotens.
- Wenn der Ausgleichsfaktor größer ist als 1, dann ist der aktuelle Knoten unausgeglichen und wir befinden uns entweder im Linker Linker Fall oder links Rechts Fall . Um zu überprüfen, ob es so ist linker linker Fall oder nicht, vergleichen Sie den neu eingefügten Schlüssel mit dem Schlüssel im linke Teilbaumwurzel .
- Wenn der Ausgleichsfaktor kleiner ist als -1 , dann ist der aktuelle Knoten unausgeglichen und wir befinden uns entweder im Rechts-Rechts-Fall oder im Rechts-Links-Fall. Um zu überprüfen, ob es sich um den Right Right-Fall handelt oder nicht, vergleichen Sie den neu eingefügten Schlüssel mit dem Schlüssel in der rechten Teilbaumwurzel.
Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:
C++14
// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->Höhe;> }> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>B)? a : b;> }> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->Schlüssel = Schlüssel;> >node->links = NULL;> >node->rechts = NULL;> >node->Höhe = 1;>// new node is initially> >// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->links;> >Node *T2 = x->Rechts;> > >// Perform rotation> >x->rechts = y;> >y->links = T2;> > >// Update heights> >y->height = max(height(y->left),> >height(y->rechts)) + 1;> >x->height = max(height(x->left),> >height(x->rechts)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->Rechts;> >Node *T2 = y->links;> > >// Perform rotation> >y->links = x;> >x->rechts = T2;> > >// Update heights> >x->height = max(height(x->left),> >height(x->rechts)) + 1;> >y->height = max(height(y->left),> >height(y->rechts)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->links) - Höhe(N->rechts);> }> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->left = insert(node->left, key);> >else> if> (key>Knoten->Schlüssel)> >node->right = insert(node->right, key);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->height = 1 + max(height(node->left),> >height(node->Rechts));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 &&-Taste links->Taste)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->Rechts->Taste)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && key> node->left->key)> >{> >node->left = leftRotate(node->left);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->Schlüssel)> >{> >node->right = rightRotate(node->right);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >cout ' '; preOrder(root->links); Vorbestellung(root->right); } } // Treibercode int main() { Node *root = NULL; /* Konstruieren des in der obigen Abbildung angegebenen Baums */ root = insert(root, 10); root = insert(root, 20); root = insert(root, 30); root = insert(root, 40); root = insert(root, 50); root = insert(root, 25); /* Der konstruierte AVL-Baum wäre 30 / 20 40 / 10 25 50 */ cout<< 'Preorder traversal of the ' 'constructed AVL tree is
'; preOrder(root); return 0; } // This code is contributed by // rathbhupendra> |
>
>
C
// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->Höhe;> }> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>B)? a : b;> }> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->Schlüssel = Schlüssel;> >node->links = NULL;> >node->rechts = NULL;> >node->Höhe = 1;>// new node is initially added at leaf> >return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->links;> >struct> Node *T2 = x->Rechts;> > >// Perform rotation> >x->rechts = y;> >y->links = T2;> > >// Update heights> >y->height = max(height(y->left),> >height(y->rechts)) + 1;> >x->height = max(height(x->left),> >height(x->rechts)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->Rechts;> >struct> Node *T2 = y->links;> > >// Perform rotation> >y->links = x;> >x->rechts = T2;> > >// Update heights> >x->height = max(height(x->left),> >height(x->rechts)) + 1;> >y->height = max(height(y->left),> >height(y->rechts)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->links) - Höhe(N->rechts);> }> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->left = insert(node->left, key);> >else> if> (key>Knoten->Schlüssel)> >node->right = insert(node->right, key);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->height = 1 + max(height(node->left),> >height(node->Rechts));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 &&-Taste links->Taste)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->Rechts->Taste)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && key> node->left->key)> >{> >node->left = leftRotate(node->left);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->Schlüssel)> >{> >node->right = rightRotate(node->right);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->Schlüssel);> >preOrder(root->links);> >preOrder(root->Rechts);> >}> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >' tree is
'>);> >preOrder(root);> > >return> 0;> }> |
>
>
Java
// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>B) ? a : b;> >}> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); else // Doppelte Schlüssel nicht zulässig return node; /* 2. Höhe dieses Vorgängerknotens aktualisieren */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Holen Sie sich den Gleichgewichtsfaktor dieses Vorgängerknotens, um zu prüfen, ob dieser Knoten unausgeglichen ist */ int balance = getBalance(node); // Wenn dieser Knoten unausgeglichen wird, gibt es // 4 Fälle Left Left Case if (balance> 1 && key return rightRotate(node); // Right Right Case if (balance<-1 && key>node.right.key) return leftRotate(node); // Left Right Case if (balance> 1 && key> node.left.key) { node.left = leftRotate(node.left); return rightRotate(node); } // Rechts-Links-Fall if (balance<-1 && key node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { System.out.print(node.key + ' '); preOrder(node.left); preOrder(node.right); } } public static void main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ System.out.println('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed by Mayank Jaiswal> |
>
>
Python3
# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif> key root.left = self.insert(root.left, key) else: root.right = self.insert(root.right, key) # Step 2 - Update the height of the # ancestor node root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right)) # Step 3 - Get the balance factor balance = self.getBalance(root) # Step 4 - If the node is unbalanced, # then try out the 4 cases # Case 1 - Left Left if balance>1 und Taste return self.rightRotate(root) # Fall 2 – Rechts Rechts bei Gleichgewicht<-1 and key>root.right.val: return self.leftRotate(root) # Fall 3 – Links rechts, wenn Balance> 1 und key> root.left.val: root.left = self.leftRotate(root.left) return self.rightRotate(root ) # Fall 4 – Rechts Links bei Gleichgewicht<-1 and key root.right = self.rightRotate(root.right) return self.leftRotate(root) return root def leftRotate(self, z): y = z.right T2 = y.left # Perform rotation y.left = z z.right = T2 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def rightRotate(self, z): y = z.left T3 = y.right # Perform rotation y.right = z z.left = T3 # Update heights z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right)) y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right)) # Return the new root return y def getHeight(self, root): if not root: return 0 return root.height def getBalance(self, root): if not root: return 0 return self.getHeight(root.left) - self.getHeight(root.right) def preOrder(self, root): if not root: return print('{0} '.format(root.val), end='') self.preOrder(root.left) self.preOrder(root.right) # Driver program to test above function myTree = AVL_Tree() root = None root = myTree.insert(root, 10) root = myTree.insert(root, 20) root = myTree.insert(root, 30) root = myTree.insert(root, 40) root = myTree.insert(root, 50) root = myTree.insert(root, 25) '''The constructed AVL Tree would be 30 / 20 40 / 10 25 50''' # Preorder Traversal print('Preorder traversal of the', 'constructed AVL tree is') myTree.preOrder(root) print() # This code is contributed by Ajitesh Pathak> |
>
>
C#
// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>B) ? a : b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); else // Doppelte Schlüssel nicht zulässig return node; /* 2. Höhe dieses Vorgängerknotens aktualisieren */ node.height = 1 + max(height(node.left), height(node.right)); /* 3. Holen Sie sich den Gleichgewichtsfaktor dieses Vorgängerknotens, um zu prüfen, ob dieser Knoten unausgeglichen ist */ int balance = getBalance(node); // Wenn dieser Knoten unausgeglichen wird, gibt es // 4 Fälle Left Left Case if (balance> 1 && key return rightRotate(node); // Right Right Case if (balance node.right.key) return leftRotate(node) ; // Left Right Case if (balance> 1 && key> node.left.key) { node.left = leftRotate(node } // Right Left Rotate(node);<-1 && key < node.right.key) { node.right = rightRotate(node.right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node void preOrder(Node node) { if (node != null) { Console.Write(node.key + ' '); preOrder(node.left); preOrder(node.right); } } // Driver code public static void Main(String[] args) { AVLTree tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ Console.Write('Preorder traversal' + ' of constructed tree is : '); tree.preOrder(tree.root); } } // This code has been contributed // by PrinciRaj1992> |
>
>
Javascript
> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>B ? a : b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if> (key node.left = this.insert(node.left, key); else if (key>node.key) node.right = this.insert(node.right, key); // Doppelte Schlüssel nicht erlaubt, sonst return node; /* 2. Höhe dieses Vorgängerknotens aktualisieren */ node.height = 1 + this.max(this.height(node.left), this.height(node.right)); /* 3. Holen Sie sich den Gleichgewichtsfaktor dieses Vorgängerknotens, um zu prüfen, ob dieser Knoten unausgeglichen ist */ var balance = this.getBalance(node); // Wenn dieser Knoten unausgeglichen wird, gibt es // 4 Fälle Left Left Case if (balance> 1 && key return this.rightRotate(node); // Right Right Case if (balance node.right.key) return this. leftRotate(node); // Left Right Case if (balance> 1 && key> node.left.key) { node.left = this.leftRotate(node.left); return this.rightRotate(node); Linker Fall, wenn (Balance<-1 && key < node.right.key) { node.right = this.rightRotate(node.right); return this.leftRotate(node); } /* return the (unchanged) node pointer */ return node; } // A utility function to print preorder traversal // of the tree. // The function also prints height of every node preOrder(node) { if (node != null) { document.write(node.key + ' '); this.preOrder(node.left); this.preOrder(node.right); } } } // Driver code var tree = new AVLTree(); /* Constructing tree given in the above figure */ tree.root = tree.insert(tree.root, 10); tree.root = tree.insert(tree.root, 20); tree.root = tree.insert(tree.root, 30); tree.root = tree.insert(tree.root, 40); tree.root = tree.insert(tree.root, 50); tree.root = tree.insert(tree.root, 25); /* The constructed AVL Tree would be 30 / 20 40 / 10 25 50 */ document.write( 'Preorder traversal of the ' + 'constructed AVL tree is ' ); tree.preOrder(tree.root);> |
>
>Ausgabe
Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>
Komplexitätsanalyse
Zeitkomplexität: O(log(n)), zum Einfügen
Hilfsraum: O(1)
Schaltfläche im mittleren CSS
Die Rotationsvorgänge (Links- und Rechtsdrehung) benötigen eine konstante Zeit, da dort nur wenige Zeiger geändert werden. Das Aktualisieren der Höhe und das Ermitteln des Ausgleichsfaktors nehmen ebenfalls eine konstante Zeit in Anspruch. Die zeitliche Komplexität der AVL-Einfügung bleibt also dieselbe wie die der BST-Einfügung, die O(h) ist, wobei h die Höhe des Baums ist. Da der AVL-Baum ausgeglichen ist, beträgt die Höhe O(Logn). Die zeitliche Komplexität der AVL-Einfügung beträgt also O(Logn).
Vergleich mit Rot-Schwarz-Baum:
Der AVL-Baum und andere selbstausgleichende Suchbäume wie Red Black sind nützlich, um alle grundlegenden Operationen in O(log n)-Zeit auszuführen. Die AVL-Bäume sind im Vergleich zu Rot-Schwarz-Bäumen ausgeglichener, verursachen jedoch möglicherweise mehr Rotationen beim Einfügen und Löschen. Wenn Ihre Anwendung also viele häufige Einfügungen und Löschungen beinhaltet, sollten Rot-Schwarz-Bäume bevorzugt werden. Und wenn die Einfügungen und Löschungen seltener sind und die Suche die häufigere Operation ist, sollte der AVL-Baum dem Red Black Tree vorgezogen werden.
Es folgt der Beitrag zum Löschen im AVL-Baum:
AVL-Baum | Satz 2 (Löschung)
