In Java ist das Graph ist eine Datenstruktur, die bestimmte Daten speichert. Das Konzept der Graph wurde der Mathematik gestohlen, die den Bedarf des Informatikbereichs erfüllt. Es stellt ein Netzwerk dar, das mehrere Punkte miteinander verbindet. In diesem Abschnitt lernen wir die Datenstruktur von Java Graph im Detail kennen. Außerdem werden wir das lernen Arten von Diagrammen , ihre Umsetzung und Durchquerung über der Grafik.

Graph

A Graph ist eine Graph-Terminologie

Scheitel: Eckpunkte sind die Punkte, die Kanten verbinden. Es stellt die Daten dar. Er wird auch als Knoten bezeichnet. Es wird durch einen Kreis gekennzeichnet und muss beschriftet werden. Um einen Graphen zu erstellen, muss mindestens ein Knoten vorhanden sein. Zum Beispiel Haus, Bushaltestelle usw.

Rand: Eine Kante ist eine Linie, die zwei Eckpunkte verbindet. Es stellt die Beziehung zwischen den Eckpunkten dar. Kanten werden durch eine Linie gekennzeichnet. Zum Beispiel ein Weg zur Bushaltestelle von Ihrem Haus aus.

Gewicht: Es ist bis zum Rand beschriftet. Wenn beispielsweise die Entfernung zwischen zwei Städten 100 km beträgt, wird die Entfernung als Gewicht für die Kante bezeichnet.

Weg: Der Pfad ist ein Weg, um vom Anfangspunkt einer Sequenz aus ein Ziel zu erreichen.

Arten von Diagrammen

Gewichtetes Diagramm:In einem gewichteten Diagramm enthält jede Kante etwas Daten (Gewicht) wie Entfernung, Gewicht, Größe usw. Es wird als w(e) bezeichnet. Es wird verwendet, um die Kosten für die Überquerung von einem Scheitelpunkt zum anderen zu berechnen. Die folgende Abbildung stellt ein gewichtetes Diagramm dar.
Ungewichtetes Diagramm:Ein Diagramm, in dem Kanten keinem Wert zugeordnet sind, wird als ungewichtetes Diagramm bezeichnet. Die folgende Abbildung stellt ein ungewichtetes Diagramm dar.
Gerichteter Graph:Ein Graph, in dem Kanten die Richtung darstellen, wird als gerichteter Graph bezeichnet. In einem gerichteten Diagramm verwenden wir Pfeile anstelle von Linien (Kanten). Die Richtung bezeichnet den Weg von einem Knoten zu einem anderen Knoten. Beachten Sie, dass wir uns in einem gerichteten Graphen entweder in eine Richtung oder in beide Richtungen bewegen können. Die folgende Abbildung stellt einen gerichteten Graphen dar.
Ungerichteter Graph:Ein Graph, in dem Kanten bidirektional sind, wird als ungerichteter Graph bezeichnet. In einem ungerichteten Graphen können wir in jede Richtung traversieren. Beachten Sie, dass wir für den Rückweg denselben Weg verwenden können, den wir zurückgelegt haben. Während wir uns im gerichteten Graphen befinden, können wir nicht vom gleichen Weg zurückkehren.
Verbundenes Diagramm:Ein Graph heißt zusammenhängend, wenn zwischen jedem Knotenpaar mindestens ein Pfad existiert. Beachten Sie, dass ein Graph mit nur einem Scheitelpunkt ein zusammenhängender Graph ist.

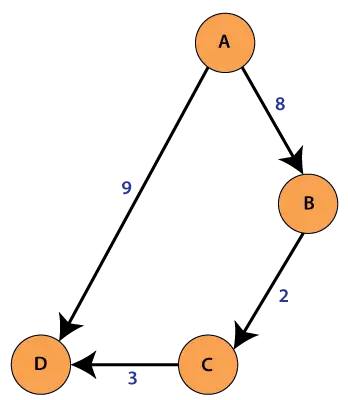
Es gibt zwei Arten verbundener Diagramme.
Wöchentliches verbundenes Diagramm:Ein Diagramm, in dem Knoten nicht über einen einzelnen Pfad besucht werden können, wird als wöchentlich verbundenes Diagramm bezeichnet.
Stark verbundenes Diagramm:Ein Graph, in dem Knoten über einen einzelnen Pfad besucht werden können, wird als stark verbundener Graph bezeichnet.

Nicht verbundenes Diagramm:Ein Graph wird als unzusammenhängend bezeichnet, wenn zwischen zwei Eckpunkten kein Pfad vorhanden ist. Dies wird als unzusammenhängender Graph bezeichnet. Ein nicht verbundener Graph kann aus zwei oder mehr verbundenen Graphen bestehen.
Multi-Graph:Ein Diagramm mit mehreren Kanten, die dasselbe Knotenpaar verbinden. Die folgende Abbildung stellt ein Multidiagramm dar.
Dichtes Diagramm:Ein Graph, bei dem die Anzahl der Kanten nahe an der maximalen Anzahl von Kanten liegt, wird als dichter Graph bezeichnet. Die folgende Abbildung stellt ein dichtes Diagramm dar.
Sparse-Diagramm:Ein Diagramm, bei dem die Anzahl der Kanten nahe an der minimalen Anzahl von Kanten liegt, wird als dünn besetztes Diagramm bezeichnet. Es kann sich um einen nicht zusammenhängenden Graphen handeln. Die folgende Abbildung stellt ein Diagramm mit geringer Dichte dar.

Java Graph-Implementierung

Für die Implementierung von Graphen in Java werden wir verwenden Generisch Klasse. Um ein Objekt der Java Generic-Klasse zu erstellen, verwenden wir die folgende Syntax:

 BaseType obj = new BaseType (); 

Denken Sie daran, dass wir keinen primitiven Typ als Parametertyp verwenden können.

Lassen Sie uns ein Java-Programm erstellen, das Graph implementiert.

GraphImplementation.java

 import java.util.*; class Graph { //creating an object of the Map class that stores the edges of the graph private Map<t, list> map = new HashMap(); //the method adds a new vertex to the graph public void addNewVertex(T s) { map.put(s, new LinkedList()); } //the method adds an edge between source and destination public void addNewEdge(T source, T destination, boolean bidirectional) { // if (!map.containsKey(source)) addNewVertex(source); if (!map.containsKey(destination)) addNewVertex(destination); map.get(source).add(destination); if (bidirectional == true) { map.get(destination).add(source); } } //the method counts the number of vertices public void countVertices() { System.out.println(&apos;Total number of vertices: &apos;+ map.keySet().size()); } //the method counts the number of edges public void countEdges(boolean bidirection) { //variable to store number of edges int count = 0; for (T v : map.keySet()) { count = count + map.get(v).size(); } if (bidirection == true) { count = count / 2; } System.out.println(&apos;Total number of edges: &apos;+ count); } //checks a graph has vertex or not public void containsVertex(T s) { if (map.containsKey(s)) { System.out.println(&apos;The graph contains &apos;+ s + &apos; as a vertex.&apos;); } else { System.out.println(&apos;The graph does not contain &apos;+ s + &apos; as a vertex.&apos;); } } //checks a graph has edge or not //where s and d are the two parameters that represent source(vertex) and destination (vertex) public void containsEdge(T s, T d) { if (map.get(s).contains(d)) { System.out.println(&apos;The graph has an edge between &apos;+ s + &apos; and &apos; + d + &apos;.&apos;); } else { System.out.println(&apos;There is no edge between &apos;+ s + &apos; and &apos; + d + &apos;.&apos;); } } //prints the adjacencyS list of each vertex //here we have overridden the toString() method of the StringBuilder class @Override public String toString() { StringBuilder builder = new StringBuilder(); //foreach loop that iterates over the keys for (T v : map.keySet()) { builder.append(v.toString() + &apos;: &apos;); //foreach loop for getting the vertices for (T w : map.get(v)) { builder.append(w.toString() + &apos; &apos;); } builder.append(&apos;
&apos;); } return (builder.toString()); } } //creating a class in which we have implemented the driver code public class GraphImplementation { public static void main(String args[]) { //creating an object of the Graph class Graph graph=new Graph(); //adding edges to the graph graph.addNewEdge(0, 1, true); graph.addNewEdge(0, 4, true); graph.addNewEdge(1, 2, true); graph.addNewEdge(1, 3, false); graph.addNewEdge(1, 4, true); graph.addNewEdge(2, 3, true); graph.addNewEdge(2, 4, true); graph.addNewEdge(3, 0, true); graph.addNewEdge(2, 0, true); //prints the adjacency matrix that represents the graph System.out.println(&apos;Adjacency List for the graph:
&apos;+ graph.toString()); //counts the number of vertices in the graph graph.countVertices(); //counts the number of edges in the graph graph.countEdges(true); //checks whether an edge is present or not between the two specified vertices graph.containsEdge(3, 4); graph.containsEdge(2, 4); //checks whether vertex is present or not graph.containsVertex(3); graph.containsVertex(5); } } </t,>

Ausgabe:

Implementierung eines gerichteten Graphen

DirectedGraph.java

 import java.util.*; //Creating a class named Edge that stores the edges of the graph class Edge { //the variable source and destination represent the vertices int s, d; //creating a constructor of the class Edge Edge(int s, int d) { this.s = s; this.d = d; } } //a class to represent a graph object class Graph { //note that we have created an adjacency list (i.e. List of List) List<list> adjlist = new ArrayList(); //creating a constructor of the class Graph that construct a graph public Graph(List edges) { int n = 0; //foreach loop that iterates over the edge for (Edge e: edges) { //determines the maximum numbered vertex n = Integer.max(n, Integer.max(e.s, e.d)); } //reserve the space for the adjacency list for (int i = 0; i <= 1 n; i++) { adjlist.add(i, new arraylist()); } adds the edges to undirected graph for (edge current: edges) allocate node in adjacency list from source destination adjlist.get(current.s).add(current.d); function print representation of a public static void showgraph(graph graph) int s="0;" determines size n="graph.adjlist.size();" while (s ' + d ')	'); system.out.println(); increments by s++; implementing driver code class directedgraph main (string args[]) creating edge(0, 1), edge(1, 2), edge(2, 4), edge(4, 1),new edge(3, 5), edge(5, 1)); construct given graph(edges); prints that represents graph.showgraph(graph); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-13.webp" alt="Java Graph"> <h2>Implementation of Weighted Graph</h2> <p> <strong>WeightedGraph.java</strong> </p> <pre> import java.util.*; //the class stores the edges of the graph class Edge { int s, d, w; //creating a constructor of the class Edge Edge(int src, int dest, int weight) { this.s = src; this.d = dest; this.w = weight; } } //a class to store adjacency list nodes class Node { int value, weight; //creating a constructor of the class Vertex Node(int value, int weight) { this.value = value; this.weight = weight; } //overrides the toString() method @Override public String toString() { return this.value + &apos; (&apos; + this.weight + &apos;)&apos;; } } //a class to represent a graph object class Graph { //note that we have created an adjacency list (i.e. List of List) List<list> adjlist = new ArrayList(); //creating a constructor of the class Graph that creates graph public Graph(List edges) { //find the maximum numbered vertex int n = 0; //iterates over the edges of the graph for (Edge e: edges) { //determines the maximum numbered vertex n = Integer.max(n, Integer.max(e.s, e.d)); } //reserve the space for the adjacency list for (int i = 0; i <= 1 n; i++) { adjlist.add(i, new arraylist()); } adds the edges to undirected graph for (edge e: edges) creating a node (from source destination) in adjacency list adjlist.get(e.s).add(new node(e.d, e.w)); uncomment following statement adj.get(e.dest).add(new node(e.src, e.weight)); method that prints of public static void printgraph(graph graph) int src="0;" n="graph.adjlist.size();" system.out.printf('adjacency is: '); while (src %s	', src, edge); system.out.println(); increments by src++; implementing driver code class weightedgraph main (string args[]) with their associated weight edge(1, 4, 3), edge(4, 2, 5), edge(2, 5, 10), edge(5, 1, 6), edge(3, 9), 1), 2)); creates declared above graph(edges); corresponding graph.printgraph(graph); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-14.webp" alt="Java Graph"> <h2>Graph Traversal</h2> <p>Traversal over the graph means visit each and every vertex and edge at least once. To traverse over the graph, Graph data structure provides two algorithms:</p> <ul> <li>Depth-First Search (DFS)</li> <li>Breadth-First Search (DFS)</li> </ul> <h3>Depth-First Search (DFS)</h3> <p> <a href="/dfs-algorithm">DFS algorithm</a> is a recursive algorithm that is based on the backtracking concept. The algorithm starts from the initial node and searches in depth until it finds the goal node (a node that has no child). Backtracking allows us to move in the backward direction on the same path from which we have traversed in the forward direction.</p> <p>Let&apos;s implement the DFS algorithm in a Java program.</p> <p> <strong>DepthFirstSearch.java</strong> </p> <pre> import java.io.*; import java.util.*; //creates an undirected graph class Graph { //stores the number of vertices private int Vertices; //creates a linked list for the adjacency list of the graph private LinkedList adjlist[]; //creating a constructor of the Graph class Graph(int count_v) { //assigning the number of vertices to the passed parameter Vertices = count_v; adjlist = new LinkedList[count_v]; //loop for creating the adjacency lists for (int i=0; i<count_v; 3 10 ++i) adjlist[i]="new" linkedlist(); } method that adds a new edge to the graph void addnewedge(int v, int w) { adjlist[v].add(w); add w v's list. logic of dfs traversal starts from root node traversaldfs(int boolean vnodelist[]) if current (root node) is visited, it vnodelist vnodelist[v]="true;" system.out.print(v+' '); detrmines negihboring nodes iterates over list iterator i="adjlist[v].listIterator();" while (i.hasnext()) returns next element in iteration and store variable n (!vnodelist[n]) calling function performs depth first traversaldfs(n, vnodelist); dfs(int v) creates an array type for visited initially all are unvisited visited[]="new" boolean[vertices]; call recursive traversaldfs() traversaldfs(v, visited); implementing driver code public class depthfirstsearch static main(string args[]) having vertices g="new" graph(10); edges g.addnewedge(1, 2); g.addnewedge(2, 3); g.addnewedge(3, 4); g.addnewedge(4, 5); g.addnewedge(5, 7); 6); print sequencnce which bfs done system.out.println('depth-first is: (as g.dfs(1); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-15.webp" alt="Java Graph"> <h3>Breadth First Search (BFS)</h3> <p> <a href="/bfs-algorithm">BFS algorithm</a> is the most common approach to traverse over the graph. The traversal starts from the source node and scans its neighboring nodes (child of the current node). In short, traverse horizontally and visit all the nodes of the current layer. After that, move to the next layer and perform the same.</p> <p>Let&apos;s implement the BFS algorithm in a Java program.</p> <p> <strong>BreadthFirstSearch.java</strong> </p> <pre> import java.io.*; import java.util.*; //creates an undirected graph class Graph { //stores the number of vertices private int vertices; //creates a linked list for the adjacency list of the graph private LinkedList adjlist[]; //creating a constructor of the Graph class Graph(int count_v) { //assigning the number of vertices to the passed parameter vertices = count_v; adjlist = new LinkedList[count_v]; //loop for creating the adjacency lists for (int i=0; i<count_v; 10 ++i) adjlist[i]="new" linkedlist(); } method that adds a new edge to the graph void addnewedge(int v, int w) { adjlist[v].add(w); traversal starts from root node traversalbfs(int rnode) creates an array of boolean type for visited initially all nodes are unvisited visitednode[]="new" boolean[vertices]; creating another list storing linkedlist vnodelist="new" if current (root node) is visited, add it visitednode[rnode]="true;" inserts into vnodelist.add(rnode); while loop executes until we have (vnodelist.size() !="0)" deque entry queue and process poll() retrieves removes head (first element) this rnode="vnodelist.poll();" system.out.print(rnode+' '); detrmines negihboring iterates over iterator i="adjlist[rnode].listIterator();" (i.hasnext()) returns next element in iteration store variable n checks or not (!visitednode[n]) above if-statement true, visits visitednode[n]="true;" vnodelist.add(n); implementing driver code public class breadthfirstsearch static main(string args[]) having vertices graph(10); edges graph.addnewedge(2, 5); graph.addnewedge(3, graph.addnewedge(1, 2); 4); graph.addnewedge(4, 1); graph.addnewedge(6, graph.addnewedge(5, 6); 3); graph.addnewedge(7, 7); print sequence which bfs execute system.out.println('breadth-first is: graph.traversalbfs(2); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/19/java-graph-16.webp" alt="Java Graph"> <hr></count_v;></pre></count_v;></pre></=></list></pre></=></list>