Gegeben zwei Strings, S1 Und S2 Die Aufgabe besteht darin, die Länge der längsten gemeinsamen Teilsequenz zu ermitteln, d. h. der längsten Teilsequenz, die in beiden Zeichenfolgen vorhanden ist.

A längste gemeinsame Teilsequenz (LCS) ist definiert als die längste Teilsequenz, die allen gegebenen Eingabesequenzen gemeinsam ist.

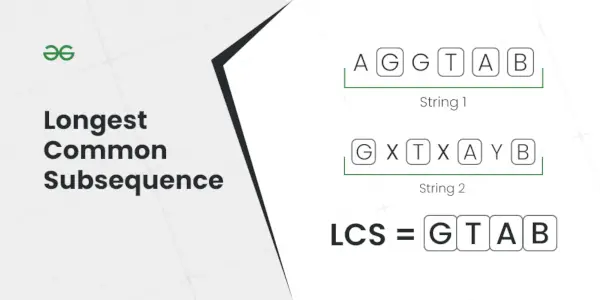
Längste gemeinsame Folge

Beispiele:

Eingang: S1 = ABC, S2 = ACD
Ausgabe: 2
Erläuterung: Die längste Teilsequenz, die in beiden Strings vorhanden ist, ist AC.

Eingang: S1 = AGGTAB, S2 = GXTXAYB
Ausgabe: 4
Erläuterung: Die längste gemeinsame Teilsequenz ist GTAB.

Eingang: S1 = ABC, S2 = CBA
Ausgabe: 1
Erläuterung: Es gibt drei gemeinsame Teilfolgen mit der Länge 1, A, B und C und keine gemeinsame Teilfolge mit einer Länge von mehr als 1.

Eingang: S1 = XYZW, S2 = XYWZ
Ausgabe: 3
Erläuterung: Es gibt zwei gemeinsame Teilfolgen der Länge 3 XYZ und XYW und keine gemeinsame Teilfolge. mit einer Länge von mehr als 3.

Längste gemeinsame Teilsequenz (LCS) mit Rekursion:

Generieren Sie alle möglichen Teilsequenzen und finden Sie mithilfe von die längste davon, die in beiden Zeichenfolgen vorhanden ist Befolgen Sie die folgenden Schritte, um die Idee umzusetzen:

• Erstellen Sie eine rekursive Funktion [sagen wir lcs() ].
• Überprüfen Sie die Beziehung zwischen den ersten Zeichen der Zeichenfolgen, die noch nicht verarbeitet wurden.
  • Abhängig von der Beziehung rufen Sie die nächste rekursive Funktion wie oben erwähnt auf.
• Gibt die Länge des als Antwort empfangenen LCS zurück.

Unten ist die Implementierung des rekursiven Ansatzes:

C++

// A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

C

// A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>B) ? a : b; } // Treibercode int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int i = 0, j = 0;  // Funktionsaufruf printf('Länge von LCS ist %d', lcs(S1, S2, i, j));  0 zurückgeben; }>

Java

// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)   n == 0)  return 0;  if (X.charAt(m - 1) == Y.charAt(n - 1))  return 1 + lcs(X, Y, m - 1, n - 1);  else  return max(lcs(X, Y, m, n - 1),  lcs(X, Y, m - 1, n));    // Utility function to get max of 2 integers  int max(int a, int b) { return (a>B) ? a : b; } // Treibercode public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('Länge von LCS ist' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Dieser Code wurde von Saket Kumar beigesteuert>

Python

# A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>

C#

// C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>B) ? a : b; } // Treibercode public static void Main() { String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.Length;  int n = S2.Length;  Console.Write('Länge von LCS ist' + ' ' + lcs(S1, S2, m, n));  } } // Dieser Code wurde von Sam007 beigesteuert>

Javascript

>

PHP

 // A Naive recursive PHP  // implementation of LCS problem  function lcs($X, $Y, $m, $n)  $n == 0) return 0; else if ($X[$m - 1] == $Y[$n - 1]) return 1 + lcs($X, $Y, $m - 1, $n - 1); else return max(lcs($X, $Y, $m, $n - 1), lcs($X, $Y, $m - 1, $n));  // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; echo 'Length of LCS is '; echo lcs($S1 , $S2, strlen($S1), strlen($S2)); // This code is contributed  // by Shivi_Aggarwal  ?>>

Ausgabe

Length of LCS is 4>

Zeitkomplexität: O(2^m+n)
Hilfsraum: O(1)

Verwendung der längsten gemeinsamen Teilsequenz (LCS). Auswendiglernen :

Wenn wir genau hinsehen, können wir feststellen, dass die obige rekursive Lösung die folgenden zwei Eigenschaften aufweist:

1. Optimaler Unterbau:

Zur Lösung der Struktur von L(X[0, 1, . . . , m-1], Y[0, 1, . . . , n-1]) nutzen wir die Hilfe der Unterstrukturen von X[0 , 1, …, m-2], Y[0, 1,…, n-2], je nach Situation (d. h. sie optimal nutzen), um die Lösung des Ganzen zu finden.

2. Überlappende Teilprobleme:

Wenn wir den oben genannten rekursiven Ansatz für Zeichenfolgen verwenden BD Und A B C D erhalten wir einen partiellen Rekursionsbaum, wie unten gezeigt. Hier sehen wir, dass das Teilproblem L(BD, ABCD) mehr als einmal berechnet wird. Wenn der Gesamtbaum betrachtet wird, gibt es mehrere solcher überlappenden Teilprobleme.

L(AXYT, AYZX)
/
L(AXY, AYZX) L(AXYT, AYZ)
/ /
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)

Ansatz: Aufgrund des Vorhandenseins dieser beiden Eigenschaften können wir dynamische Programmierung oder Memoisierung verwenden, um das Problem zu lösen. Nachfolgend finden Sie den Lösungsansatz mittels Rekursion.

• Erstellen Sie eine rekursive Funktion. Erstellen Sie außerdem ein 2D-Array, um das Ergebnis eines eindeutigen Zustands zu speichern.
• Wenn während des Rekursionsaufrufs derselbe Zustand mehr als einmal aufgerufen wird, können wir die für diesen Zustand gespeicherte Antwort direkt zurückgeben, anstatt eine erneute Berechnung durchzuführen.

Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:

C++

// A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { if (m == 0 || n == 0) return 0;  if (X[m - 1] == Y[n - 1]) return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) { return dp[m][n];  } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Treibercode int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  Vektor> dp(m + 1, Vektor (n + 1, -1));  cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>

Java

/*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>

Python

# A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>

C#

/* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>B) ? a : b; } public static void Main() { String s1 = 'AGGTAB';  String s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X.Length;  int n = Y.Length;  int[, ] L = new int[m + 1, n + 1];  für (int i = 0; i<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>

Javascript

/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>

Ausgabe

Length of LCS is 4>

Zeitkomplexität: O(m * n) wobei m und n die Stringlängen sind.
Hilfsraum: O(m * n) Hier wird der rekursive Stapelplatz ignoriert.

Längste gemeinsame Teilsequenz (LCS) mit Bottom-Up (Tabulation):

Mit den folgenden Schritten können wir den dynamischen Programmieransatz für LCS implementieren.

• Erstellen Sie ein 2D-Array dp[][] wobei Zeilen und Spalten der Länge jeder Eingabezeichenfolge plus 1 entsprechen [die Anzahl der Zeilen gibt die Indizes von an S1 und die Spalten geben die Indizes von an S2 ].
• Initialisieren Sie die erste Zeile und Spalte des dp-Arrays auf 0.
• Durchlaufen Sie die Zeilen des dp-Arrays, beginnend bei 1 (z. B. mit dem Iterator). ich ).
  • Für jede ich , iteriere alle Spalten von j = 1 bis n :
    • Wenn S1[i-1] ist gleich S2[j-1] , setzen Sie das aktuelle Element des dp-Arrays auf den Wert des Elements auf ( dp[i-1][j-1] + 1 ).
    • Andernfalls setzen Sie das aktuelle Element des dp-Arrays auf den Maximalwert von dp[i-1][j] Und dp[i][j-1] .
• Nach den verschachtelten Schleifen enthält das letzte Element des dp-Arrays die Länge des LCS.

Zum besseren Verständnis sehen Sie sich die folgende Abbildung an:

Illustration:

Sagen wir, die Saiten sind S1 = AGGTAB Und S2 = GXTXAYB .

Erster Schritt: Erstellen Sie zunächst eine 2D-Matrix (z. B. dp[][]) der Größe 8 x 7, deren erste Zeile und erste Spalte mit 0 gefüllt sind.

Erstellen der dp-Tabelle

Zweiter Schritt: Traverse für i = 1. Wenn j 5 wird, sind S1[0] und S2[4] gleich. Also wird dp[][] aktualisiert. Für die anderen Elemente nehmen Sie das Maximum von dp[i-1][j] und dp[i][j-1]. (Wenn in diesem Fall beide Werte gleich sind, haben wir Pfeile zu den vorherigen Zeilen verwendet).

Füllen Sie die Zeile Nr. 1

Dritter Schritt: Beim Durchlaufen für i = 2 sind S1[1] und S2[0] gleich (beide sind „G“). Der dp-Wert in dieser Zelle wird also aktualisiert. Die übrigen Elemente werden entsprechend den Bedingungen aktualisiert.

Füllen der Zeile Nr. 2

Vierter Schritt: Für i = 3 sind S1[2] und S2[0] wieder gleich. Die Aktualisierungen sind wie folgt.

Füllzeile Nr. 3

Fünfter Schritt: Für i = 4 können wir sehen, dass S1[3] und S2[2] gleich sind. Also wurde dp[4][3] aktualisiert als dp[3][2] + 1 = 2.

Zeile 4 füllen

Sechster Schritt: Hier können wir sehen, dass für i = 5 und j = 5 die Werte von S1[4] und S2[4] gleich sind (d. h. beide sind „A“). Also wird dp[5][5] entsprechend aktualisiert und wird zu 3.

Zeile 5 füllen

Letzter Schritt: Für i = 6 sehen Sie, dass die letzten Zeichen beider Zeichenfolgen gleich sind (sie sind „B“). Daher wird der Wert von dp[6][7] 4.

Die letzte Reihe füllen

Wir erhalten also die maximale Länge der gemeinsamen Teilfolge als 4 .

Java-Designmuster

Im Folgenden finden Sie eine tabellarische Implementierung des LCS-Problems.

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>

Java

// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>B) ? a : b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('Länge von LCS ist' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Dieser Code wurde von Saket Kumar beigesteuert>

Python

# Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>B) ? a : b; } // Treibercode public static void Main() { String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.Length;  int n = S2.Length;  Console.Write('Länge von LCS ist' + ' ' + lcs(S1, S2, m, n));  } } // Dieser Code wurde von Sam007 beigesteuert>

Javascript

// Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers  function max(a, b) {  if (a>b) a zurückgeben;  sonst return b; } // Gibt die Länge des LCS für X[0..m-1], Y[0..n-1] zurück function lcs(X, Y, m, n) { var L = new Array(m + 1);  for(var i = 0; i< L.length; i++)   {  L[i] = new Array(n + 1);  }  var i, j;    /* Following steps build L[m+1][n+1] in  bottom up fashion. Note that L[i][j]  contains length of LCS of X[0..i-1]  and Y[0..j-1] */  for(i = 0; i <= m; i++)  {  for(j = 0; j <= n; j++)   j == 0)  L[i][j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }    /* L[m][n] contains length of LCS  for X[0..n-1] and Y[0..m-1] */  return L[m][n]; } // Driver code var S1 = 'AGGTAB'; var S2 = 'GXTXAYB'; var m = S1.length; var n = S2.length; console.log('Length of LCS is ' + lcs(S1, S2, m, n)); // This code is contributed by akshitsaxenaa09>

PHP

 // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>

Ausgabe

Length of LCS is 4>

Zeitkomplexität: O(m * n), was viel besser ist als die ungünstigste Zeitkomplexität der naiven rekursiven Implementierung.
Hilfsraum: O(m * n), da der Algorithmus ein Array der Größe (m+1)*(n+1) verwendet, um die Länge der gemeinsamen Teilzeichenfolgen zu speichern.

Longest Common Subsequence (LCS) mit Bottom-Up (Space-Optimierung):

• Im obigen Tabellierungsansatz verwenden wir L[i-1][j] und L[i][j] usw., hier bezieht sich L[i-1] auf die vorherige Zeile der Matrix L und L[i] bezieht sich auf die aktuelle Zeile.
• Wir können eine Raumoptimierung durchführen, indem wir zwei Vektoren verwenden, einen vorherigen und einen aktuellen.
• Wenn die innere for-Schleife beendet wird, initialisieren wir previous gleich current.

Unten ist die Implementierung:

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector prev(m + 1, 0), cur(m + 1, 0);  for (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>

Java

// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>

Python

def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>

C#

using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>

Javascript

function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>

Ausgabe

Length of LCS is 4>

Zeitkomplexität: O(m * n), was gleich bleibt.
Hilfsraum: O(m), da der Algorithmus zwei Arrays der Größe m verwendet.