Der Begriff Auswendiglernen kommt vom lateinischen Wort Memorandum ( erinnern ), was im amerikanischen Englisch üblicherweise als Memo abgekürzt wird und bedeutet, die Ergebnisse einer Funktion in etwas umzuwandeln, an das man sich erinnern kann.
Beim Rechnen wird Memoisierung verwendet, um Computerprogramme zu beschleunigen, indem die wiederholte Berechnung von Ergebnissen entfällt und wiederholte Aufrufe von Funktionen vermieden werden, die dieselben Eingaben verarbeiten.

Was ist Auswendiglernen?
Inhaltsverzeichnis
- Was ist Auswendiglernen?
- Warum wird die Memoisierung verwendet?
- Wo kann Memoization verwendet werden?
- Arten der Memoisierung
- Wie wird die Memoisierungstechnik in der dynamischen Programmierung verwendet?
- Wie unterscheidet sich das Auswendiglernen von der Tabellierung?
- Codierungsübungsprobleme für das Auswendiglernen
- FAQs
- 1) Ist Auswendiglernen besser als DP?
- 2) Ist das Auswendiglernen dasselbe wie das Zwischenspeichern?
- 3) Warum erfolgt das Auswendiglernen von oben nach unten?
- 4) Verwendet das Auswendiglernen eine Rekursion?
- 5) Sollte ich Tabellierung oder Memoisierung verwenden?
- 6) Wo wird das Auswendiglernen verwendet?
- 7) Warum heißt es Auswendiglernen?
- 8) Wie reduziert das Auswendiglernen die Zeitkomplexität?
- 9) Was ist der Unterschied zwischen Memoisierung und Caching?
- 10) Warum ist das Tabellieren schneller als das Auswendiglernen?
- Abschluss
Warum wird Memoisierung verwendet?
Auswendiglernen ist eine spezielle Form von Caching das wird in verwendet dynamische Programmierung . Der Zweck des Caching besteht darin, die Leistung unserer Programme zu verbessern und Daten zugänglich zu halten, die später verwendet werden können. Grundsätzlich wird das zuvor berechnete Ergebnis des Teilproblems gespeichert und das gespeicherte Ergebnis für dasselbe Teilproblem verwendet. Dadurch entfällt der zusätzliche Aufwand, für dasselbe Problem immer wieder Berechnungen anzustellen. Und wir wissen bereits, dass, wenn dasselbe Problem immer wieder auftritt, dieses Problem rekursiver Natur ist.
Wo kann Memoization verwendet werden?
Wir können die Memoisierungstechnik verwenden, bei der die Verwendung der zuvor berechneten Ergebnisse kommt ins Bild. Diese Art von Problem wird meist im Zusammenhang mit verwendet Rekursion , insbesondere bei Problemen, die damit verbunden sind überlappende Teilprobleme .
Nehmen wir ein Beispiel, bei dem sich dasselbe Teilproblem immer wieder wiederholt.
Beispiel, um zu zeigen, wo Memoisierung verwendet werden kann:
Let us try to find the factorial of a number .>
Unten ist ein rekursive Methode um die Fakultät einer Zahl zu finden:
int faktoriell(unsigned int n)
{
wenn (n == 0)
Rückgabe 1;
return n * Faculty(n – 1);
}
Was passiert, wenn wir diese rekursive Methode verwenden?
Wenn Sie den vollständigen Code für das obige Snippet schreiben, werden Sie feststellen, dass der Code zwei Methoden enthält:
1. factorial(n) 2. main()>
Wenn wir nun mehrere Abfragen haben, um die Fakultät zu finden, beispielsweise die Fakultät 2, 3, 9 und 5, müssen wir die Methode „factorial()“ viermal aufrufen:
factorial(2) factorial(3) factorial(9) factorial(5)>
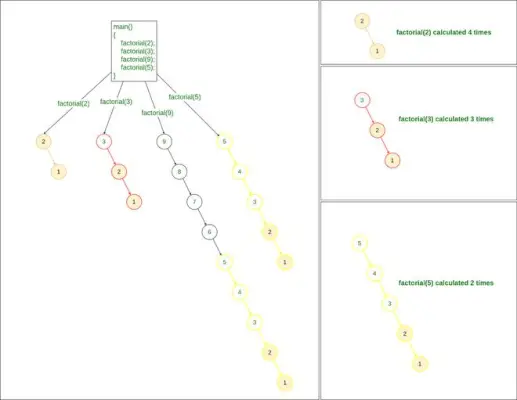
Rekursive Methode zum Finden von Factorial
Man kann also mit Sicherheit sagen, dass die erforderliche Zeitkomplexität zum Finden der Fakultät der Zahlen K erforderlich ist O(N*K)
- AN) die Fakultät einer bestimmten Zahl finden und
- PFEIL) um die Methode „factorial()“ K verschiedene Male aufzurufen.
Wie kann das Auswendiglernen bei solchen Problemen helfen?
Wenn wir im obigen Problem feststellen, dass die Fakultät 9 berechnet wird:
Java Double zum String
- Wir berechnen die Fakultät von 2
- Wir berechnen auch die Fakultät von 3,
- und wir berechnen auch die Fakultät von 5
Wenn wir also das Ergebnis jeder einzelnen Fakultät beim ersten Berechnungszeitpunkt speichern, können wir die Fakultät jeder erforderlichen Zahl problemlos in nur O(1)-Zeit zurückgeben. Dieser Vorgang ist bekannt als Auswendiglernen .
Lösung mit Memoisierung (Wie funktioniert Memoisierung?):
Wenn wir zuerst die Fakultät von 9 finden und die Ergebnisse einzelner Teilprobleme speichern, können wir die Fakultät jeder Eingabe in O(1) einfach ausdrucken.
Daher wird die Zeitkomplexität zum Finden von Fakultätszahlen mithilfe der Memoisierung groß sein AN)
- AN) um die Fakultät des größten Inputs zu finden
- O(1) um die Fakultät jeder Eingabe auszudrucken.
Arten der Memoisierung
Die Implementierung der Memoisierung hängt von den sich ändernden Parametern ab, die für die Lösung des Problems verantwortlich sind. Es gibt verschiedene Dimensionen des Cachings, die in der Memoisierungstechnik verwendet werden. Im Folgenden sind einige davon aufgeführt:
- 1D-Memoisierung: Die rekursive Funktion, die nur ein Argument hat, dessen Wert nach jedem Funktionsaufruf nicht konstant war.
- 2D-Memoisierung: Die rekursive Funktion, die nur zwei Argumente hat, deren Wert nach jedem Funktionsaufruf nicht konstant war.
- 3D-Memoisierung : Die rekursive Funktion, die nur drei Argumente hat, deren Werte nach jedem Funktionsaufruf nicht konstant waren.
Wie wird die Memoisierungstechnik in der dynamischen Programmierung verwendet?
Dynamische Programmierung hilft dabei, Probleme mit überlappenden Teilproblemen und optimalen Unterstruktureigenschaften effizient zu lösen. Die Idee hinter der dynamischen Programmierung besteht darin, das Problem in kleinere Teilprobleme zu zerlegen und das Ergebnis für die zukünftige Verwendung zu speichern, wodurch die Notwendigkeit entfällt, das Ergebnis wiederholt zu berechnen.
Es gibt zwei Ansätze, eine dynamische Programmierlösung zu formulieren:
- Top-Down-Ansatz: Dieser Ansatz folgt dem Auswendiglernen Technik . Es besteht aus Rekursion Und Caching . In der Berechnung stellt Rekursion den Prozess des wiederholten Aufrufs von Funktionen dar, während sich Cache auf den Prozess der Speicherung von Zwischenergebnissen bezieht.
- Bottom-Up-Ansatz: Dieser Ansatz nutzt die Tabellierung Technik um die dynamische Programmierlösung zu implementieren. Es behandelt die gleichen Probleme wie zuvor, jedoch ohne Rekursion. Bei diesem Ansatz ersetzt die Iteration die Rekursion. Daher gibt es keinen Stapelüberlauffehler oder Overhead durch rekursive Prozeduren.
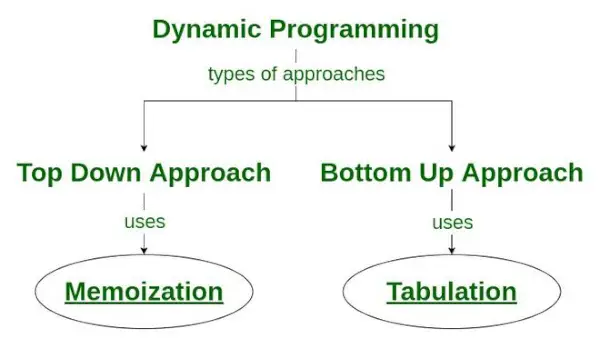
Wie die Memoisierungstechnik in der dynamischen Programmierung verwendet wird
Wie unterscheidet sich das Auswendiglernen von der Tabellierung?

Tabellierung vs. Auswendiglernen
Weitere Einzelheiten finden Sie unter: Tabellierung vs. Auswendiglernen
Probleme der Kodierungspraxis beim Auswendiglernen
| Frage | Artikel | Üben | Video |
|---|---|---|---|
| Zählen Sie die Wege, um die n-te Treppe zu erreichen | Sicht | Lösen | Betrachten |
| Wortbruchproblem | DP-32 | Sicht | Lösen | Betrachten |
| Programm für Fibonacci-Zahlen | Sicht | Lösen | Betrachten |
| n-te katalanische Zahl | Sicht | Lösen | Betrachten |
| Goldminenproblem | Sicht | Lösen | Betrachten |
| Teilmengensummenproblem | Sicht | Lösen | Betrachten |
| Eine Rute schneiden | Sicht | Lösen | Betrachten |
| Min. Kostenpfad | Sicht | Lösen | Betrachten |
| Mindestanzahl an Sprüngen, um das Ende zu erreichen | Sicht | Lösen | Betrachten |
| Längster palindromischer Teilstring | Set 1 | Sicht | Lösen | Betrachten |
| Längste sich wiederholende Teilsequenz | Sicht | Lösen | Betrachten |
| Zählen Sie die Wege, um mit Schritt 1, 2 oder 3 die n-te Treppe zu erreichen | Sicht | Lösen | Betrachten |
| Zählen Sie verschiedene Möglichkeiten, N als Summe von 1, 3 und 4 auszudrücken | Sicht | Lösen | Betrachten |
| Zählen Sie die Anzahl der Möglichkeiten, eine Strecke zurückzulegen Set vs. Karte | Sicht | Lösen | Betrachten |
| Anzahl der Arrays mit aufeinanderfolgenden Elementen mit unterschiedlichen Werten | Sicht | Lösen | Betrachten |
| Größte Summe zusammenhängender Subarray | Sicht | Lösen | Betrachten |
| Kleinste Summe zusammenhängender Subarrays | Sicht | Lösen | Betrachten |
| Einzigartige Wege in einem Raster mit Hindernissen | Sicht | Lösen | Betrachten |
| Verschiedene Möglichkeiten, n mithilfe von Zahlen größer oder gleich m zu summieren | Sicht | Lösen | Betrachten |
Häufig gestellte Fragen (FAQs) zur Memoisierung
1: Ist Auswendiglernen besser als DP?
Memoisierung ist der Top-Down-Ansatz zur Lösung eines Problems mit dynamischer Programmierung. Man nennt es Memoisierung, weil wir ein Memo für die Werte erstellen, die bei der Lösung jedes Problems zurückgegeben werden.
2: Ist das Auswendiglernen dasselbe wie das Zwischenspeichern?
Das Auswendiglernen ist eigentlich eine spezielle Art des Cachings. Der Begriff „Caching“ kann sich im Allgemeinen auf jede Speichertechnik (wie HTTP-Caching) für die zukünftige Verwendung beziehen, Memoizing bezieht sich jedoch insbesondere auf eine Caching-Funktion, die den Wert zurückgibt.
3: Warum erfolgt das Auswendiglernen von oben nach unten?
Der Top-Down-Ansatz zerlegt das große Problem in mehrere Teilprobleme. Wenn das Teilproblem bereits gelöst ist, verwenden Sie die Antwort erneut. Andernfalls lösen Sie das Teilproblem und speichern das Ergebnis in einem Speicher.
4: Verwendet das Auswendiglernen eine Rekursion?
Das Auswendiglernen folgt einem Top-Down-Ansatz zur Lösung des Problems. Es besteht aus Rekursion und Caching. In der Berechnung stellt Rekursion den Prozess des wiederholten Aufrufs von Funktionen dar, während sich Cache auf den Prozess der Speicherung von Zwischenergebnissen bezieht.
5: Sollte ich Tabellierung oder Memoisierung verwenden?
Bei Problemen, bei denen alle Teilprobleme gelöst werden müssen, übertrifft die Tabellierung in der Regel die Memoisierung um einen konstanten Faktor. Dies liegt daran, dass die Tabellierung keinen Rekursionsaufwand hat, was die Zeit zum Auflösen des Rekursionsaufrufstapels aus dem Stapelspeicher verkürzt.
Wann immer ein Teilproblem gelöst werden muss, um das ursprüngliche Problem zu lösen, ist das Auswendiglernen vorzuziehen, da ein Teilproblem träge gelöst wird, d. h. nur die erforderlichen Berechnungen werden ausgeführt.
6: Wo wird das Auswendiglernen verwendet?
Memoisierung ist eine Optimierungstechnik, die zur Beschleunigung von Computerprogrammen verwendet wird, indem die Ergebnisse teurer Funktionsaufrufe zwischengespeichert und zurückgegeben werden, wenn dieselben Eingaben erneut auftreten.
7: Warum heißt es Auswendiglernen?
Der Begriff Memoisierung kommt vom lateinischen Wort „memorandum“ (erinnern), das im amerikanischen Englisch üblicherweise zu „memo“ abgekürzt wird und bedeutet, die Ergebnisse einer Funktion in etwas zum Erinnern umzuwandeln.
8: Wie reduziert das Auswendiglernen die Zeitkomplexität?
Das wiederholte Lösen des gleichen Problems nimmt Zeit in Anspruch und erhöht die Laufzeitkomplexität des Gesamtprogramms. Dieses Problem kann gelöst werden, indem wir einen Cache oder Speicher beibehalten, in dem wir das bereits berechnete Ergebnis des Problems für eine bestimmte Eingabe speichern. Wenn wir also nicht dasselbe Problem erneut berechnen möchten, können wir einfach das im Speicher gespeicherte Ergebnis verwenden und die Zeitkomplexität reduzieren.
9: Was ist der Unterschied zwischen Memoisierung und Caching?
Bei der Memoisierung handelt es sich eigentlich um eine spezielle Art des Cachings, bei der der Rückgabewert einer Funktion basierend auf Eingaben zwischengespeichert wird. Caching ist ein allgemeinerer Begriff. HTTP-Caching ist beispielsweise Caching, aber keine Memoisierung.
10: Warum ist das Tabellieren schneller als das Auswendiglernen?
Die Tabellierung ist in der Regel schneller als die Memoisierung, da sie iterativ ist und die Lösung von Teilproblemen keinen Mehraufwand durch rekursive Aufrufe erfordert.
Memoisierung ist eine Technik, die in der Informatik verwendet wird, um die Ausführung rekursiver oder rechenintensiver Funktionen zu beschleunigen, indem die Ergebnisse von Funktionsaufrufen zwischengespeichert und die zwischengespeicherten Ergebnisse zurückgegeben werden, wenn dieselben Eingaben erneut auftreten.
Die Grundidee der Memoisierung besteht darin, die Ausgabe einer Funktion für einen bestimmten Satz von Eingaben zu speichern und das zwischengespeicherte Ergebnis zurückzugeben, wenn die Funktion erneut mit denselben Eingaben aufgerufen wird. Insbesondere bei Funktionen, die häufig aufgerufen werden oder eine hohe zeitliche Komplexität aufweisen, kann diese Technik Rechenzeit sparen.
Hier ist eine Schritt-für-Schritt-Anleitung zur Implementierung der Memoisierung:
Identifizieren Sie die Funktion, die Sie mithilfe der Memoisierung optimieren möchten. Diese Funktion sollte wiederholte und aufwendige Berechnungen für dieselbe Eingabe durchführen.
Erstellen Sie ein Wörterbuchobjekt, um die zwischengespeicherten Ergebnisse der Funktion zu speichern. Die Schlüssel des Wörterbuchs sollten die Eingabeparameter der Funktion sein und die Werte sollten die berechneten Ergebnisse sein.
Überprüfen Sie zu Beginn der Funktion, ob die Eingabeparameter bereits im Cache-Wörterbuch vorhanden sind. Wenn dies der Fall ist, wird das zwischengespeicherte Ergebnis zurückgegeben.
Wenn die Eingabeparameter nicht im Cache-Wörterbuch enthalten sind, berechnen Sie das Ergebnis und speichern Sie es im Cache-Wörterbuch mit den Eingabeparametern als Schlüssel.
Gibt das berechnete Ergebnis zurück.
Hier ist ein Python-Codebeispiel für die Implementierung der Memoisierung mithilfe eines Wörterbuchs:
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
>Ausgabe
>
Im obigen Code definieren wir eine Funktion namens Fibonacci, die die n-te Zahl in der Fibonacci-Folge berechnet. Wir verwenden ein Wörterbuchobjekt namens Cache, um die Ergebnisse der Funktionsaufrufe zu speichern. Wenn der Eingabeparameter n bereits im Cache-Wörterbuch vorhanden ist, geben wir das zwischengespeicherte Ergebnis zurück. Andernfalls berechnen wir das Ergebnis mithilfe rekursiver Aufrufe der Fibonacci-Funktion und speichern es im Cache-Wörterbuch, bevor wir es zurückgeben.
Memoisierung kann verwendet werden, um die Leistung vieler Funktionen zu optimieren, die wiederholte und teure Berechnungen erfordern. Durch das Zwischenspeichern der Ergebnisse von Funktionsaufrufen können wir unnötige Berechnungen vermeiden und die Ausführung der Funktion beschleunigen.
Abschluss
Memoization ist ein Programmierkonzept und kann auf jede Programmiersprache angewendet werden. Das absolute Ziel ist die Optimierung des Programms. Normalerweise tritt dieses Problem auf, wenn Programme umfangreiche Berechnungen durchführen. Bei dieser Technik werden alle zuvor berechneten Ergebnisse zwischengespeichert, sodass für dasselbe Problem keine Neuberechnung erforderlich ist.
In Verbindung stehende Artikel:
- Auswendiglernen mit Dekoratoren in Python
- JavaScript-Memoisierung
