Ermitteln Sie anhand zweier Zeichenfolgen „X“ und „Y“ die Länge der längsten gemeinsamen Teilzeichenfolge.
Arraylist Java
Beispiele:
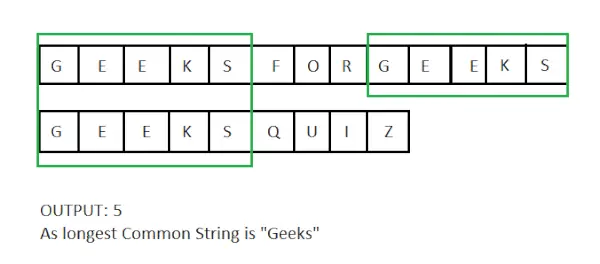
Eingabe: X = techcodeview.com, y = GeeksQuiz
Ausgabe : 5
Erläuterung:
Der längste gemeinsame Teilstring ist Geeks und hat die Länge 5.
Eingabe: X = abcdxyz, y = xyzabcd
Ausgabe : 4
Erläuterung:
Der längste gemeinsame Teilstring ist abcd und hat die Länge 4.Eingabe: X = zxabcdezy, y = yzabcdezx
Ausgabe : 6
Erläuterung:
Der längste gemeinsame Teilstring ist abcdez und hat die Länge 6.
Ansatz:
Seien m und n die Längen der ersten bzw. zweiten Zeichenfolge.
A einfache Lösung besteht darin, nacheinander alle Teilzeichenfolgen der ersten Zeichenfolge zu betrachten und für jede Teilzeichenfolge zu prüfen, ob es sich um eine Teilzeichenfolge in der zweiten Zeichenfolge handelt. Behalten Sie die Teilzeichenfolge mit der maximalen Länge im Auge. Es wird O(m^2) Teilzeichenfolgen geben und wir können in O(n) Zeit herausfinden, ob eine Zeichenkette Teilzeichenfolge einer anderen Zeichenkette ist (siehe Das ). Die Gesamtzeitkomplexität dieser Methode wäre also O(n * m2)
Dynamische Programmierung kann verwendet werden, um den längsten gemeinsamen Teilstring in O(m*n)-Zeit zu finden. Die Idee besteht darin, die Länge des längsten gemeinsamen Suffixes für alle Teilzeichenfolgen beider Zeichenfolgen zu ermitteln und diese Längen in einer Tabelle zu speichern.
Das längste gemeinsame Suffix hat die folgende optimale Unterstruktureigenschaft.
Wenn die letzten Zeichen übereinstimmen, reduzieren wir beide Längen um 1
- LCSuff(X, Y, m, n) = LCSuff(X, Y, m-1, n-1) + 1, wenn X[m-1] = Y[n-1]
Wenn die letzten Zeichen nicht übereinstimmen, ist das Ergebnis 0, d. h.
- LCSuff(X, Y, m, n) = 0 wenn (X[m-1] != Y[n-1])
Nun betrachten wir Suffixe verschiedener Teilzeichenfolgen, die auf unterschiedliche Indizes enden.
Die maximale Länge des Longest Common Suffix ist die längste gemeinsame Teilzeichenfolge.
LCSubStr(X, Y, m, n) = Max(LCSuff(X, Y, i, j)) wobei 1 <= i <= m und 1 <= j <= n
Es folgt die iterative Implementierung der obigen Lösung.
C++
/* Dynamic Programming solution to> >find length of the> >longest common substring */> #include> #include> using> namespace> std;> /* Returns length of longest> >common substring of X[0..m-1]> >and Y[0..n-1] */> int> LCSubStr(>char>* X,>char>* Y,>int> m,>int> n)> {> >// Create a table to store> >// lengths of longest> >// common suffixes of substrings.> >// Note that LCSuff[i][j] contains> >// length of longest common suffix> >// of X[0..i-1] and Y[0..j-1].> >int> LCSuff[m + 1][n + 1];> >int> result = 0;>// To store length of the> >// longest common substring> >/* Following steps build LCSuff[m+1][n+1] in> >bottom up fashion. */> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >// The first row and first column> >// entries have no logical meaning,> >// they are used only for simplicity> >// of program> >if> (i == 0 || j == 0)> >LCSuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;> >result = max(result, LCSuff[i][j]);> >}> >else> >LCSuff[i][j] = 0;> >}> >}> >return> result;> }> // Driver code> int> main()> {> >char> X[] =>'OldSite:techcodeview.com.org'>;> >char> Y[] =>'NewSite:GeeksQuiz.com'>;> >int> m =>strlen>(X);> >int> n =>strlen>(Y);> >cout <<>'Length of Longest Common Substring is '> ><< LCSubStr(X, Y, m, n);> >return> 0;> }> |
>
>
Java
// Java implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> import> java.io.*;> class> GFG {> >/*> >Returns length of longest common substring> >of X[0..m-1] and Y[0..n-1]> >*/> >static> int> LCSubStr(>char> X[],>char> Y[],>int> m,>int> n)> >{> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> >int> LCStuff[][] =>new> int>[m +>1>][n +>1>];> >// To store length of the longest> >// common substring> >int> result =>0>;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (>int> i =>0>; i <= m; i++) {> >for> (>int> j =>0>; j <= n; j++) {> >if> (i ==>0> || j ==>0>)> >LCStuff[i][j] =>0>;> >else> if> (X[i ->1>] == Y[j ->1>]) {> >LCStuff[i][j]> >= LCStuff[i ->1>][j ->1>] +>1>;> >result = Integer.max(result,> >LCStuff[i][j]);> >}> >else> >LCStuff[i][j] =>0>;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> main(String[] args)> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.length();> >int> n = Y.length();> >System.out.println(> >'Length of Longest Common Substring is '> >+ LCSubStr(X.toCharArray(), Y.toCharArray(), m,> >n));> >}> }> // This code is contributed by Sumit Ghosh> |
>
>
Python3
# Python3 implementation of Finding> # Length of Longest Common Substring> # Returns length of longest common> # substring of X[0..m-1] and Y[0..n-1]> def> LCSubStr(X, Y, m, n):> ># Create a table to store lengths of> ># longest common suffixes of substrings.> ># Note that LCSuff[i][j] contains the> ># length of longest common suffix of> ># X[0...i-1] and Y[0...j-1]. The first> ># row and first column entries have no> ># logical meaning, they are used only> ># for simplicity of the program.> ># LCSuff is the table with zero> ># value initially in each cell> >LCSuff>=> [[>0> for> k>in> range>(n>+>1>)]>for> l>in> range>(m>+>1>)]> ># To store the length of> ># longest common substring> >result>=> 0> ># Following steps to build> ># LCSuff[m+1][n+1] in bottom up fashion> >for> i>in> range>(m>+> 1>):> >for> j>in> range>(n>+> 1>):> >if> (i>=>=> 0> or> j>=>=> 0>):> >LCSuff[i][j]>=> 0> >elif> (X[i>->1>]>=>=> Y[j>->1>]):> >LCSuff[i][j]>=> LCSuff[i>->1>][j>->1>]>+> 1> >result>=> max>(result, LCSuff[i][j])> >else>:> >LCSuff[i][j]>=> 0> >return> result> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> print>(>'Length of Longest Common Substring is'>,> >LCSubStr(X, Y, m, n))> # This code is contributed by Soumen Ghosh> |
>
>
C#
// C# implementation of finding length of longest> // Common substring using Dynamic Programming> using> System;> class> GFG {> >// Returns length of longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> LCSubStr(>string> X,>string> Y,>int> m,>int> n)> >{> >// Create a table to store lengths of> >// longest common suffixes of substrings.> >// Note that LCSuff[i][j] contains length> >// of longest common suffix of X[0..i-1]> >// and Y[0..j-1]. The first row and first> >// column entries have no logical meaning,> >// they are used only for simplicity of> >// program> >int>[, ] LCStuff =>new> int>[m + 1, n + 1];> >// To store length of the longest common> >// substring> >int> result = 0;> >// Following steps build LCSuff[m+1][n+1]> >// in bottom up fashion> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >if> (i == 0 || j == 0)> >LCStuff[i, j] = 0;> >else> if> (X[i - 1] == Y[j - 1])> >{> >LCStuff[i, j]> >= LCStuff[i - 1, j - 1] + 1;> >result> >= Math.Max(result, LCStuff[i, j]);> >}> >else> >LCStuff[i, j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> Main()> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >Console.Write(>'Length of Longest Common'> >+>' Substring is '> >+ LCSubStr(X, Y, m, n));> >}> }> // This code is contributed by Sam007.> |
>
>
Javascript
> // JavaScript implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> >/*> >Returns length of longest common> >substring of X[0..m-1] and Y[0..n-1]> >*/> >function> LCSubStr( X, Y , m , n) {> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> > >var> LCStuff => >Array(m + 1).fill().map(()=>Array(n + 1).fill(0));> >// To store length of the longest> >// common substring> >var> result = 0;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (i = 0; i <= m; i++) {> >for> (j = 0; j <= n; j++) {> >if> (i == 0 || j == 0)> >LCStuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;> >result = Math.max(result, LCStuff[i][j]);> >}>else> >LCStuff[i][j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> > >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> >var> m = X.length;> >var> n = Y.length;> >document.write(>'Length of Longest Common Substring is '> +> >LCSubStr(X, Y, m, n));> // This code contributed by Rajput-Ji> > |
>
>
PHP
// Dynamic Programming solution to find // length of the longest common substring // Returns length of longest common // substring of X[0..m-1] and Y[0..n-1] function LCSubStr($X, $Y, $m, $n) { // Create a table to store lengths of // longest common suffixes of substrings. // Notethat LCSuff[i][j] contains length // of longest common suffix of X[0..i-1] // and Y[0..j-1]. The first row and // first column entries have no logical // meaning, they are used only for // simplicity of program $LCSuff = array_fill(0, $m + 1, array_fill(0, $n + 1, NULL)); $result = 0; // To store length of the // longest common substring // Following steps build LCSuff[m+1][n+1] // in bottom up fashion. for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) { if ($i == 0 || $j == 0) $LCSuff[$i][$j] = 0; else if ($X[$i - 1] == $Y[$j - 1]) { $LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1; $result = max($result, $LCSuff[$i][$j]); } else $LCSuff[$i][$j] = 0; } } return $result; } // Driver Code $X = 'OldSite:techcodeview.com.org'; $Y = 'NewSite:GeeksQuiz.com'; $m = strlen($X); $n = strlen($Y); echo 'Length of Longest Common Substring is ' . LCSubStr($X, $Y, $m, $n); // This code is contributed by ita_c ?>> |
>
>Ausgabe
Length of Longest Common Substring is 10>
Zeitkomplexität: O(m*n)
Hilfsraum: O(m*n), da m*n zusätzlicher Platz belegt wurde.
Ein anderer Ansatz: (Raumoptimierter Ansatz).
Im obigen Ansatz verwenden wir nur die letzte Zeile des 2D-Arrays, daher können wir den Platz durch Verwendung optimieren
ein 2D-Array der Dimension 2*(min(n,m)).
Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:
C++
#include> #include> using> namespace> std;> // Function to find the length of the longest LCS> int> LCSubStr(string s, string t,>int> n,>int> m)> {> >// Create DP table> >vectorint>> dp(n + 1, Vektor |
>
>
Java
Bharti Jha
// Java implementation of the above approach> import> java.io.*;> class> GFG> {> > >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(String s,String t,> >int> n,>int> m)> >{> > >// Create DP table> >int> dp[][]=>new> int>[>2>][m+>1>];> >int> res=>0>;> > >for>(>int> i=>1>;i<=n;i++)> >{> >for>(>int> j=>1>;j<=m;j++)> >{> >if>(s.charAt(i->1>)==t.charAt(j->1>))> >{> >dp[i%>2>][j]=dp[(i->1>)%>2>][j->1>]+>1>;> >if>(dp[i%>2>][j]>res)> >res=dp[i%>2>][j];> >}> >else> dp[i%>2>][j]=>0>;> >}> >}> >return> res;> >}> > >// Driver Code> >public> static> void> main (String[] args)> >{> >String X=>'OldSite:techcodeview.com.org'>;> >String Y=>'NewSite:GeeksQuiz.com'>;> > >int> m=X.length();> >int> n=Y.length();> > >// Function call> >System.out.println(LCSubStr(X,Y,m,n));> > >}> }> |
>
>
Python3
Unterstreichen mit CSS
# Python implementation of the above approach> # Function to find the length of the> # longest LCS> def> LCSubStr(s, t, n, m):> > ># Create DP table> >dp>=> [[>0> for> i>in> range>(m>+> 1>)]>for> j>in> range>(>2>)]> >res>=> 0> > >for> i>in> range>(>1>,n>+> 1>):> >for> j>in> range>(>1>,m>+> 1>):> >if>(s[i>-> 1>]>=>=> t[j>-> 1>]):> >dp[i>%> 2>][j]>=> dp[(i>-> 1>)>%> 2>][j>-> 1>]>+> 1> >if>(dp[i>%> 2>][j]>res):> >res>=> dp[i>%> 2>][j]> >else>:> >dp[i>%> 2>][j]>=> 0> >return> res> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> # Function call> print>(LCSubStr(X,Y,m,n))> # This code is contributed by avanitrachhadiya2155> |
>
>
C#
// C# implementation of the above approach> using> System;> public> class> GFG> {> >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(>string> s,>string> t,> >int> n,>int> m)> >{> >// Create DP table> >int>[,] dp =>new> int>[2, m + 1];> >int> res = 0;> >for>(>int> i = 1; i <= n; i++)> >{> >for>(>int> j = 1; j <= m; j++)> >{> >if>(s[i - 1] == t[j - 1])> >{> >dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;> >if>(dp[i % 2, j]>res)> >res = dp[i % 2, j];> >}> >else> dp[i % 2, j] = 0;> >}> >}> >return> res;> >}> >// Driver Code> >static> public> void> Main (){> >string> X =>'OldSite:techcodeview.com.org'>;> >string> Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >// Function call> >Console.WriteLine(LCSubStr(X,Y,m,n));> >}> }> // This code is contributed by rag2127> |
>
>
Javascript
> // JavaScript implementation of the above approach> >// Function to find the length of the> >// longest LCS> >function> LCSubStr(s, t, n, m)> >{> > >// Create DP table> >var> dp = Array(2).fill().map(()=>Array(m+ 1).fill(0));> >var> res = 0;> > >for>(>var> i = 1; i <= n; i++)> >{> >for>(>var> j = 1; j <= m; j++)> >{> >if>(s.charAt(i - 1) == t.charAt(j - 1))> >{> >dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;> >if>(dp[i % 2][j]>res)> >res = dp[i % 2][j];> >}> >else> dp[i % 2][j] = 0;> >}> >}> >return> res;> >}> > >// Driver Code> >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> > >var> m = X.length;> >var> n = Y.length;> > >// Function call> >document.write(LCSubStr(X, Y, m, n));> // This code is contributed by shivanisinghss2110> > |
>
>Ausgabe
10>
Zeitkomplexität: O(n*m)
Hilfsraum: O(min(m,n))
Ein anderer Ansatz: (Verwendung von Rekursion)
Hier ist die rekursive Lösung des obigen Ansatzes.
C++
// C++ program using to find length of the> // longest common substring recursion> #include> using> namespace> std;> string X, Y;> // Returns length of function f> // or longest common substring> // of X[0..m-1] and Y[0..n-1]> int> lcs(>int> i,>int> j,>int> count)> {> >if> (i == 0 || j == 0)> >return> count;> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = max(count,> >max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> }> // Driver code> int> main()> {> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.size();> >m = Y.size();> >cout << lcs(n, m, 0);> >return> 0;> }> |
>
>
Java
// Java program using to find length of the> // longest common substring recursion> import> java.io.*;> class> GFG {> >static> String X, Y;> >// Returns length of function> >// for longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i ==>0> || j ==>0>)> >{> >return> count;> >}> >if> (X.charAt(i ->1>)> >== Y.charAt(j ->1>))> >{> >count = lcs(i ->1>, j ->1>, count +>1>);> >}> >count = Math.max(count,> >Math.max(lcs(i, j ->1>,>0>),> >lcs(i ->1>, j,>0>)));> >return> count;> >}> > >// Driver code> >public> static> void> main(String[] args)> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.length();> >m = Y.length();> >System.out.println(lcs(n, m,>0>));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Python3
# Python3 program using to find length of> # the longest common substring recursion> # Returns length of function for longest> # common substring of X[0..m-1] and Y[0..n-1]> def> lcs(i, j, count):> >if> (i>=>=> 0> or> j>=>=> 0>):> >return> count> >if> (X[i>-> 1>]>=>=> Y[j>-> 1>]):> >count>=> lcs(i>-> 1>, j>-> 1>, count>+> 1>)> >count>=> max>(count,>max>(lcs(i, j>-> 1>,>0>),> >lcs(i>-> 1>, j,>0>)))> >return> count> # Driver code> if> __name__>=>=> '__main__'>:> >X>=> 'abcdxyz'> >Y>=> 'xyzabcd'> >n>=> len>(X)> >m>=> len>(Y)> >print>(lcs(n, m,>0>))> # This code is contributed by Ryuga> |
>
>
C#
// C# program using to find length> // of the longest common substring> // recursion> using> System;> class> GFG {> >static> String X, Y;> >// Returns length of function for> >// longest common substring of> >// X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i == 0 || j == 0) {> >return> count;> >}> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> >// Driver code> >public> static> void> Main()> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.Length;> >m = Y.Length;> >Console.Write(lcs(n, m, 0));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Javascript
> >// Javascript program using to find length of the> >// longest common substring recursion> >let X, Y;> > >// Returns length of function f> >// or longest common substring> >// of X[0..m-1] and Y[0..n-1]> >function> lcs(i, j, count)> >{> > >if> (i == 0 || j == 0)> >return> count;> > >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.max(count,> >Math.max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> > >let n, m;> > >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> > >n = X.length;> >m = Y.length;> > >document.write(lcs(n, m, 0));> > >// This code is contributed by divyeshrabadiya07.> > |
q3 Monate
>
>
PHP
// PHP program using to find length of the // longest common substring recursion // Returns length of function for // longest common substring of // X[0..m-1] and Y[0..n-1] function lcs($i, $j, $count, &$X, &$Y) { if ($i == 0 || $j == 0) return $count; if ($X[$i - 1] == $Y[$j - 1]) { $count = lcs($i - 1, $j - 1, $count + 1, $X, $Y); } $count = max($count, lcs($i, $j - 1, 0, $X, $Y), lcs($i - 1, $j, 0, $X, $Y)); return $count; } // Driver code $X = 'abcdxyz'; $Y = 'xyzabcd'; $n = strlen($X); $m = strlen($Y); echo lcs($n, $m, 0, $X, $Y); // This code is contributed // by rathbhupendra ?>> |
>
>Ausgabe
4>
Zeitkomplexität : O(2^max(m,n)) da die Funktion zwei rekursive Aufrufe ausführt – lcs(i, j-1, 0) und lcs(i-1, j, 0), wenn Zeichen bei X[i-1] != Y[j-1]. Im schlimmsten Fall ergibt sich also eine Zeitkomplexität von 2^N, wobei N = max(m, n), m und n die Länge der X- und Y-Zeichenfolge ist.
Hilfsraum: O(1): da der Funktionsaufruf keinen zusätzlichen Speicherplatz beansprucht (die Funktion verwendet lediglich einen rekursiven Aufrufstapel, den wir im Allgemeinen nicht im Hilfsbereich berücksichtigen).
