 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; }Ermitteln Sie anhand eines Binärbaums die Länge des längsten Pfads, der aus Knoten mit aufeinanderfolgenden Werten in aufsteigender Reihenfolge besteht. Jeder Knoten wird als Pfad der Länge 1 betrachtet.
Beispiele:
In below diagram binary tree with longest consecutive path(LCP) are shown :
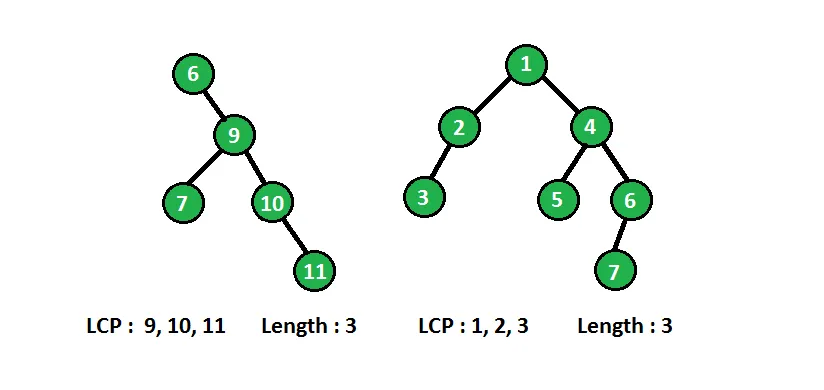
Wir können das obige Problem rekursiv lösen. An jedem Knoten benötigen wir Informationen über seinen übergeordneten Knoten. Wenn der aktuelle Knoten einen um eins höheren Wert als sein übergeordneter Knoten hat, erstellt er einen fortlaufenden Pfad. An jedem Knoten vergleichen wir den Wert des Knotens mit seinem übergeordneten Wert und aktualisieren den längsten fortlaufenden Pfad entsprechend.
Um den Wert des übergeordneten Knotens zu erhalten, übergeben wir (node_value + 1) als Argument an die rekursive Methode und vergleichen den Knotenwert mit diesem Argumentwert, wenn dies erfüllt ist, aktualisieren Sie die aktuelle Länge des aufeinanderfolgenden Pfads, andernfalls initialisieren Sie die aktuelle Pfadlänge um 1 neu.
r in der C-Programmierung
Zum besseren Verständnis sehen Sie sich bitte den folgenden Code an:
C++// C/C++ program to find longest consecutive // sequence in binary tree #include
// Java program to find longest consecutive // sequence in binary tree class Node { int data; Node left right; Node(int item) { data = item; left = right = null; } } class Result { int res = 0; } class BinaryTree { Node root; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive(Node root) { if (root == null) return 0; Result res = new Result(); // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res.res; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil(Node root int curlength int expected Result res) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res.res = Math.max(res.res curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = new Node(6); tree.root.right = new Node(9); tree.root.right.left = new Node(7); tree.root.right.right = new Node(10); tree.root.right.right.right = new Node(11); System.out.println(tree.longestConsecutive(tree.root)); } } // This code is contributed by shubham96301
# Python3 program to find longest consecutive # sequence in binary tree # A utility class to create a node class newNode: def __init__(self data): self.data = data self.left = self.right = None # Utility method to return length of # longest consecutive sequence of tree def longestConsecutiveUtil(root curLength expected res): if (root == None): return # if root data has one more than its # parent then increase current length if (root.data == expected): curLength += 1 else: curLength = 1 # update the maximum by current length res[0] = max(res[0] curLength) # recursively call left and right subtree # with expected value 1 more than root data longestConsecutiveUtil(root.left curLength root.data + 1 res) longestConsecutiveUtil(root.right curLength root.data + 1 res) # method returns length of longest consecutive # sequence rooted at node root def longestConsecutive(root): if (root == None): return 0 res = [0] # call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res) return res[0] # Driver Code if __name__ == '__main__': root = newNode(6) root.right = newNode(9) root.right.left = newNode(7) root.right.right = newNode(10) root.right.right.right = newNode(11) print(longestConsecutive(root)) # This code is contributed by PranchalK
// C# program to find longest consecutive // sequence in binary tree using System; class Node { public int data; public Node left right; public Node(int item) { data = item; left = right = null; } } class Result { public int res = 0; } class GFG { Node root; // method returns length of longest consecutive // sequence rooted at node root int longestConsecutive(Node root) { if (root == null) return 0; Result res = new Result(); // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res.res; } // Utility method to return length of longest // consecutive sequence of tree private void longestConsecutiveUtil(Node root int curlength int expected Result res) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res.res = Math.Max(res.res curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code public static void Main(String []args) { GFG tree = new GFG(); tree.root = new Node(6); tree.root.right = new Node(9); tree.root.right.left = new Node(7); tree.root.right.right = new Node(10); tree.root.right.right.right = new Node(11); Console.WriteLine(tree.longestConsecutive(tree.root)); } } // This code is contributed by 29AjayKumar
<script> // JavaScript program to find longest consecutive // sequence in binary tree class Node { constructor(item) { this.data=item; this.left = this.right = null; } } let res = 0; let root; function longestConsecutive(root) { if (root == null) return 0; res=[0]; // call utility method with current length 0 longestConsecutiveUtil(root 0 root.data res); return res[0]; } // Utility method to return length of longest // consecutive sequence of tree function longestConsecutiveUtil(rootcurlength expectedres) { if (root == null) return; // if root data has one more than its parent // then increase current length if (root.data == expected) curlength++; else curlength = 1; // update the maximum by current length res[0] = Math.max(res[0] curlength); // recursively call left and right subtree with // expected value 1 more than root data longestConsecutiveUtil(root.left curlength root.data + 1 res); longestConsecutiveUtil(root.right curlength root.data + 1 res); } // Driver code root = new Node(6); root.right = new Node(9); root.right.left = new Node(7); root.right.right = new Node(10); root.right.right.right = new Node(11); document.write(longestConsecutive(root)); // This code is contributed by rag2127 </script>
Ausgabe
3
Zeitkomplexität: O(N), wobei N die Anzahl der Knoten in einem bestimmten Binärbaum ist.
Hilfsraum: O(log(N))
Wird auch unter folgendem Link besprochen:
Maximale aufeinanderfolgende zunehmende Pfadlänge im Binärbaum
