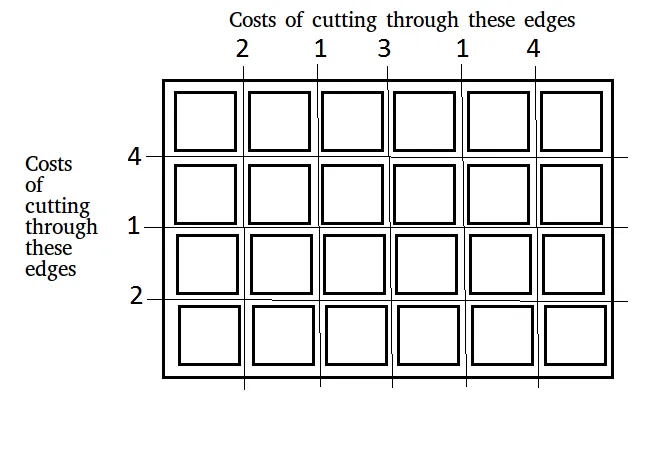
Gegeben sei eine Tafel mit Maßen n × m das muss in n × m Quadrate zerschnitten werden. Die Kosten für einen Schnitt entlang einer horizontalen oder vertikalen Kante werden in zwei Gruppen angegeben:

• X[] : Kostensenkung entlang der vertikalen Kanten (in Längsrichtung).
• Und[] : Kostensenkung entlang der horizontalen Kanten (in der Breite).

Ermitteln Sie die minimalen Gesamtkosten, die erforderlich sind, um das Brett optimal in Quadrate zu schneiden.

Beispiele: 

Eingang: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Ausgabe: 42
Erläuterung:

Zunächst nein. der horizontalen Segmente = 1 & Nr. der vertikalen Segmente = 1.
Der optimale Weg, in Quadrate zu schneiden, ist:
Wählen Sie 4 (von x) -> Kosten für vertikalen Schnitt = 4 × horizontale Segmente = 4
 Jetzt horizontale Segmente = 1 vertikale Segmente = 2.
Wählen Sie 4 (von y) -> Kosten für horizontalen Schnitt = 4 × vertikale Segmente = 8
 Jetzt horizontale Segmente = 2 vertikale Segmente = 2.
Wählen Sie 3 (von x) -> Kosten für vertikalen Schnitt = 3 × horizontale Segmente = 6
 Jetzt horizontale Segmente = 2 vertikale Segmente = 3.
Wählen Sie 2 (von x) -> Kosten für vertikalen Schnitt = 2 × horizontale Segmente = 4
 Jetzt horizontale Segmente = 2 vertikale Segmente = 4.
Wählen Sie 2 (von y) -> Kosten für horizontalen Schnitt = 2 × vertikale Segmente = 8
 Jetzt horizontale Segmente = 3 vertikale Segmente = 4.
Wählen Sie 1 (von x) -> Kosten für vertikalen Schnitt = 1 × horizontale Segmente = 3
Jetzt horizontale Segmente = 3 vertikale Segmente = 5.
Wählen Sie 1 (von x) -> Kosten für vertikalen Schnitt = 1 × horizontale Segmente = 3
Jetzt horizontale Segmente = 3 vertikale Segmente = 6.
Wählen Sie 1 (von y) -> Kosten für horizontalen Schnitt = 1 × vertikale Segmente = 6
Jetzt horizontale Segmente = 4 vertikale Segmente = 6.
Die Gesamtkosten betragen also 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Eingang: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Ausgabe: 15
Erläuterung:
Zunächst nein. der horizontalen Segmente = 1 & Nr. der vertikalen Segmente = 1.
Der optimale Weg, in Quadrate zu schneiden, ist:
Wählen Sie 1 (von y) -> Kosten für horizontalen Schnitt = 1 × vertikale Segmente = 1
Jetzt horizontale Segmente = 2 vertikale Segmente = 1.
Wählen Sie 1 (von y) -> Kosten für horizontalen Schnitt = 1 × vertikale Segmente = 1
Jetzt horizontale Segmente = 3 vertikale Segmente = 1.
Wählen Sie 1 (von y) -> Kosten für horizontalen Schnitt = 1 × vertikale Segmente = 1
Jetzt horizontale Segmente = 4 vertikale Segmente = 1.
Wählen Sie 1 (von x) -> Kosten für vertikalen Schnitt = 1 × horizontale Segmente = 4
Jetzt horizontale Segmente = 4 vertikale Segmente = 2.
Wählen Sie 1 (von x) -> Kosten für vertikalen Schnitt = 1 × horizontale Segmente = 4
Jetzt horizontale Segmente = 4 vertikale Segmente = 3.
Wählen Sie 1 (von x) -> Kosten für vertikalen Schnitt = 1 × horizontale Segmente = 4
Jetzt horizontale Segmente = 4 vertikale Segmente = 4
Die Gesamtkosten betragen also 1 + 1 + 1 + 4 + 4 + 4 = 15.

Inhaltsverzeichnis

• [Naiver Ansatz] Probieren Sie alle Permutationen aus – O((n+m)!×(n+m)) Zeit und O(n+m) Raum
• [Erwarteter Ansatz] Verwendung der Greedy-Technik – O( n (log n)+m (log m)) Zeit und O(1) Raum

[Naiver Ansatz] Probieren Sie alle Permutationen aus – O((n+m)!×(n+m)) Zeit und O(n+m) Raum

Die Idee besteht darin, alle möglichen Permutationen der gegebenen Schnitte zu generieren und dann die Kosten für jede Permutation zu berechnen. Geben Sie schließlich die Mindestkosten unter ihnen zurück.

Notiz: Dieser Ansatz ist für größere Eingaben nicht durchführbar, da die Anzahl der Permutationen faktoriell mit (m+n-2)! wächst.
Für jede Permutation müssen wir die Kosten in O(m+n) Zeit berechnen. Daher beträgt die Gesamtzeitkomplexität O((m+n−2)!×(m+n)).

[Erwarteter Ansatz] Verwendung der Greedy-Technik – O( n (log n)+m (log m)) Zeit und O(1) Raum

Die Idee besteht darin, zuerst die teuersten Schnitte mit einem zu machen gieriger Ansatz . Die Beobachtung ist, dass die Wahl der höchsten Kostensenkung bei jedem Schritt zukünftige Kosten senkt, da mehrere Teile gleichzeitig betroffen sind. Wir sortieren die vertikalen (x) und horizontalen (y) Kosteneinsparungen in absteigender Reihenfolge und wählen dann iterativ die größere aus, um die Kosteneinsparungen zu maximieren. Die restlichen Schnitte werden separat verarbeitet, um eine optimale Aufteilung aller Abschnitte zu gewährleisten.

Was passiert, wenn wir einen Schnitt machen?

• Horizontaler Schnitt → Sie schneiden über die Breite, sodass die Anzahl der horizontalen Streifen zunimmt (hCount++). Die Kosten werden jedoch mit vCount (der Anzahl der vertikalen Streifen) multipliziert, da der horizontale Schnitt durch alle vertikalen Segmente gehen muss.
• Vertikaler Schnitt → Sie schneiden über die Höhe, sodass die Anzahl der vertikalen Streifen zunimmt (vCount++). Die Kosten werden jedoch mit hCount (der Anzahl der horizontalen Streifen) multipliziert, da der vertikale Schnitt durch alle horizontalen Segmente gehen muss.

Schritte zur Lösung des Problems:

• Sortieren Sie sowohl X- als auch Y-Arrays in absteigender Reihenfolge.
• Verwenden Sie zwei Zeiger, einen für x und einen für y, beginnend beim größten Wert und in Richtung kleinerer Werte.
• Behalten Sie hCount und vCount bei, um zu verfolgen, wie viele Segmente jeder Schnitt betrifft, und aktualisieren Sie sie entsprechend.
• Während sowohl
• Wenn x verbleibende Schnitte vorhanden sind, verarbeiten Sie diese mit dem hCount-Multiplikator. Verarbeiten Sie die verbleibenden Y-Schnitte auf ähnliche Weise mit vCount.
• Berechnen Sie die Gesamtkosten für jeden Schritt anhand der Formel: Kosten senken * Anzahl der betroffenen Teile, um minimale Kosten zu gewährleisten.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42