Bei einem 3D-Array arr[l][m][n] besteht die Aufgabe darin, die minimale Pfadsumme von der ersten Zelle des Arrays bis zur letzten Zelle des Arrays zu ermitteln. Wir können nur zum benachbarten Element traversieren, d. h. von einer gegebenen Zelle (i j k) können die Zellen (i+1 j k), (i j+1 k) und (i j k+1) traversiert werden. Diagonales Traversieren ist nicht erlaubt. Wir können davon ausgehen, dass alle Kosten positive ganze Zahlen sind.
Beispiele:
Input : arr[][][]= { {{1 2} {3 4}} {{4 8} {5 2}} }; Output : 9 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] Input : { { {1 2} {4 3}} { {3 4} {2 1}} }; Output : 7 Explanation : arr[0][0][0] + arr[0][0][1] + arr[0][1][1] + arr[1][1][1] Betrachten wir ein 3D-Array arr[2][2][2], dargestellt durch einen Quader mit folgenden Werten:
arr[][][] = {{{1 2} {3 4}} { {4 8} {5 2}}}; Result = 9 is calculated as: 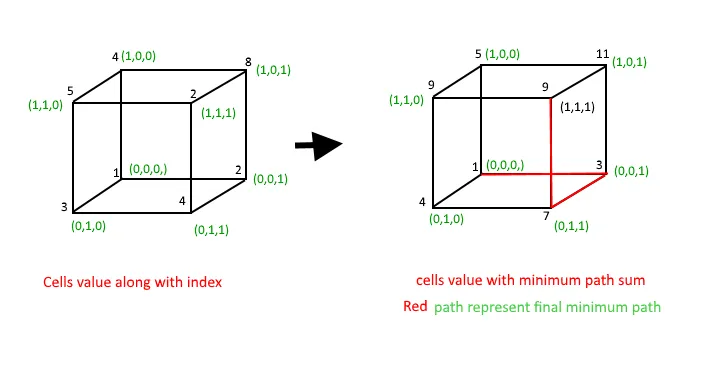
Dieses Problem ähnelt Minimaler Kostenpfad. und kann mit dynamischer Programmierung gelöst werden.
// Array for storing result int tSum[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0] tSum[i][j-1][0] INT_MAX) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k] tSum[i][0][k-1] INT_MAX) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1] tSum[0][j-1][k] INT_MAX) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k] tSum[i][j-1][k] tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1];C++
// C++ program for Min path sum of 3D-array #include
// Java program for Min path sum of 3D-array import java.io.*; class GFG { static int l =3; static int m =3; static int n =3; // A utility function that returns minimum // of 3 integers static int min(int x int y int z) { return (x < y)? ((x < z)? x : z) : ((y < z)? y : z); } // function to calculate MIN path sum of 3D array static int minPathSum(int arr[][][]) { int i j k; int tSum[][][] =new int[l][m][n]; tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i-1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j-1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k-1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i-1][j][0] tSum[i][j-1][0] Integer.MAX_VALUE) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i-1][0][k] tSum[i][0][k-1] Integer.MAX_VALUE) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k-1] tSum[0][j-1][k] Integer.MAX_VALUE) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i-1][j][k] tSum[i][j-1][k] tSum[i][j][k-1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver program public static void main (String[] args) { int arr[][][] = { { {1 2 4} {3 4 5} {5 2 1}} { {4 8 3} {5 2 1} {3 4 2}} { {2 4 1} {3 1 4} {6 3 8}} }; System.out.println ( minPathSum(arr)); } } // This code is contributed by vt_m
# Python3 program for Min # path sum of 3D-array l = 3 m = 3 n = 3 # A utility function # that returns minimum # of 3 integers def Min(x y z): return min(min(xy)z) # function to calculate MIN # path sum of 3D array def minPathSum(arr): tSum = [[[0 for k in range(n)]for j in range(m)] for i in range(l)] tSum[0][0][0] = arr[0][0][0] # Initialize first # row of tSum array for i in range(1l): tSum[i][0][0] = tSum[i - 1][0][0] + arr[i][0][0] # Initialize first column # of tSum array for j in range(1m): tSum[0][j][0] = tSum[0][j - 1][0] + arr[0][j][0] # Initialize first # width of tSum array for k in range(1n): tSum[0][0][k] = tSum[0][0][k - 1] + arr[0][0][k] # Initialize first # row- First column of # tSum array for i in range(1l): for j in range(1m): tSum[i][j][0] = Min(tSum[i - 1][j][0]tSum[i][j - 1][0]1000000000) + arr[i][j][0]; # Initialize first # row- First width of # tSum array for i in range(1l): for k in range(1n): tSum[i][0][k] = Min(tSum[i - 1][0][k]tSum[i][0][k - 1]1000000000) + arr[i][0][k] # Initialize first # width- First column of # tSum array for k in range(1n): for j in range(1m): tSum[0][j][k] = Min(tSum[0][j][k - 1]tSum[0][j - 1][k]1000000000) + arr[0][j][k] # Construct rest of # the tSum array for i in range(1l): for j in range(1m): for k in range(1n): tSum[i][j][k] = Min(tSum[i - 1][j][k]tSum[i][j - 1][k]tSum[i][j][k - 1]) + arr[i][j][k] return tSum[l-1][m-1][n-1] # Driver Code arr = [[[1 2 4] [3 4 5] [5 2 1]] [[4 8 3] [5 2 1] [3 4 2]] [[2 4 1] [3 1 4] [6 3 8]]] print(minPathSum(arr)) # This code is contributed by shinjanpatra
// C# program for Min // path sum of 3D-array using System; class GFG { static int l = 3; static int m = 3; static int n = 3; // A utility function // that returns minimum // of 3 integers static int min(int x int y int z) { return (x < y) ? ((x < z) ? x : z) : ((y < z) ? y : z); } // function to calculate MIN // path sum of 3D array static int minPathSum(int []arr) { int i j k; int [ ]tSum = new int[l m n]; tSum[0 0 0] = arr[0 0 0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i 0 0] = tSum[i - 1 0 0] + arr[i 0 0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0 j 0] = tSum[0 j - 1 0] + arr[0 j 0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0 0 k] = tSum[0 0 k - 1] + arr[0 0 k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i j 0] = min(tSum[i - 1 j 0] tSum[i j - 1 0] int.MaxValue) + arr[i j 0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i 0 k] = min(tSum[i - 1 0 k] tSum[i 0 k - 1] int.MaxValue) + arr[i 0 k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0 j k] = min(tSum[0 j k - 1] tSum[0 j - 1 k] int.MaxValue) + arr[0 j k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i j k] = min(tSum[i - 1 j k] tSum[i j - 1 k] tSum[i j k - 1]) + arr[i j k]; return tSum[l-1m-1n-1]; } // Driver Code static public void Main () { int [ ]arr= {{{1 2 4} {3 4 5} {5 2 1}} {{4 8 3} {5 2 1} {3 4 2}} {{2 4 1} {3 1 4} {6 3 8}}}; Console.WriteLine(minPathSum(arr)); } } // This code is contributed by ajit
<script> // Javascript program for Min // path sum of 3D-array var l = 3; var m = 3; var n = 3; // A utility function // that returns minimum // of 3 integers function min(x y z) { return (x < y) ? ((x < z) ? x : z) : ((y < z) ? y : z); } // function to calculate MIN // path sum of 3D array function minPathSum(arr) { var i j k; var tSum = Array(l); for(var i = 0; i<l;i++) { tSum[i] = Array.from(Array(m) ()=>Array(n)); } tSum[0][0][0] = arr[0][0][0]; /* Initialize first row of tSum array */ for (i = 1; i < l; i++) tSum[i][0][0] = tSum[i - 1][0][0] + arr[i][0][0]; /* Initialize first column of tSum array */ for (j = 1; j < m; j++) tSum[0][j][0] = tSum[0][j - 1][0] + arr[0][j][0]; /* Initialize first width of tSum array */ for (k = 1; k < n; k++) tSum[0][0][k] = tSum[0][0][k - 1] + arr[0][0][k]; /* Initialize first row- First column of tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) tSum[i][j][0] = min(tSum[i - 1][j][0] tSum[i][j - 1][0] 1000000000) + arr[i][j][0]; /* Initialize first row- First width of tSum array */ for (i = 1; i < l; i++) for (k = 1; k < n; k++) tSum[i][0][k] = min(tSum[i - 1][0][k] tSum[i][0][k - 1] 1000000000) + arr[i][0][k]; /* Initialize first width- First column of tSum array */ for (k = 1; k < n; k++) for (j = 1; j < m; j++) tSum[0][j][k] = min(tSum[0][j][k - 1] tSum[0][j - 1][k] 1000000000) + arr[0][j][k]; /* Construct rest of the tSum array */ for (i = 1; i < l; i++) for (j = 1; j < m; j++) for (k = 1; k < n; k++) tSum[i][j][k] = min(tSum[i - 1][j][k] tSum[i][j - 1][k] tSum[i][j][k - 1]) + arr[i][j][k]; return tSum[l-1][m-1][n-1]; } // Driver Code var arr= [[[1 2 4] [3 4 5] [5 2 1]] [[4 8 3] [5 2 1] [3 4 2]] [[2 4 1] [3 1 4] [6 3 8]]]; document.write(minPathSum(arr)); </script>
Ausgabe:
20
Zeitkomplexität: O(l*m*n)
Hilfsraum: O(l*m*n)
