Die Normalkraft ist definiert als die Kraft, die eine beliebige Oberfläche auf ein anderes Objekt ausübt. Wenn ein Körper ruht, ist die auf ihn ausgeübte Nettokraft gleich Null. Auf zwei Flächen, die nicht miteinander verbunden sind, kann keine Normalkraft ausgeübt werden. Sie kann als Komponente der Kraft interpretiert werden, die senkrecht zu einer beliebigen Kontaktfläche steht. Sie bestimmt, wie viel Kraft der Körper auf den Boden überträgt. Die Normalkraft ist nur dann gleich dem Gewicht des Objekts, wenn die Geschwindigkeitsänderungsrate des Objekts negativ ist, was bedeutet, dass es langsamer wird.
Formel
Der Wert der Normalkraft hängt davon ab, wo das Objekt im Verhältnis zum anderen Objekt platziert ist. Wenn ein Objekt fallen soll, bestimmt die Position, in der das Objekt auf den Boden fällt, den Wert der Normalkraft. Die Normalkraft wird mit dem Symbol F bezeichnetN. Seine Maßeinheit ist Newton (N) und die Dimensionsformel wird durch [M1L1T-2].
Wenn ein Körper auf einer flachen Kraft ruht, entspricht die Normalkraft dem Wert der Schwerkraft, also mg.
F N = mg
Wo,
FNist die Normalkraft,
m ist die Masse des ruhenden Objekts,
g ist die Erdbeschleunigung.
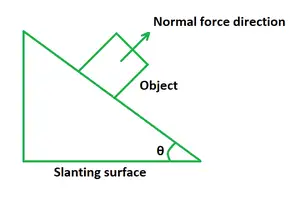
Wenn ein Körper in einem bestimmten Winkel von einer schrägen Oberfläche nach unten rutscht, ist der Wert der Normalkraft das Gravitationsgewicht, zu dem eine zusätzliche Kraft von F sin θ hinzukommt. In diesem Fall ist die Normalkraft größer als das Gewicht des Gegenstandes.
F N = mg + F sin θ
Wo,
FNist die Normalkraft,
m ist die Masse des gleitenden Objekts,
g ist die Erdbeschleunigung,
θ ist der Neigungswinkel.
Wenn die Kraft auf einen Körper in Aufwärtsrichtung wirkt, ist der Wert der Normalkraft das Gravitationsgewicht, vermindert um eine Kraft von F sin θ. In diesem Fall ist die Nettonormalkraft kleiner als das Gewicht des Objekts.
F N = mg – F sin θ
Wo,
Python-Druck auf 2 DezimalstellenFNist die Normalkraft,
m ist die Masse des gleitenden Objekts,
g ist die Erdbeschleunigung,
θ ist der Neigungswinkel.
Wird ein Körper auf eine schiefe Ebene gelegt, so wirkt die Normalkraft FNentspricht dem Produkt aus Schwerkraft und Kosinus des Neigungswinkels.
F N = mg cos θ
Wo,
FNist die Normalkraft,
m ist die Masse des gleitenden Objekts,
g ist die Erdbeschleunigung,
θ ist der Neigungswinkel.
Beispielprobleme
Aufgabe 1. Ein Gegenstand mit einer Masse von 2 kg ruht auf einem Tisch. Berechnen Sie die darauf wirkende Normalkraft.
Lösung:
Wir haben,
m = 2
g = 9,8
Mit der Formel erhalten wir
FN= mg
= 2 (9,8)
= 19,6 N
Aufgabe 2. Ein Gegenstand ruht mit einer Kraft von 39,2 N auf einem Tisch. Berechnen Sie die Normalkraft, die auf ihn ausgeübt wird.
Lösung:
Wir haben,
F = 39,2
g = 9,8
Mit der Formel erhalten wir
FN= mg
=> m = F/g
=> m = 39,2/9,8
=> m = 4 kg
Aufgabe 3. Ein Gegenstand mit einer Masse von 10 kg rutscht mit einer Kraft von 200 N von einer schrägen Oberfläche in einem Winkel von 30° nach unten. Berechnen Sie die darauf wirkende Normalkraft.
Lösung:
Wir haben,
Linkedlist JavaF = 200
m = 10
g = 9,8
θ = 30°
Mit der Formel erhalten wir
FN= mg + F sin θ
= 10 (9,8) + 200 sin 30°
= 98 + 200 (1/2)
= 98 + 100
= 198 N
Aufgabe 4. Ein Objekt mit einer Masse von 20 kg rutscht mit einer Kraft von 400 N von einer schrägen Oberfläche in einem Winkel von 30° nach unten. Berechnen Sie die darauf wirkende Normalkraft.
Lösung:
Wir haben,
F = 400
m = 20
g = 9,8
θ = 30°
Mit der Formel erhalten wir
FN= mg + F sin θ
= 20 (9,8) + 400 ohne 30°
= 196 + 400 (1/2)
= 196 + 200
= 396 N
Aufgabe 5. Ein Gegenstand mit einer Masse von 15 kg wird in einem Winkel von 30° auf eine schräge Fläche gestellt. Berechnen Sie die Normalkraft, die darauf ausgeübt wird, wenn die Kraft nach oben wirkt und einen Wert von 100 N hat.
Lösung:
Wir haben,
F = 100
m = 15
g = 9,8
θ = 30°
Mit der Formel erhalten wir
FN= mg – F sin θ
= 15 (9,8) – 100 ohne 30°
= 147 – 100 (1/2)
= 147 – 50
= 97 N
Aufgabe 6. Ein Gegenstand mit einer Masse von 5 kg wird in einem Winkel von 60° auf eine schräge Fläche gestellt. Berechnen Sie die Normalkraft, die an jedem Punkt darauf ausgeübt wird.
Lösung:
Wir haben,
m = 5
g = 9,8
Wie viele Städte gibt es in uns?θ = 60°
Mit der Formel erhalten wir
FN= mg cos θ
= 5 (9,8) (cos 60°)
= 49/2
= 24,5 N
Aufgabe 7. Ein Gegenstand wird in einem Winkel von 60° auf eine schräge Fläche gestellt. Berechnen Sie seine Masse, wenn die auf ihn ausgeübte Normalkraft 400 N beträgt.
Lösung:
Wir haben,
FN= 400,
θ = 60°
Mit der Formel erhalten wir
FN= mg cos θ
m = F/(g cos θ)
= 400/ (9,8 × cos 60°)
= 400/4,9
= 81,63 N
