| Rundfunk: | Der Begriff Broadcasting beschreibt, wie NumPy Arrays mit unterschiedlichen Formen bei arithmetischen Operationen behandelt. Vorbehaltlich bestimmter Einschränkungen wird das kleinere Array über das größere Array „gesendet“, sodass diese kompatible Formen haben. Broadcasting bietet eine Möglichkeit, Array-Operationen zu vektorisieren, sodass Schleifen in C statt in Python erfolgen. Dies geschieht, ohne dass unnötige Datenkopien erstellt werden, und führt in der Regel zu effizienten Algorithmusimplementierungen. Es gibt auch Fälle, in denen Broadcasting eine schlechte Idee ist, weil es zu einer ineffizienten Speichernutzung führt, die die Berechnung verlangsamt. NumPy-Operationen werden normalerweise Element für Element ausgeführt, was erfordert, dass zwei Arrays genau die gleiche Form haben. Die Broadcasting-Regel von Numpy lockert diese Einschränkung, wenn die Formen der Arrays bestimmte Einschränkungen erfüllen. Die Rundfunkregel: Um die Größe der nachgestellten Achsen für beide Arrays in einem Vorgang zu übertragen, müssen sie entweder gleich groß sein oder eine von ihnen muss gleich groß sein eins . Let us see some examples: A(2-D array): 4 x 3 B(1-D array): 3 Result : 4 x 3
A(4-D array): 7 x 1 x 6 x 1 B(3-D array): 3 x 1 x 5 Result : 7 x 3 x 6 x 5
But this would be a mismatch: A: 4 x 3 B: 4
The simplest broadcasting example occurs when an array and a scalar value are combined in an operation. Consider the example given below: Python import numpy as np a = np.array([1.0 2.0 3.0]) # Example 1 b = 2.0 print(a * b) # Example 2 c = [2.0 2.0 2.0] print(a * c)
[ 2. 4. 6.] [ 2. 4. 6.]
We can think of the scalar b being stretched during the arithmetic operation into an array with the same shape as a. The new elements in b as shown in above figure are simply copies of the original scalar. Although the stretching analogy is only conceptual. Numpy is smart enough to use the original scalar value without actually making copies so that broadcasting operations are as memory and computationally efficient as possible. Because Example 1 moves less memory (b is a scalar not an array) around during the multiplication it is about 10% faster than Example 2 using the standard numpy on Windows 2000 with one million element arrays! The figure below makes the concept more clear: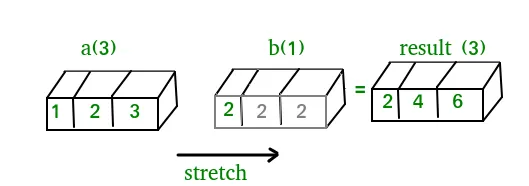 
In above example the scalar b is stretched to become an array of with the same shape as a so the shapes are compatible for element-by-element multiplication. Now let us see an example where both arrays get stretched. Python import numpy as np a = np.array([0.0 10.0 20.0 30.0]) b = np.array([0.0 1.0 2.0]) print(a[: np.newaxis] + b)
[[ 0. 1. 2.] [ 10. 11. 12.] [ 20. 21. 22.] [ 30. 31. 32.]]
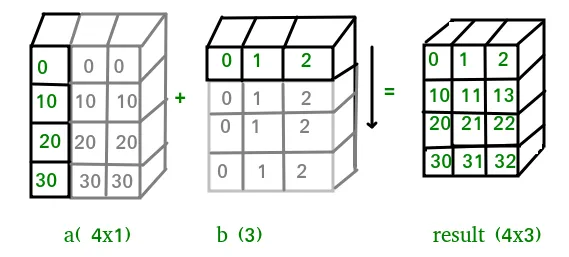In manchen Fällen werden beim Broadcasting beide Arrays gedehnt, um ein Ausgabearray zu bilden, das größer ist als jedes der ursprünglichen Arrays.
| Lineare Algebra in NumPy: | Das Modul „Lineare Algebra“ von NumPy bietet verschiedene Methoden, um lineare Algebra auf jedes Numpy-Array anzuwenden. Sie finden: - Rangbestimmende Spur usw. eines Arrays.
- eigene Werte oder Matrizen
- Matrix- und Vektorprodukte (Punkt-Innen-Außen-Produkt usw.) Matrixpotenzierung
- Lösen Sie lineare oder Tensorgleichungen und vieles mehr!
Consider the example below which explains how we can use NumPy to do some matrix operations. Python import numpy as np A = np.array([[6 1 1] [4 -2 5] [2 8 7]]) print('Rank of A:' np.linalg.matrix_rank(A)) print('nTrace of A:' np.trace(A)) print('nDeterminant of A:' np.linalg.det(A)) print('nInverse of A:n' np.linalg.inv(A)) print('nMatrix A raised to power 3:n' np.linalg.matrix_power(A 3)) Rank of A: 3 Trace of A: 11 Determinant of A: -306.0 Inverse of A: [[ 0.17647059 -0.00326797 -0.02287582] [ 0.05882353 -0.13071895 0.08496732] [-0.11764706 0.1503268 0.05228758]] Matrix A raised to power 3: [[336 162 228] [406 162 469] [698 702 905]]
Let us assume that we want to solve this linear equation set: x + 2*y = 8 3*x + 4*y = 18
This problem can be solved using linalg.solve method as shown in example below: Python import numpy as np # coefficients a = np.array([[1 2] [3 4]]) # constants b = np.array([8 18]) print('Solution of linear equations:' np.linalg.solve(a b)) Solution of linear equations: [ 2. 3.]
Finally we see an example which shows how one can perform linear regression using least squares method. A linear regression line is of the form w1 x + w 2 = y und es ist die Linie, die die Summe der Quadrate des Abstands von jedem Datenpunkt zur Linie minimiert. Bei gegebenen n Datenpaaren (xi yi) sind die gesuchten Parameter w1 und w2, die den Fehler minimieren: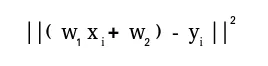 
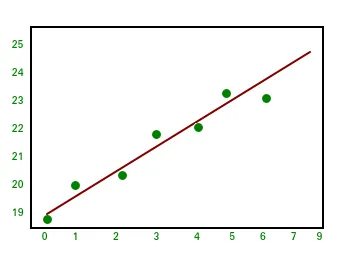
Let us have a look at the example below: Python import numpy as np import matplotlib.pyplot as plt # x co-ordinates x = np.arange(0 9) A = np.array([x np.ones(9)]) # linearly generated sequence y = [19 20 20.5 21.5 22 23 23 25.5 24] # obtaining the parameters of regression line w = np.linalg.lstsq(A.T y)[0] # plotting the line line = w[0]*x + w[1] # regression line plt.plot(x line 'r-') plt.plot(x y 'o') plt.show()
Dies führt zum Abschluss dieser Reihe von NumPy-Tutorials. NumPy ist eine weit verbreitete Allzweckbibliothek, die den Kern vieler anderer Berechnungsbibliotheken wie Scipy, Scikit-Learn, Tensorflow, Matplotlib, OpenCV usw. bildet. Ein grundlegendes Verständnis von NumPy hilft beim effizienten Umgang mit anderen Bibliotheken auf höherer Ebene! Referenzen: Quiz erstellen
In above example the scalar b is stretched to become an array of with the same shape as a so the shapes are compatible for element-by-element multiplication. Now let us see an example where both arrays get stretched. Python 
In manchen Fällen werden beim Broadcasting beide Arrays gedehnt, um ein Ausgabearray zu bilden, das größer ist als jedes der ursprünglichen Arrays.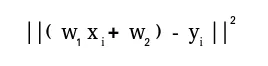 
Let us have a look at the example below: Python 
Dies führt zum Abschluss dieser Reihe von NumPy-Tutorials. NumPy ist eine weit verbreitete Allzweckbibliothek, die den Kern vieler anderer Berechnungsbibliotheken wie Scipy, Scikit-Learn, Tensorflow, Matplotlib, OpenCV usw. bildet. Ein grundlegendes Verständnis von NumPy hilft beim effizienten Umgang mit anderen Bibliotheken auf höherer Ebene! Referenzen: