Prozentsatz – In der Mathematik ist ein Prozentsatz eine Zahl oder ein Verhältnis, das einen Bruch von 100 angibt. Es handelt sich um eine Methode, die verwendet wird, um eine dimensionslose Beziehung zwischen zwei Zahlen auszudrücken, ähnlich wie Verhältnisse, Brüche und Dezimalzahlen. Prozentsätze werden üblicherweise durch das Symbol % nach der Zahl angegeben. Das Wort Prozentsatz wurde aus dem lateinischen Wort geprägt Pro hundert was bedeutet um hundert . Es handelt sich um eine dimensionslose Beziehung zwischen zwei Zahlen. Es wird oft durch das Zeichen gekennzeichnet % oder Prozent oder pct .
In diesem Artikel werden wir darauf eingehen Prozentsatz einschließlich seiner Definition, Beispiele, Prozentformel, Berechnung des Prozentsatzes usw.
Beispiele für Prozentsätze sind:
- 10 % sind 10/100, also 1/10 der Zahl
- 20 % sind 20/100, also 1/5 der Zahl
In diesem Artikel erfahren Sie mehr über Prozentsätze, Prozentformeln, die Berechnung von Prozentsätzen und vieles mehr.
Inhaltsverzeichnis
- Was ist Prozentsatz?
- Beispiele für Prozent
- Prozentformel
- Wie berechnet man den Prozentsatz einer Zahl?
- Prozentuale Differenzformel
- Formel zur prozentualen Erhöhung
- Formel für prozentuale Verringerung
- Wie berechnet man den Prozentsatz?
- Prozent in Bruch umwandeln
- Bruch in Prozent umwandeln
- Prozentdiagramm
- Prozenttabelle
- Unterschied zwischen Prozentsatz und Prozent
- Prozentsatz in Mathematik
- Prozent-Tricks
- So berechnen Sie den Prozentsatz der Noten
- Prozentrechner
- Gelöstes Beispiel für einen Prozentsatz
- Übungsfragen zum Thema Prozent
Was ist Prozentsatz?
Ein f Eine Fraktion, deren Nenner 100 ist, wird als Prozent bezeichnet Das heißt, bei allen Brüchen, bei denen der Nenner 100 ist, können wir den Nenner entfernen und das %-Zeichen setzen.
Zum Beispiel, Der Bruch 23/100 kann als 23 % geschrieben werden . Das Gegenteil gilt auch, d. h. jedes Prozentzeichen lässt sich leicht ersetzen, indem man die Zahl in einen Bruch mit dem Nenner 100 umwandelt. Beispielsweise können 45 % in einen Bruch als 45/100 umgewandelt werden.
- Prozentsätze werden auch genannt dimensionslose Zahlen , da sie keine Dimension haben. Sie sind das Verhältnis zweier Zahlen mit gleichen Abmessungen. Wenn wir 10 % einer Zahl sagen, bedeutet das 10 Prozent ihres Ganzen.
- Prozentsätze können auch sein dargestellt in Dezimalwerten wie 0,5 %, 0,75 % usw.
Überprüfen: Prozentsätze – Fragen und Antworten zur Eignung
Beispiele für Prozent
Einige Beispiele für Brüche sind: ,
- Wenn Kabir in der Mathematikprüfung 95 von 100 Punkten erreicht, wird der Bruchteil wie folgt geändert: 95/100 = 95 %
- Wenn Kandidat A 2450 von 10000 Stimmen erhält, wird dies in Prozent ausgedrückt als: 2450/1000 = 24,5/100 = 24,5 %
Ähnlich,
- 10/100 in Prozent = 10 %
- 50/100 in Prozent = 50 %
- 100/100 in Prozent = 100 %
Das Bild unten zeigt uns einige Beispiele, in denen der Prozentsatz verwendet wird.

Prozentformel
Prozentformel ist eine Formel, die verwendet wird, um den Betrag oder Anteil einer Menge in Hundert zu ermitteln. Für die Berechnung des Prozentsatzes benötigen wir also grundsätzlich drei Variablen. Zunächst der Gesamtwert V 1 , der Barwert V 2 und der Prozentwert P. Die algebraische Gleichung hierfür lautet:
Prozentsatz (P%) = (Teile (V 2 ) / Ganz (V 1 )) × 100

Wie berechnet man den Prozentsatz einer Zahl?
Die Berechnung des Prozentsatzes einer Zahl ist sehr einfach. Sie müssen lediglich die unten stehende Formel verwenden:
Prozent einer Zahl = Prozentsatz/100 × Zahl
Beispiel:
Berechnen Sie 5 % von 50
5 % von 50 = 5/100 × 50
5 % von 50 = 0,05 × 50
5 % von 50 = 2,50
Prozentuale Differenzformel
Prozentuale Differenz oder die prozentuale Veränderung Die Formel wird berechnet, wenn die Differenz zwischen zwei Werten durch den Durchschnitt derselben Werte dividiert wird. Wir können sagen, dass die prozentuale Differenz zur Berechnung der Wertänderung über den angegebenen Zeitraum verwendet wird. Mathematisch können wir geschrieben werden als:
Slice-Java-Array
Überprüfen: Grundkonzept des Prozentsatzes
Prozentuale Differenz = (Absolute Differenz / Durchschnitt) × 100
Beispiel: Der prozentuale Unterschied zwischen 50 und 100 beträgt:
= |50-100|/ {(50+100)/2} × 100
= 50/75 × 100
= 66,66 %
Sie wird als Verhältnis ausgedrückt und ist eine Zahl ohne Einheit
Formel zur prozentualen Erhöhung
Wir können die prozentuale Differenzformel verwenden, um die Änderung des Werts zu ermitteln, wenn er über einen bestimmten Zeitraum ansteigt. Der Formel zur prozentualen Erhöhung ist unten angegeben,
Prozentualer Anstieg = (Erhöhungswert – Originalwert / Durchschnitt) × 100
Formel für prozentuale Verringerung
Wir können die prozentuale Differenzformel verwenden, um die Änderung des Werts zu ermitteln, wenn er über einen bestimmten Zeitraum abnimmt. Der Formel zur prozentualen Verringerung ist unten angegeben,
Prozentuale Abnahme = (Ursprünglicher Wert – Abnahmewert / Durchschnitt) × 100
Notiz:
- Wenn der bei der Berechnung der prozentualen Erhöhungsformel erhaltene Wert negativ ist, handelt es sich tatsächlich um eine prozentuale Verringerung.
- Wenn der bei der Berechnung der prozentualen Verringerungsformel erhaltene Wert negativ ist, handelt es sich tatsächlich um eine prozentuale Erhöhung.
- Zur Ermittlung wird auch die prozentuale Änderung verwendet prozentuale Fehler in Mathematik, Physik und Chemie.
Wie berechnet man den Prozentsatz?
Die wichtigste Frage ist, wie man den Prozentsatz berechnet. Prozentsätze können also leicht berechnet werden, wenn die Werte als Brüche mit einem Nenner von 100 angegeben werden. Wenn nicht, müssen wir den angegebenen Bruch in einen Bruch mit einem Nenner von 100 umwandeln, und dann ist der Prozentsatz leicht zu berechnen.
Überprüfen: Wie berechnet man den Prozentsatz?
Wenn beispielsweise 65/100 als Prozentsatz berechnet werden soll, kann die Antwort leicht berechnet werden, indem man den Nenner 100 entfernt und das %-Symbol anwendet, also 65 %.
Beispiel: 0,76 in Prozent umrechnen.
Lösung:
0,76 = 0,76/1
0,76 = 76/100
0,76 = 76 %
Wie berechnet man den Prozentsatz, wenn die Gesamtsumme 100 beträgt?
Wenn sich der Gesamtwert in einem beliebigen Szenario auf 100 summiert, ist die Berechnung des Prozentsatzes sehr einfach, da die Zahl (im Zähler des Werts) selbst den Prozentsatz darstellt und das %-Symbol hinzugefügt wird.
Beispiel: Angenommen, Schüler A hat bei der Wahl eines Klassensprechers 69 Stimmen und Schüler B 31 Stimmen erhalten, dann ermitteln Sie den Prozentsatz der Stimmen, die A erhalten hat.
Lösung:
Gesamtstimmen = 69 + 31 = 100
A hat Stimmen = 69
Stimmen von A (in Prozent) = 69/100 = 69 %
Wie berechnet man den Prozentsatz, wenn die Gesamtsumme NICHT 100 beträgt?
Wenn der Gesamtwert in einem Szenario nicht 100 ergibt, wird der Prozentsatz berechnet, indem die Summe 100 im Bruch gebildet wird und dann die Zählerwerte zum Prozentsatz werden.
Beispiel: Angenommen, Kabir hätte 6 blaue Bälle, 8 rote Bälle und 6 gelbe Bälle – wie viel Prozent der roten Bälle hat er?
Lösung:
Gesamtzahl der Kugeln = rote Kugeln + blaue Kugeln + gelbe Kugeln
= 8 + 6 + 6 = 20 Bälle
Rote Kugeln = 8 Kugeln
Prozentsatz der roten Kugeln = 8/20
= (8/20) × (5/5) = 40/100 = 40 %
Prozent in Bruch umwandeln
In einigen Fällen erhalten wir den Prozentsatz und müssen ihn in a umrechnen Fraktion Nummer. Für die Umrechnung von Prozentsätzen in Brüche sind einige Berechnungen erforderlich. Wir können die Formel verwenden,
Überprüfen: Probleme mit Prozentsätzen
Bruch = Prozentsatz/100
Nachdem ich es bekommen habe, um es weiter zu reduzieren. Zum Beispiel,
- Bruchteil von 25 % = 25/100 = 1/4
- Bruchteil von 50 % = 50/100 = 1/2
- Bruchteil von 75 % = 75/100 = 3/4
- Bruchteil von 90 % = 90/100 = 9/10
Bruch in Prozent umwandeln
Um einen Bruch in einen Prozentsatz umzuwandeln, gehen wir davon aus, dass der Bruch durch a/b dargestellt wird, wobei a Teil des Ganzen b ist. Zähler und Nenner mit 100 multiplizieren.
Wir wissen, dass 1/100 = 1 %
Daher, Die Gleichung kann wie folgt geschrieben werden:
a/b × 100 %.
Somit, Um einen Bruch in einen Prozentsatz umzuwandeln, multiplizieren Sie den Bruch mit 100.
Prozentdiagramm
Sehen wir uns das Prozentdiagramm der in Prozente umgewandelten Brüche an.
Prozentdiagramm | |||
|---|---|---|---|
| Fraktion | Prozentsatz | Fraktion | Prozentsatz |
1/1 | 100% | 1/11 | 9,09 % |
1/2 | fünfzig% | 1/12 | 8,33 % |
1/3 | 33,33 % | 1/13 | 7,69 % |
1/4 | 25 % | 1/14 | 7,14 % |
1/5 | zwanzig% | 1/15 | 6,66 % |
1/6 | 16,66 % | 1/16 | 6,25 % |
1/7 | 14,28 % | 1/17 | 5,88 % |
1/8 | 12,5 % | 1/18 | 5,55 % |
1/9 | 11,11 % | 1/19 | 5,26 % |
1/10 | 10 % | 1/20 | 5 % |
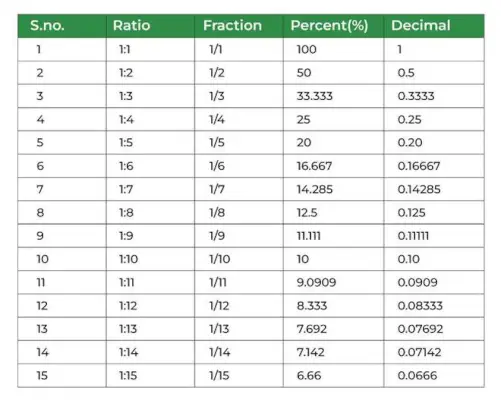
Prozenttabelle
Das unten hinzugefügte Bild zeigt die Prozenttabelle.
Unterschied zwischen Prozentsatz und Prozent
Die Wörter Prozent und Prozent hängen miteinander zusammen, aber es gibt einen Unterschied zwischen beiden. Prozent wird immer von einer Zahl begleitet, zum Beispiel 25 %.
Beim Prozentwert muss jedoch keine Zahl mit dem Begriff einhergehen.
Beispielsweise ist der Prozentsatz der Personen, die an der Abstimmung im Jahr 2022 teilgenommen haben, höher als der Prozentsatz der Personen, die im Jahr 2021 teilgenommen haben.
Brüche, Dezimalzahlen, Verhältnisse und Prozentsätze hängen auch miteinander zusammen.
Prozentsatz in Mathematik
In der Mathematik wird der Prozentsatz mit drei möglichen Unbekannten und Variablen geschrieben. Die drei Begriffe sind bekannt:
- Prozentsatz
- Teil
- Base
Beispielsweise sind 50 % von 400 200. Hier ist 50 der Prozentsatz, 400 die Basis und 200 ein Teil.
Beispiel: Wenn 25 % von 200 50 sind, erklären Sie die verschiedenen Begriffe in der Berechnung.
25 % von 400 sind 50. Hier ist 25 der Prozentsatz, 200 die Basis und 50 der Teil.
Im Bruch lässt es sich wie folgt schreiben:
Teil/Basis = 25/200 = 1/4
1/4 ist der erhaltene Bruchteil. Wir haben jedoch gelernt, wie man Brüche in Prozente umwandelt. Multiplizieren Sie daher 1/4 mit 100,
1/4 × 100 = 25 %.
Prozent-Tricks
Es gibt Prozenttricks, die bei der Berechnung des Prozentsatzes von Zahlen angewendet werden können. Der unten angegebene Trick ist der am häufigsten verwendete:
% x von y = % y von x
Beispiel: Lösen Sie 300 % von 50.
Hier kann es etwas langwierig und schwierig sein, 300 % von 50 zu lösen. Mit dem Trick lässt sich das Problem jedoch leicht lösen,
%x von y = %y von x
300 % von 50 = 50 % von 300
Nun ist es relativ einfach, 50 % von 300 zu lösen. 50 % von 300 sind nur die Hälfte von 300. Daher sind 50 % von 300 150.
Daher sind 300 % von 50 150.
So berechnen Sie den Prozentsatz der Noten
Der Prozentsatz wird meist bei der Notenberechnung für Studierende verwendet. Die Noten der Studierenden beziehen sich auf die Gesamtpunktzahl. Dieser Bruch wird in einen Prozentsatz umgewandelt, indem man ihn mit 100 multipliziert. Auf diese Weise können wir die Noten in Prozent berechnen. Sehen wir uns einige Beispiele für prozentuale Noten an:
| Noten erhalten | Gesamtnoten | Noten in Prozent (%) |
|---|---|---|
| fünfzig | 100 | 50/100 × 100 = 50 % |
| 25 | fünfzig | 25/50 × 100 = 50 % |
| 80 | 100 | 80/100 × 100 = 80 % |
| 33 | 100 | 33/100 × 100 = 33 % |
Prozentrechner
Der Prozentrechner ist ein kostenloses Tool, das unter bereitgestellt wird techcodeview.com Dies wird verwendet, um den Prozentsatz zu ermitteln, wenn zwei oder mehr Zahlen angegeben sind. Schauen Sie sich den Prozentrechner unten an:
Überprüfen: Prozentrechner
Mehr lesen,
- Brüche
- Verhältnis- und Proportionsformel
- Prozentuale Ertragsformel
Gelöstes Beispiel für einen Prozentsatz
Einige Beispiele für Prozentsätze sind:
Beispiel 1: Finden Sie 15 % von 500.
Lösung:
Wir können den Prozentsatz anhand der Formel ermitteln:
IN2= P × V1
IN2= 15 % × 500
IN2= (15 × 500) / 100
IN2= 75.
Somit sind 15 % von 500 75.
Überprüfen: Prozentfragen
Beispiel 2: Finden Sie 4 % von 1300.
Lösung:
Wir können den Prozentsatz anhand der Formel ermitteln:
IN2= P × V1
IN2= 4 % × 1300
IN2= (4 × 1300) / 100
IN2= 52.
Somit sind 4 % von 1300 52.
Beispiel 3: Wie viel Prozent ist 1 von 3000?
Lösung:
Wir können den Prozentsatz anhand der Formel ermitteln:
IN2= P × V1
P = V2/ IN1
P = 1 / 3000
Somit ist P% = 1/3000 × 100
P% = (1/30)%
Somit ist (1/30) % von 2000 500.
Beispiel 4: Wenn 10 % von x 900 sind. Finden Sie x.
Lösung:
Wir können den Prozentsatz anhand der Formel ermitteln:
IN2= P × V1
IN1= V2/ P
IN1= (V2× 100 ) / P%
IN1= (900 × 100) / 10
IN1= 9000
Somit beträgt der Wert von x 9000.
Beispiel 5: Ermitteln Sie jeweils den Wert des Prozentsatzes grüner Blöcke.
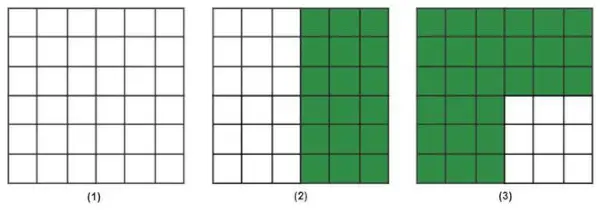
Lösung:
Im ersten Fall sind die grünen Blöcke 0 und die Gesamtzahl der Blöcke beträgt 36.
Daher,
Prozentsatz der grünen Blöcke = 0/36 × 100 = 0 %.
Im zweiten Fall sind es 18 grüne Blöcke und insgesamt 36 Blöcke.
Daher,
Prozentsatz der grünen Blöcke = 18/36 × 100 = 50 %.
Im dritten Fall beträgt die Anzahl der grünen Blöcke 27 und die Gesamtzahl der Steine 36.
Daher,
Prozentsatz der grünen Blöcke = 27/36 × 100 = 75 %.
Beispiel 6: Wie viel Prozent sind 15 von 50?
Ursprünglicher Wert = 15
Gesamtwert = 50
Die Prozentformel lautet:
Prozentsatz = (Ursprünglicher Wert/Gesamtwert) × 100
= 15/50 × 100
= 30 %
Beispiel 7: Wie viel Prozent von 80 ist 20?
Ursprünglicher Wert = 20
Gesamtwert = 80
Die Prozentformel lautet:
Prozentsatz = (Ursprünglicher Wert/Gesamtwert) × 100
= 20/80 × 100
= 25 %
Übungsfragen zum Thema Prozent
F1: Ein Junge hat 450 von insgesamt 500 Mark bekommen. Finden Sie den Prozentsatz der Noten.
F2: Ermitteln Sie den Prozentsatz an reinen Goldpartikeln in 18 Karat Gold, vorausgesetzt, 24 Karat sind reines Gold.
F3: Eine 5-Liter-Säureflasche hat eine Konzentration von 10 %. Finden Sie die Konzentration der reinen Säure in der Lösung.
F4: Ram hat 223 von 600 Punkten erreicht und die Prüfung mit 17 Punkten nicht bestanden. Finden Sie den Prozentsatz der bestandenen Noten.
Fazit – Prozentsatz
Prozentangaben sind wie eine universelle Sprache für Proportionen. Anstatt sich mit Brüchen oder Dezimalzahlen herumzuschlagen, können wir verwenden Prozentsätze, um einen beliebigen Teil eines Ganzen von 100 auszudrücken . So wird das Vergleichen zum Kinderspiel, ob es darum geht, Rabatte auf einen Verkauf zu verstehen , Umfrageergebnisse visualisieren oder einem Rezept folgen. Von alltäglichen Aufgaben bis hin zu komplexen Datenanalysen sind Prozentsätze ein leistungsstarkes Werkzeug, um unsere Welt Stück für Stück zu verstehen.
FAQs zum Thema Prozentsatz
Was ist ein Prozentsatz von 100 %?
Ein Prozentsatz von 100 % ist eigentlich 100 selbst
Wie definiert man Prozent?
Ein Prozentsatz ist eine Möglichkeit, einen Teil einer Sache im Vergleich zum Ganzen auszudrücken, geschrieben als Bruchteil von 100.
Wie viel Prozent eines Jahres ist ein Tag?
Um den Prozentsatz eines Jahres zu berechnen, den ein Tag darstellt, können wir die Anzahl der Tage in einem Tag durch die Anzahl der Tage in einem Jahr dividieren und dann mit 100 % multiplizieren (um es als Prozentsatz auszudrücken).
Was ist der CGPA-Prozentsatz?
Die Umrechnung von CGPA in Prozent ist so einfach wie die Multiplikation Ihres CGPA mit 9,5.
Was ist Prozentsatz?
„Prozent“ ist die Darstellung von Zahlen. Die wörtliche Bedeutung des Wortes „Prozentsatz“ liegt zwischen 100 und 100. In Prozent wird der Wert zwischen 100 und 100 dargestellt.
Was ist das Symbol für Prozent?
Das Prozentzeichen ist %. Es wird auch als Prozent bezeichnet.
Wie berechnet man den Prozentsatz?
Um den Prozentsatz einer Zahl zu berechnen, dividieren Sie einfach die erhaltene Zahl durch die Gesamtzahl und multiplizieren Sie den Bruch mit 100
Was ist eine prozentuale Änderung?
Die prozentuale Änderung einer Zahl ist die prozentuale Änderung vom alten Wert zum neuen Wert. Es wird nach der Formel berechnet:
Prozentuale Änderung = {(Differenz zwischen altem und neuem Wert) / alter Wert} × 100.
Was sind Beispiele für Prozentsätze?
Prozentsätze werden in unserem täglichen Leben sehr oft verwendet. Hier sind einige Beispiele für die Verwendung von Prozentsätzen im wirklichen Leben.
- Der Prozentsatz der verschiedenen Nährstoffarten ist auf der Rückseite der Lebensmittelverpackungen angegeben.
- Der Akku zeigt in unseren Telefonen seine Leistung in Prozent an.
- Prozentsatz der von den Studierenden in der Prüfung erzielten Noten.
Kann der Prozentsatz 100 überschreiten?
Ja, der Prozentwert kann mehr als 100 betragen, wenn der angegebene Wert größer als der ursprüngliche Wert ist. Beispielsweise entspricht 40/20 200 %.
