Das Quantil-Quantil-Diagramm (q-q-Diagramm) ist eine grafische Methode zur Bestimmung, ob ein Datensatz einer bestimmten Wahrscheinlichkeitsverteilung folgt oder ob zwei Datenstichproben aus derselben stammen Bevölkerung oder nicht. Q-Q-Diagramme sind besonders nützlich, um zu beurteilen, ob ein Datensatz vorhanden ist normal verteilt oder wenn es einer anderen bekannten Distribution folgt. Sie werden häufig in der Statistik, Datenanalyse und Qualitätskontrolle verwendet, um Annahmen zu überprüfen und Abweichungen von erwarteten Verteilungen zu identifizieren.
Quantile und Perzentile
Quantile sind Punkte in einem Datensatz, die die Daten in Intervalle unterteilen, die gleiche Wahrscheinlichkeiten oder Anteile der Gesamtverteilung enthalten. Sie werden häufig verwendet, um die Ausbreitung oder Verteilung eines Datensatzes zu beschreiben. Die häufigsten Quantile sind:
- Median (50. Perzentil) : Der Median ist der Mittelwert eines Datensatzes, wenn er vom kleinsten zum größten geordnet wird. Es teilt den Datensatz in zwei gleiche Hälften.
- Quartile (25., 50. und 75. Perzentil) : Quartile teilen den Datensatz in vier gleiche Teile. Das erste Quartil (Q1) ist der Wert, unter den 25 % der Daten fallen, das zweite Quartil (Q2) ist der Median und das dritte Quartil (Q3) ist der Wert, unter den 75 % der Daten fallen.
- Perzentile : Perzentile ähneln Quartilen, teilen den Datensatz jedoch in 100 gleiche Teile. Beispielsweise ist das 90. Perzentil der Wert, unter den 90 % der Daten fallen.
Notiz:
- Ein q-q-Diagramm ist ein Diagramm der Quantile des ersten Datensatzes gegenüber den Quantilen des zweiten Datensatzes.
- Zu Referenzzwecken ist auch eine 45 %-Linie eingezeichnet; Für Wenn die Stichproben aus derselben Grundgesamtheit stammen, liegen die Punkte entlang dieser Linie.
Normalverteilung:
Die Normalverteilung (auch bekannt als Gaußsche Verteilungs-Bell-Kurve) ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die eine Verteilung darstellt, die aus den zufällig generierten realen Werten erhalten wird.
. 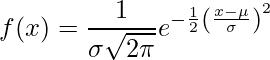

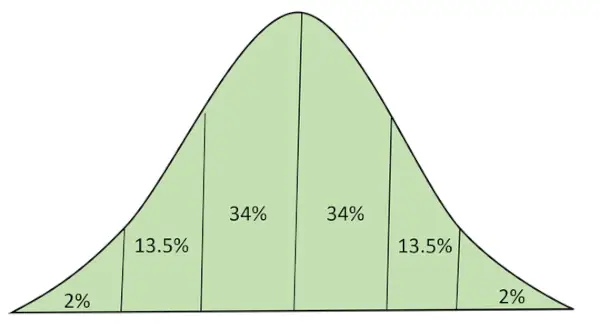
Normalverteilung mit Fläche unter der Kurve
Wie zeichnet man ein Q-Q-Diagramm?
Um ein Quantil-Quantil-Diagramm (Q-Q) zu zeichnen, können Sie die folgenden Schritte ausführen:
- Sammeln Sie die Daten : Sammeln Sie den Datensatz, für den Sie das Q-Q-Diagramm erstellen möchten. Stellen Sie sicher, dass die Daten numerisch sind und eine Zufallsstichprobe aus der interessierenden Grundgesamtheit darstellen.
- Sortieren Sie die Daten : Ordnen Sie die Daten entweder in aufsteigender oder absteigender Reihenfolge an. Dieser Schritt ist für die genaue Berechnung von Quantilen unerlässlich.
- Wählen Sie eine theoretische Verteilung : Bestimmen Sie die theoretische Verteilung, mit der Sie Ihren Datensatz vergleichen möchten. Zu den gängigen Optionen gehören die Normalverteilung, die Exponentialverteilung oder jede andere Verteilung, die gut zu Ihren Daten passt.
- Berechnen Sie theoretische Quantile : Berechnen Sie die Quantile für die gewählte theoretische Verteilung. Wenn Sie beispielsweise einen Vergleich mit einer Normalverteilung durchführen, würden Sie die inverse kumulative Verteilungsfunktion (CDF) der Normalverteilung verwenden, um die erwarteten Quantile zu ermitteln.
- Plotten :
- Tragen Sie die sortierten Datensatzwerte auf der x-Achse ein.
- Tragen Sie die entsprechenden theoretischen Quantile auf der y-Achse ein.
- Jeder Datenpunkt (x, y) stellt ein Paar beobachteter und erwarteter Werte dar.
- Verbinden Sie die Datenpunkte, um die Beziehung zwischen dem Datensatz und der theoretischen Verteilung visuell zu überprüfen.
Interpretation des Q-Q-Diagramms
- Wenn die Punkte im Diagramm ungefähr entlang einer geraden Linie liegen, deutet dies darauf hin, dass Ihr Datensatz der angenommenen Verteilung folgt.
- Abweichungen von der Geraden weisen auf Abweichungen von der angenommenen Verteilung hin und erfordern weitere Untersuchungen.
Untersuchung der Verteilungsähnlichkeit mit Q-Q-Diagrammen
Die Untersuchung der Verteilungsähnlichkeit mithilfe von Q-Q-Diagrammen ist eine grundlegende Aufgabe in der Statistik. Der Vergleich zweier Datensätze, um festzustellen, ob sie aus derselben Verteilung stammen, ist für verschiedene Analysezwecke von entscheidender Bedeutung. Wenn die Annahme einer gemeinsamen Verteilung zutrifft, kann das Zusammenführen von Datensätzen die Genauigkeit der Parameterschätzung verbessern, beispielsweise für Standort und Maßstab. Q-Q-Plots, kurz für Quantil-Quantil-Plots, bieten eine visuelle Methode zur Beurteilung der Verteilungsähnlichkeit. In diesen Diagrammen werden Quantile aus einem Datensatz gegen Quantile aus einem anderen Datensatz aufgetragen. Wenn die Punkte entlang einer diagonalen Linie eng ausgerichtet sind, deutet dies auf eine Ähnlichkeit zwischen den Verteilungen hin. Abweichungen von dieser diagonalen Linie weisen auf Unterschiede in den Verteilungseigenschaften hin.
Während Tests wie die Chi-Quadrat Und Kolmogorov-Smirnov Tests können allgemeine Verteilungsunterschiede bewerten, Q-Q-Diagramme bieten eine differenzierte Perspektive durch den direkten Vergleich von Quantilen. Dies ermöglicht es Analysten, spezifische Unterschiede zu erkennen, wie z. B. Ortsverschiebungen oder Größenänderungen, die bei formalen statistischen Tests allein möglicherweise nicht erkennbar sind.
Python-Implementierung des Q-Q-Plots
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Ausgabe:
Q-Q-Diagramm
Da die Datenpunkte im Q-Q-Diagramm ungefähr einer geraden Linie folgen, deutet dies darauf hin, dass der Datensatz mit der angenommenen theoretischen Verteilung übereinstimmt, die wir in diesem Fall als Normalverteilung angenommen haben.
Vorteile des Q-Q-Diagramms
- Flexibler Vergleich : Q-Q-Diagramme können Datensätze unterschiedlicher Größe ohne vergleichen gleiche Stichprobengrößen erforderlich.
- Dimensionslose Analyse : Sie sind dimensionslos und daher für den Vergleich von Datensätzen geeignet verschiedene Einheiten oder Maßstäbe.
- Visuelle Interpretation : Bietet eine klare visuelle Darstellung der Datenverteilung im Vergleich zu einer theoretischen Verteilung.
- Empfindlich gegenüber Abweichungen : Erkennt problemlos Abweichungen von angenommenen Verteilungen und hilft so bei der Identifizierung von Datendiskrepanzen.
- Diagnosehilfsmittel : Hilft bei der Beurteilung von Verteilungsannahmen, der Identifizierung von Ausreißern und dem Verständnis von Datenmustern.
Anwendungen des Quantil-Quantil-Diagramms
Das Quantil-Quantil-Diagramm wird für folgenden Zweck verwendet:
- Bewertung von Verteilungsannahmen : Q-Q-Diagramme werden häufig verwendet, um visuell zu überprüfen, ob ein Datensatz einer bestimmten Wahrscheinlichkeitsverteilung folgt, beispielsweise der Normalverteilung. Durch den Vergleich der Quantile der beobachteten Daten mit den Quantilen der angenommenen Verteilung können Abweichungen von der angenommenen Verteilung erkannt werden. Dies ist bei vielen statistischen Analysen von entscheidender Bedeutung, bei denen die Gültigkeit von Verteilungsannahmen Auswirkungen auf die Genauigkeit statistischer Schlussfolgerungen hat.
- Ausreißer erkennen : Ausreißer sind Datenpunkte, die erheblich vom Rest des Datensatzes abweichen. Q-Q-Diagramme können dabei helfen, Ausreißer zu identifizieren, indem sie Datenpunkte aufdecken, die weit vom erwarteten Muster der Verteilung abweichen. Ausreißer können als Punkte erscheinen, die von der erwarteten geraden Linie im Diagramm abweichen.
- Vergleich von Verteilungen : Mit Q-Q-Diagrammen können zwei Datensätze verglichen werden, um festzustellen, ob sie aus derselben Verteilung stammen. Dies wird erreicht, indem die Quantile eines Datensatzes gegen die Quantile eines anderen Datensatzes aufgetragen werden. Wenn die Punkte ungefähr entlang einer geraden Linie liegen, deutet dies darauf hin, dass die beiden Datensätze aus derselben Verteilung stammen.
- Beurteilung der Normalität : Q-Q-Diagramme eignen sich besonders zur Beurteilung der Normalität eines Datensatzes. Wenn die Datenpunkte im Diagramm genau einer geraden Linie folgen, weist dies darauf hin, dass der Datensatz annähernd normalverteilt ist. Abweichungen von der Linie deuten auf Abweichungen von der Normalität hin, die möglicherweise weitere Untersuchungen oder nichtparametrische statistische Techniken erfordern.
- Modell Bestätigung : In Bereichen wie Ökonometrie und maschinellem Lernen werden Q-Q-Diagramme zur Validierung von Vorhersagemodellen verwendet. Durch den Vergleich der Quantile der beobachteten Reaktionen mit den von einem Modell vorhergesagten Quantilen kann man beurteilen, wie gut das Modell zu den Daten passt. Abweichungen vom erwarteten Muster können auf Bereiche hinweisen, in denen das Modell verbessert werden muss.
- Qualitätskontrolle : Q-Q-Diagramme werden in Qualitätskontrollprozessen eingesetzt, um die Verteilung gemessener oder beobachteter Werte über die Zeit oder über verschiedene Chargen hinweg zu überwachen. Abweichungen von den erwarteten Mustern in der Darstellung können auf Veränderungen in den zugrunde liegenden Prozessen hinweisen und Anlass zu weiteren Untersuchungen geben.
Arten von Q-Q-Diagrammen
Es gibt verschiedene Arten von Q-Q-Diagrammen, die üblicherweise in der Statistik und Datenanalyse verwendet werden und sich jeweils für unterschiedliche Szenarien oder Zwecke eignen:
- Normalverteilung : Eine symmetrische Verteilung, bei der das Q-Q-Diagramm Punkte ungefähr entlang einer diagonalen Linie anzeigen würde, wenn die Daten einer Normalverteilung entsprechen.
- Rechtsschiefe Verteilung : Eine Verteilung, bei der das Q-Q-Diagramm ein Muster anzeigt, bei dem die beobachteten Quantile von der geraden Linie zum oberen Ende hin abweichen, was auf einen längeren Schwanz auf der rechten Seite hinweist.
- Linksschiefe Verteilung : Eine Verteilung, bei der das Q-Q-Diagramm ein Muster aufweist, bei dem die beobachteten Quantile von der geraden Linie zum unteren Ende hin abweichen, was auf einen längeren Schwanz auf der linken Seite hinweist.
- Unterstreute Verteilung : Eine Verteilung, bei der das Q-Q-Diagramm beobachtete Quantile im Vergleich zu den theoretischen Quantilen enger um die diagonale Linie gruppieren würde, was auf eine geringere Varianz hindeutet.
- Überstreute Verteilung : Eine Verteilung, bei der das Q-Q-Diagramm beobachtete Quantile stärker verteilt oder von der diagonalen Linie abweichend anzeigt, was auf eine höhere Varianz oder Streuung im Vergleich zur theoretischen Verteilung hinweist.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Ausgabe:
Q-Q-Diagramm für verschiedene Verteilungen
Java-Iterate-Karte
