Die Steigungsformel wird verwendet, um die Steilheit oder Neigung einer Linie zu bestimmen. Zur Berechnung der Steigung einer Geraden werden die x- und y-Koordinaten der auf der Geraden liegenden Punkte herangezogen. Die Änderung der y-Koordinate im Verhältnis zur Änderung der x-Koordinaten wird Steigung einer Geraden genannt und üblicherweise mit dem Buchstaben m dargestellt.

Inhaltsverzeichnis

• Was ist die Steigungsformel?
• Steigungsformel
• Ableitung der Steigungsformel
• Formel für die Steigung einer Geraden (Gerade).
• Steigungsgleichung
• Beispiel für eine Steigungsformel

Was ist die Steigungsformel?

Zur Berechnung der Neigung einer Linie ist eine Steigungsformel erforderlich. Zur Berechnung der Steigung einer Geraden werden die x- und y-Koordinaten der Punkte auf der Geraden benötigt. Das Verhältnis der Änderung der Y-Koordinaten zur Änderung der X-Koordinaten wird als Steigung einer Geraden bezeichnet.

Steigung (m) = Änderung in y/Änderung in x = Δy/Δx

Steigungsformel

In der Mathematik wird die Steigung einer Linie verwendet, um zu bestimmen, wie stark die Linie geneigt ist, d. h. um die Steilheit einer Linie. Um die Steigung einer Geraden zu bestimmen, benötigen wir die x- und y-Koordinaten der auf der Geraden liegenden Punkte. Die Steigungsformel ist die Nettoänderung der Y-Koordinate geteilt durch die Nettoänderung der X-Koordinate. Δy ist die Änderung der y-Koordinaten und Δx ist die Änderung der x-Koordinaten. Daher ist das Verhältnis der Änderung der y-Koordinaten zur Änderung der x-Koordinaten gegeben durch:

Steigung (m) = Änderung in y/Änderung in x = Δy/Δx

m= (und ₂ - Und ₁ )/(X ₂ - X ₁ )

Wo

• X₁und x₂sind die Koordinaten der X-Achse
• Und₁Andy₂sind die Koordinaten der Y-Achse

Ableitung der Steigungsformel

Die x- und y-Koordinaten der Linie werden zur Berechnung der Steigung der Linie verwendet. Die Nettoänderung der y-Koordinate beträgt Δy, während die Nettoänderung der x-Koordinate Δx beträgt. Die Änderung der y-Koordinate in Bezug auf die Änderung der x-Koordinate kann also wie folgt geschrieben werden:

m = Δy/Δx

Wo,

• M ist die Steigung
• Δy ist die Änderung der y-Koordinaten
• Δx ist die Änderung der x-Koordinaten

Wir wissen, dass tan θ auch die Steigung der Linie ist, wobei θ der Winkel ist, den die Linie mit der positiven Richtung der x-Achse bildet.

Und, tan θ = Höhe/Basis

Da die Höhe/Basis zwischen zwei beliebigen Punkten = (y₂- Und₁)/(X₂- X₁)

Somit lautet die Steigungsgleichung: m = tan θ = Δy/Δx

Aus der Grafik sehen wir:

mvc mit Java

Δy = (y₂- Und₁)

Δx = (x₂- X₁)

Dann lautet die Steigungsformel:

Steigung = m = (y ₂ - Und ₁ )/(X ₂ - X ₁ )

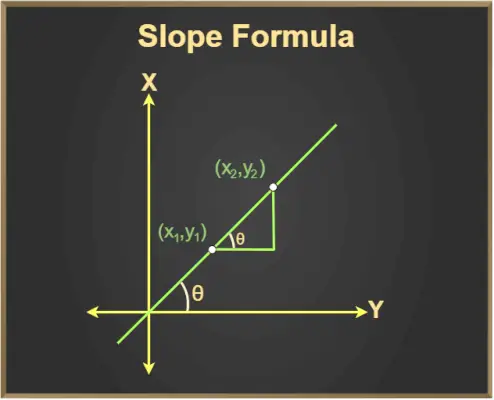
Formel für die Steigung einer Geraden (Gerade).

• Wir wissen das tan θ ist auch eine Steigung der Geraden, daher kann die Steigung einer Geraden auch dargestellt werden als:

Steigung (m) = tan θ = Δy/Δx

String-Array c

Wo ich ist der Winkel, den die Linie zur positiven X-Achse bildet,

• Δy = Änderung der y-Koordinaten,
• Δx = Änderung der x-Koordinaten.

• Wir können die Steigung einer Linie auch als das Verhältnis von Anstieg zu Verlauf definieren.

Steigung (m) = Steigung/Strecke

• Sei ax + by + c = 0 die allgemeine Gleichung einer Geraden. Die Formel für die Steigung der Geraden lautet nun:

Steigung (m) = – Koeffizient von x / Koeffizient von y = -a/b

• Die Steigungs-Achsenabschnitt-Form einer Linie unter Verwendung der Liniengleichung ist gegeben als:

y = mx + c

Wo M ist die Steigung der Linie und c ist der y-Achsenabschnitt der Linie.

Steigungsgleichung

Die Steigungsformel wird verwendet, um die Steigung einer Linie zu bestimmen. Die Gleichung, die zur Bestimmung der Steigung verwendet wird, lautet wie folgt:

m = tanθ = Δy/Δx = (y ₂ - Und ₁ )/(X ₂ - X ₁ )

Wo,

• M ist die Steigung der Linie
• Δy ist der Unterschied in den y-Koordinaten
• Δx ist der Unterschied in den x-Koordinaten
• ich ist der Winkel, den die Linie mit der positiven x-Achse bildet

Die Gleichung der Geraden mit der Steigung m ist gegeben durch:

y = mx + c

Wo,

• M ist die Steigung der Linie
• B ist der y-Achsenabschnitt der Linie

Mehr lesen,

• Parallele Linien
• Steigungsschnittform

Beispiel für eine Steigungsformel

Beispiel 1: Ermitteln Sie die Steigung einer Geraden mit den Koordinaten (3, 7) und (5, 8).

Lösung:

Gegeben ist (x₁, Und₁) = (3,7) und (x₂, Und₂) = (5.8)

Steigungsformel (m) = (y ₂ - Und ₁ )/(X ₂ - X ₁ )

⇒ m = (8 – 7)/(5 – 3) = 1/2

Daher beträgt die Steigung der gegebenen Geraden 1/2.

Beispiel 2: Bestimmen Sie die Steigung einer Geraden mit den Koordinaten (7, -5) und (2, -3).

Lösung:

Gegeben ist (x₁, Und₁) = (7, -5) und (x₂, Und₂) = (23)

Steigungsformel (m) = (y ₂ - Und ₁ )/(X ₂ - X ₁ )

⇒ m = (-3 – (-5))/(2 – 7) = -2/5

Konvertieren Sie int in Double Java

Daher beträgt die Steigung der gegebenen Linie -2/5

Beispiel 3: Ermitteln Sie den Wert von a, wenn die Steigung einer Geraden, die durch die Punkte (-4, a) und (2, 5) verläuft, 3 beträgt.

Lösung:

Gegeben ist (x₁, Und₁) = (4,a) und (x₂, Und₂) = (2, 5) und Steigung (m) = 3

Wir wissen, dass Steigung (m) = (y ₂ - Und ₁ )/(X ₂ - X ₁ )

Java-Boolescher String

⇒ 3 = (5 – a)/(2 – 4)

⇒ 3 = (5 – a)/(-2)

⇒ -6 = 5 – a ⇒ a = 5 + 6 = 11

Daher ist der Wert von a = 11

Beispiel 4: Wenn eine Linie mit der positiven Y-Achse einen Winkel von 60° bildet, welchen Wert hat dann die Steigung der Linie?

Lösung:

Gegebene Daten: Winkel, der durch eine Linie mit der positiven Y-Achse entsteht = 60°

Wir wissen: Wenn die Linie einen Winkel von 60° zur positiven y-Achse bildet, dann bildet sie mit der x-Achse einen Winkel von (90° – 60° = 30°).

Daher ist der Wert der Steigung der Linie (m) = tan 30° = 1/√3

Daher ist der Wert der Steigung der Geraden = 1/√3.

Beispiel 5: Sheela überprüfte eine Grafik und stellte fest, dass der Raise 12 Einheiten und der Run 4 Einheiten betrug. Berechnen Sie nun die Steigung einer Geraden.

Lösung:

Bei gegebenen Daten beträgt der Anstieg = 12 Einheiten und der Lauf = 4 Einheiten

Wir wissen, dass Steigung (m) = Steigung/Strecke

⇒ m = 12/4 = 3

Daher beträgt die Steigung der gegebenen Geraden 3

Beispiel 6: Ermitteln Sie die Steigung der Geraden 3x – 7y + 8 = 0.

Lösung:

Gegebene Daten: Die Gleichung der Linie = 3x – 7y + 8 = 0

Vergleichen Sie nun das Gegebene mit der allgemeinen Geradengleichung, d. h. ax + by + c = 0

Daher ist a = 3, b = -7 und c = 8

wie man von string nach int konvertiert

Wir wissen, dass Steigung (m) = – Koeffizient von x/Koeffizient von y = –a/b

⇒ m = -3/(-7) = 3/7

Daher beträgt die Steigung der gegebenen Geraden 3/7.

Übungsfragen zur Steigungsformel

Q1. Berechnen Sie die Steigung einer Geraden, die durch die Punkte (2, 3) und (5, 7) verläuft.

Q2. Wie groß ist die Steigung einer Geraden mit der Gleichung y = 3x – 11?

Q3. Wenn die Steigung einer Geraden 5/6 beträgt und sie durch den Punkt (2, 5) verläuft, wie lautet dann die Gleichung der Geraden in Steigungs-Achsenabschnitts-Form?

Q4. Berechnen Sie die Steigung einer Geraden parallel zur Geraden (0, -3) und (1, 11)

F5. Welche Schlussfolgerungen können Sie über die Gerade ziehen, wenn die Steigung einer Geraden undefiniert ist?

FAQs zur Steigungsformel

Was ist die Steigung einer Linie?

Die Steigung einer Linie ist der Wert der Steilheit oder Neigung einer Linie in der x-y-Ebene. Die Steigung wird mit unterschiedlichen Methoden berechnet, je nachdem, ob die Gleichung der Geraden oder die Koordinaten der Punkte auf der Geraden angegeben werden.

Wie lautet die Formel, um die Steigung einer Tangentenformel zu ermitteln?

Die Steigung einer Linie wird anhand der angegebenen Formel berechnet. Angenommen, die gegebenen Koordinaten zweier auf der Geraden liegender Punkte seien (x₁, Und₁)/(X_2,Und₂). Dann lautet die Formel: Steigung = m = tan θ = (y ₂ - Und ₁ )/(X ₂ - X ₁ )

Was ist die Definition der Steigungsformel?

Die Steigungsformel ist definiert als:

• Steigung = (Änderung der Y-Koordinate)/(Änderung der X-Koordinate)
• Steigung = Steigung/Lauf.

Was ist die Steigung einer Diagrammformel?

Die Steigung einer Linie ist das Maß ihrer Neigung zur positiven x-Achse. Mathematisch ist die Steigung definiert als Aufstieg über Lauf .