Die Quadratwurzel aus 3 ist eine positive reelle Zahl, die bei Multiplikation mit sich selbst die Zahl 3 ergibt. Die Quadratwurzel aus 3 ist eine irrationale Zahl, da es sich um eine nicht endende und sich nicht wiederholende Dezimalzahl handelt. Die Quadratwurzel aus 3 wird als √3 oder 3 bezeichnet1/2. Da das Quadrat von 3 eine irrationale Zahl ist, wird sein exakter Dezimalwert nie berechnet.
Wert der Quadratwurzel von 3, √3 =1,732 (abgeschnitten)
In diesem Artikel lernen wir die Quadratwurzel aus 3 im Detail kennen.
Inhaltsverzeichnis
- Was ist die Quadratwurzel aus 3?
- Wurzel-3-Wert in der Mathematik
- Ist die Quadratwurzel aus 3 rational oder irrational?
- Wie finde ich die Quadratwurzel aus 3?
- Eigenschaften der Quadratwurzel einer Zahl
- Tabelle der Quadratwurzel
Was ist die Quadratwurzel aus 3?
Die Quadratwurzel einer Zahl ist eine Zahl, die, wenn sie mit sich selbst multipliziert wird, die ursprüngliche Zahl ergibt.
Beispiel: Die Quadratwurzel von 16 ist 4, da 4×4 = 16, also √16 = 4
Die Quadratwurzel von 3 oder einfach Wurzel 3 genannt ist eine irrationale Zahl, die durch Multiplikation mit sich selbst die Zahl 3 ergibt. Wir können den ungefähren Wert von Wurzel 3 wie folgt angeben:
- Dezimalform: 1,732
- Exponentenform: 31/2
- Radikalform: √3
Wurzel-3-Wert in der Mathematik
In der Mathematik ist es sehr wichtig, die Quadratwurzel einer beliebigen Zahl zu finden; die Quadratwurzel des perfekten Quadrats lässt sich leicht berechnen. Bei unvollständigen Quadraten ist das Finden einer Quadratwurzel schwierig und wird im Allgemeinen mithilfe der Methode der langen Division berechnet.
Die Wurzel von 3 wird als √3 ausgedrückt. Sie ist eine irrationale Zahl, sodass ihr Dezimalwert niemals berechnet werden kann. Es wird in der Radikalform als (3) dargestellt½. Die Quadratwurzel aus 3, aufgerundet auf 7 Dezimalstellen, ist 1,7320508.
Quadratwurzel von 3 = 1,7320508075688772…
Ist die Quadratwurzel aus 3 rational oder irrational?
Die Quadratwurzel 3 ist eine nicht endende und sich nicht wiederholende Dezimalzahl, und alle nicht endenden und sich nicht wiederholenden Dezimalzahlen fallen unter die irrationale Zahl. Man kann also mit Sicherheit sagen, dass √3 ein ist irrationale Zahl .
Die Dezimalentwicklung der Quadratwurzel aus 3 ist:
Zusammenführungssortierung Java
√3 = 1,7320508075688772…
Da es sich nicht wiederholt und nicht endet, können wir mit Sicherheit sagen, dass √3 irrational ist.
Wie finde ich die Quadratwurzel aus 3?
Es ist immer einfacher, die Quadratwurzel perfekter Quadrate zu berechnen, aber um die Quadratwurzel eines nicht perfekten Quadrats zu berechnen, müssen wir die Methode der langen Division durchführen.
Um die Quadratwurzel aus 3 zu berechnen, müssen wir die folgenden Schritte ausführen:
Schritt 1: Schreiben Sie 3 als 3,000000 (wobei Nullen immer in Form von Paaren gehalten werden), um die Division zu erleichtern.
Schritt 2: Suchen Sie nun das perfekte Quadrat kleiner als 3, also 1, und dividieren Sie die Zahl durch dieses.
Schritt 3: Jetzt ist der Quotient 1 und der Rest ist 2. Wir werden eine Dezimalstelle in den Quotienten einfügen und das Nullenpaar für die weitere Division nach unten ziehen.
Schritt 4: Jetzt ist der nächste Dividend 200, addiert wird der nächste Divisor 2X (Quotient 1 wird zum vorherigen Divisor 1 addiert und X steht an der zehnten Stelle), so dass die Multiplikation der Zahl 2X und X kleiner als 200 sein sollte. Das ergibt der nächste Wert 27 als neuer Teiler.
Schritt 5: Jetzt wird nach einer Dezimalstelle 7 zum Quotienten addiert, sodass der Wert des Quotienten 1,7 beträgt und der neue Teiler durch Addition von 7 zu 27, also 34Y, erhalten wird, wobei Y an der Hundertstelstelle steht. Mit den vorherigen Schritten können wir fortfahren und die Quadratwurzel aus 3 im Quotienten ermitteln.
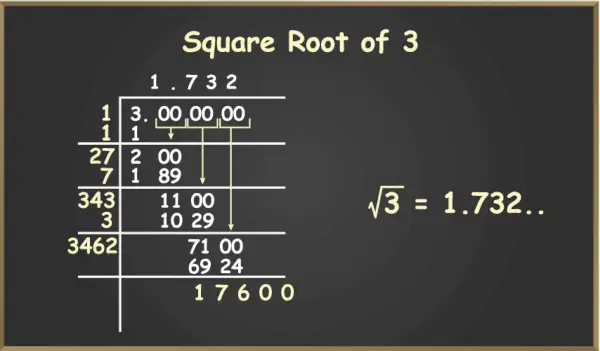
Quadratwurzel von 3
Bringen Sie nun das nächste Nullenpaar nach unten und wiederholen Sie die Schritte 4 und 5. Dies ist für unendlich viele Schritte möglich, da der genaue Wert der Quadratwurzel aus 2 bis auf unendlich viele Dezimalstellen reicht. Wir können das Ergebnis mit bis zu 4 Dezimalstellen berechnen, da es für ca. Wert der Quadratwurzel.
Eigenschaften der Quadratwurzel einer Zahl
Im Folgenden werden verschiedene Eigenschaften der Quadratwurzel einer Zahl besprochen:
Geschichte in Java
- Perfekte Quadratzahlen haben perfekte Quadratwurzeln.
- Die Quadratwurzel eines geraden perfekten Quadrats ist gerade.
- Die Quadratwurzel eines ungeraden perfekten Quadrats ist ungerade.
- Die Quadratwurzel einer negativen Zahl ist a komplexe Zahl .
Tabelle der Quadratwurzel
Quadratwurzeln verschiedener Zahlen werden in der Mathematik häufig verwendet. Die folgende Tabelle gibt uns die Quadratwurzel verschiedener Zahlen, die häufig verwendet werden.
| Nummer | Quadratwurzel |
|---|---|
| 1 | √(1) = 1 |
| 2 | √(2) = 1,414 (ungefähr) |
| 3 | √(3) = 1,732 (ungefähr) |
| 4 | √(4) = 2 |
| 5 | √(5) = 2,236 (ungefähr) |
| 9 | √(9) = 3 |
| 16 | √(16) = 4 |
| 25 | √(25) = 5 |
Überprüfen Sie auch
- Quadratwurzel von 2
- Reale Nummern
- Rationale Zahlen
FAQs zur Quadratwurzel von 3
Was ist der Wert der Quadratwurzel von 3?
Der ungefähre Wert der Quadratwurzel aus 3 beträgt 1,73205.
Warum ist die Quadratwurzel aus 3 eine irrationale Zahl?
Der Wert der Quadratwurzel von 3 ist eine sich nicht wiederholende und nicht endende Dezimalzahl, also eine irrationale Zahl.
Ist die Zahl 3 ein perfektes Quadrat?
3 ist eine Primzahl und Primzahlen haben keine anderen Faktoren als 1 und sich selbst. Daher können wir sagen, dass 3 kein perfektes Quadrat ist.
Wie können wir den Wert von √3 ermitteln?
Der Wert von √3 kann mit der Methode der langen Division ermittelt werden. Da 3 kein perfektes Quadrat ist, kann der genaue Wert nie gefunden werden.
Welchen Wert hat Wurzel 2?
Wurzel 2 ist eine irrationale Zahl, daher wird ihr exakter Dezimalwert nie gefunden. Der ungefähre Wert von Wurzel 2 ist: √2 = 1,414 (ungefähr)
