Stark verbundene Komponenten (SCCs) sind ein grundlegendes Konzept in der Graphentheorie und Algorithmen. In einem gerichteten Graphen a Stark verbundene Komponente ist eine Teilmenge von Scheitelpunkten, wobei jeder Scheitelpunkt in der Teilmenge von jedem anderen Scheitelpunkt in derselben Teilmenge aus durch Überqueren der gerichteten Kanten erreichbar ist. Finden der SCCs eines Diagramms kann wichtige Einblicke in die Struktur und Konnektivität des Diagramms liefern, mit Anwendungen in verschiedenen Bereichen wie z Analyse sozialer Netzwerke, Web-Crawling und Netzwerk-Routing . In diesem Tutorial werden die Definition, Eigenschaften und effizienten Algorithmen zur Identifizierung stark verbundener Komponenten in Diagrammdatenstrukturen untersucht

Multithreading in Java

Inhaltsverzeichnis

• Was sind stark verbundene Komponenten (SCCs)?
• Warum sind stark verbundene Komponenten (SCCs) wichtig?
• Unterschied zwischen verbundenen und stark verbundenen Komponenten (SCCs)
• Warum kann die herkömmliche DFS-Methode nicht zum Auffinden stark verbundener Komponenten verwendet werden?
• Verbinden zweier stark verbundener Komponenten durch eine unidirektionale Kante
• Brute-Force-Ansatz zum Auffinden stark verbundener Komponenten
• Effizienter Ansatz zum Auffinden stark verbundener Komponenten (SCCs)
• 1. Kosarajus Algorithmus:
• 2. Tarjans Algorithmus:
• Abschluss

Was sind stark verbundene Komponenten (SCCs)?

A stark zusammenhängende Komponente Ein gerichteter Graph ist ein maximaler Teilgraph, bei dem jedes Knotenpaar für beide Seiten erreichbar ist. Das bedeutet, dass es für zwei beliebige Knoten A und B in diesem Untergraphen einen Pfad von A nach B und einen Pfad von B nach A gibt.

Zum Beispiel: Das folgende Diagramm hat zwei stark verbundene Komponenten {1,2,3,4} und {5,6,7}, da es einen Pfad von jedem Scheitelpunkt zu jedem anderen Scheitelpunkt in derselben stark verbundenen Komponente gibt.

Stark verbundene Komponente

Warum sind stark verbundene Komponenten (SCCs) wichtig?

Das Verständnis von SCCs ist für verschiedene Anwendungen von entscheidender Bedeutung, wie zum Beispiel:

• Netzwerkanalyse : Identifizieren von Clustern eng miteinander verbundener Knoten.
• Optimierung von Webcrawlern : Ermitteln von Teilen des Webdiagramms, die eng miteinander verbunden sind.
• Abhängigkeitsauflösung : In der Software das Verständnis, welche Module voneinander abhängig sind.

Unterschied zwischen verbundenen und stark verbundenen Komponenten ( SCCs)

Konnektivität in einem ungerichteter Graph bezieht sich darauf, ob zwei Scheitelpunkte voneinander erreichbar sind oder nicht. Zwei Eckpunkte gelten als verbunden, wenn zwischen ihnen ein Weg besteht. In der Zwischenzeit Stark verbunden gilt nur für gerichtete Graphen . Ein Teilgraph eines gerichteten Graphen wird als ein betrachtet Stark verbundene Komponenten (SCC) genau dann, wenn für jedes Eckpunktpaar A Und B , es gibt einen Pfad von A Zu B und ein Weg von B Zu A . Mal sehen, warum das Standard-DFS-Methode zum Auffinden verbundener Komponenten in einem Diagramm können nicht zur Bestimmung stark zusammenhängender Komponenten verwendet werden.

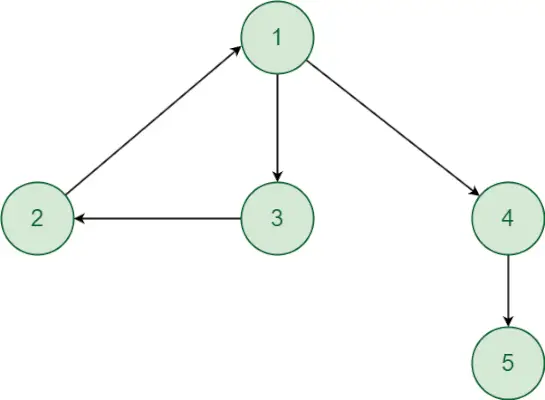
Betrachten Sie die folgende Grafik:

Python-Pfadeinstellung

Beginnen wir nun mit einem dfs Aufruf von Scheitelpunkt 1, um andere Scheitelpunkte zu besuchen.

Warum kann die herkömmliche DFS-Methode nicht verwendet werden, um die stark verbundenen Komponenten zu finden?

Alle Scheitelpunkte können von Scheitelpunkt 1 aus erreicht werden. Die Scheitelpunkte 1 und 5,6,7 können jedoch nicht in derselben stark zusammenhängenden Komponente liegen, da es keinen gerichteten Pfad von Scheitelpunkt 5,6 oder 7 zu Scheitelpunkt 1 gibt. Der Graph hat zwei stark verbundene Komponenten Zusammenhangskomponenten {1,2,3,4} und {5,6,7}. Daher kann die herkömmliche DFS-Methode nicht verwendet werden, um die stark verbundenen Komponenten zu finden.

Verbinden zweier stark verbundener Komponenten durch eine unidirektionale Kante

Zwei verschiedene verbundene Komponenten werden zu einer einzigen Komponente, wenn eine Kante zwischen einem Scheitelpunkt einer Komponente und einem Scheitelpunkt einer anderen Komponente hinzugefügt wird. Dies ist jedoch bei stark zusammenhängenden Komponenten nicht der Fall. Zwei stark verbundene Komponenten werden nicht zu einer einzigen stark verbundenen Komponente, wenn es nur eine unidirektionale Kante von einem SCC zum anderen SCC gibt.

Website wie coomeet

Brute-Force-Ansatz zum Auffinden stark verbundener Komponenten

Die einfache Methode besteht darin, für jeden Scheitelpunkt i (der nicht Teil einer starken Komponente ist) die Scheitelpunkte zu finden, die Teil der stark zusammenhängenden Komponente sein werden, die den Scheitelpunkt i enthält. Zwei Scheitelpunkte i und j befinden sich in derselben starken Zusammenhangskomponente, wenn es einen gerichteten Pfad vom Scheitelpunkt i zum Scheitelpunkt j und umgekehrt gibt.

Lassen Sie uns den Ansatz anhand des folgenden Beispiels verstehen:

• Beginnend mit Scheitelpunkt 1. Es gibt einen Pfad von Scheitelpunkt 1 zu Scheitelpunkt 2 und umgekehrt. Ebenso gibt es einen Pfad von Scheitelpunkt 1 zu Scheitelpunkt 3 und umgekehrt. Scheitelpunkt 2 und 3 befinden sich also in derselben stark verbundenen Komponente wie Scheitelpunkt 1. Es gibt zwar einen gerichteten Pfad von Scheitelpunkt 1 zu Scheitelpunkt 4 und Scheitelpunkt 5. Es gibt jedoch keinen gerichteten Pfad von Scheitelpunkt 4, 5 zu Scheitelpunkt 1, also Scheitelpunkt 4 und 5 befinden sich nicht in derselben stark verbundenen Komponente wie Scheitelpunkt 1. Somit bilden Scheitelpunkt 1, 2 und 3 eine stark verbundene Komponente.
• Für Scheitelpunkt 2 und 3 wurde die stark verbundene Komponente bereits ermittelt.
• Für Scheitelpunkt 4 gibt es einen Pfad von Scheitelpunkt 4 zu Scheitelpunkt 5, aber keinen Pfad von Scheitelpunkt 5 zu Scheitelpunkt 4. Scheitelpunkt 4 und 5 befinden sich also nicht in derselben stark verbundenen Komponente. Daher werden sowohl Vertex 4 als auch Vertex 5 Teil der Single Strongly Connected Component sein.
• Daher gibt es drei stark verbundene Komponenten {1,2,3}, {4} und {5}.

Nachfolgend finden Sie die Umsetzung des oben genannten Ansatzes:

#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, Vektor & vis) { // Wenn der aktuelle Knoten das Ziel ist, return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  }  }  }  falsch zurückgeben;  } // Um ​​festzustellen, ob es einen Pfad von der Quelle zum // Ziel gibt bool isPath(int src, int des, vector>& adj) { Vektor vis(adj.size() + 1, 0);  return dfs(src, des, adj, vis);  } // Funktion zur Rückgabe aller stark zusammenhängenden // Komponenten eines Diagramms.  Vektor> findSCC(int n, vector>& a) { // Speichert alle stark verbundenen Komponenten.  Vektor> ans;  // Speichert, ob ein Scheitelpunkt Teil eines stark // verbundenen Komponentenvektors ist is_scc(n + 1, 0);  Vektor> adj(n + 1);  für (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  für (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> Kanten{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  Vektor> ans = obj.findSCC(V, Kanten);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>

import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, Liste vis) { // Wenn der Curr-Knoten das Ziel ist, return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  }  }  }  falsch zurückgeben;  } // Um ​​festzustellen, ob es einen Pfad von der Quelle zum // Ziel gibt boolean isPath(int src, int des, List> adj) { Liste vis = new ArrayList(adj.size() + 1);  für (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> findSCC(int n, List> a) { // Speichert alle stark verbundenen Komponenten.  Aufführen> ans = new ArrayList();  // Speichert, ob ein Scheitelpunkt Teil einer stark // verbundenen Komponentenliste ist is_scc = new ArrayList(n + 1);  für (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = new ArrayList();  für (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List Kante: a) { adj.get(edge.get(0)).add(edge.get(1));  } // Alle Eckpunkte durchlaufen for (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = new ArrayList();  scc.add(i);  für (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> Kanten = new ArrayList();  Kanten.add(new ArrayList(List.of(1, 3)));  Kanten.add(new ArrayList(List.of(1, 4)));  Kanten.add(new ArrayList(List.of(2, 1)));  Kanten.add(new ArrayList(List.of(3, 2)));  Kanten.add(new ArrayList(List.of(4, 5)));  Aufführen> ans = obj.findSCC(V, Kanten);  System.out.println('Stark verbundene Komponenten sind:');  für (Liste x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Dieser Code wurde von shivamgupta310570>'> beigesteuertPython

using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, Liste vis) { // Wenn der Curr-Knoten das Ziel ist, gebe true zurück if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  }  }  }  falsch zurückgeben;  } // Um ​​festzustellen, ob es einen Pfad von der Quelle zum Ziel gibt public bool IsPath(int src, int des, List> adj) { var show = neue Liste (adj.Count + 1);  für (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> FindSCC(int n, List> a) { // Speichert alle stark verbundenen Komponenten var ans = new List>();  // Speichert, ob ein Scheitelpunkt Teil einer stark verbundenen Komponente ist. var isScc = new List (n + 1);  für (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  für (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } für (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Add(i);  für (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> Kanten = neue Liste> { neue Liste { 1, 3 }, neue Liste { 1, 4 }, neue Liste { 2, 1 }, neue Liste { 3, 2 }, neue Liste { 4, 5 } };  Aufführen> ans = obj.FindSCC(V, Kanten);  Console.WriteLine('Stark verbundene Komponenten sind:');  foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // Dieser Code wurde von shivamgupta310570>'> beigesteuertJavascript

Strongly Connected Components are: 1 2 3 4 5>

Zeitkomplexität: O(n * (n + m)), denn für jedes Eckpunktpaar prüfen wir, ob zwischen ihnen ein Pfad existiert.
Hilfsraum: O(N)

Instanziierung in Java

Effizienter Ansatz zum Auffinden stark verbundener Komponenten (SCCs)

Um SCCs in einem Diagramm zu finden, können wir Algorithmen wie verwenden Kosarajus Algorithmus oder Tarjans Algorithmus . Lassen Sie uns diese Algorithmen Schritt für Schritt erkunden.

1. Kosarajus Algorithmus :

Kosarajus Algorithmus umfasst zwei Hauptphasen:

1. Durchführen einer Tiefensuche (DFS) im Originaldiagramm :
   • Wir führen zunächst ein DFS für das ursprüngliche Diagramm durch und zeichnen die Endzeiten der Knoten auf (d. h. den Zeitpunkt, zu dem das DFS die Erkundung eines Knotens vollständig abschließt).
2. Durchführen von DFS für das transponierte Diagramm :
   • Anschließend kehren wir die Richtung aller Kanten im Diagramm um, um das transponierte Diagramm zu erstellen.
   • Als nächstes führen wir eine DFS für das transponierte Diagramm durch und berücksichtigen dabei die Knoten in absteigender Reihenfolge ihrer in der ersten Phase aufgezeichneten Endzeiten.
   • Jeder DFS-Durchlauf in dieser Phase gibt uns einen SCC.

Hier ist eine vereinfachte Version von Kosarajus Algorithmus:

1. DFS im Originaldiagramm : Zielzeiten aufzeichnen.
2. Transponieren Sie den Graphen : Alle Kanten umkehren.
3. DFS auf transponiertem Diagramm : Verarbeiten Sie Knoten in der Reihenfolge abnehmender Endzeiten, um SCCs zu finden.

2. Tarjans Algorithmus :

Tarjans Algorithmus ist effizienter, da er SCCs in einem einzigen DFS-Durchgang unter Verwendung eines Stapels und einiger zusätzlicher Buchhaltung findet:

1. DFS-Durchquerung : Verwalten Sie während des DFS einen Index für jeden Knoten und den kleinsten Index (Low-Link-Wert), der vom Knoten aus erreicht werden kann.
2. Stapel : Verfolgen Sie die Knoten, die sich derzeit im Rekursionsstapel befinden (Teil des aktuellen SCC, der untersucht wird).
3. SCCs identifizieren : Wenn der Low-Link-Wert eines Knotens seinem Index entspricht, bedeutet dies, dass wir einen SCC gefunden haben. Entfernen Sie alle Knoten vom Stapel, bis wir den aktuellen Knoten erreichen.

Hier ist eine vereinfachte Übersicht über Tarjans Algorithmus:

1. Initialisierenindex>auf 0.
2. Führen Sie für jeden nicht besuchten Knoten DFS durch.
   • Legen Sie den Index und den Low-Link-Wert des Knotens fest.
   • Schieben Sie den Knoten auf den Stapel.
   • Führen Sie für jeden benachbarten Knoten entweder DFS durch, wenn er nicht besucht wird, oder aktualisieren Sie den Low-Link-Wert, wenn er sich im Stapel befindet.
   • Wenn der Low-Link-Wert des Knotens seinem Index entspricht, werden Knoten vom Stapel entfernt, um einen SCC zu bilden.

Abschluss

Verstehen und Finden stark verbundene Komponenten in einem gerichteten Graphen ist für viele Anwendungen in der Informatik unerlässlich. Kosarajus Und Tarjans Algorithmen sind effiziente Methoden zur Identifizierung von SCCs, jeder mit seinem eigenen Ansatz und seinen eigenen Vorteilen. Wenn Sie diese Konzepte beherrschen, können Sie die Struktur und das Verhalten komplexer Netzwerke besser analysieren und optimieren.