Für jedes Objekt, das Sie sehen oder berühren können, können drei Dimensionen gemessen werden: Länge, Breite und Höhe. Es gibt bestimmte Abmessungen unseres Zuhauses, in dem wir leben. Der rechteckige Bildschirm/Monitor, den Sie betrachten, hat eine Breite und Breite seiner Länge. Für jede dreidimensionale geometrische Struktur werden Oberfläche und Volumen gemessen.
Die von der Objektoberfläche bedeckte Fläche ist die Oberfläche eines bestimmten Objekts. Die in einem Objekt verfügbare Raummenge hingegen ist das Volumen.
Inhaltsverzeichnis
- Oberfläche
- Gesamtoberfläche
- Gekrümmter Oberflächenbereich/seitlicher Oberflächenbereich
- Volumen
- Beispiele zu Oberflächen und Volumina
- FAQs zu Oberflächen- und Volumenformeln
Oberfläche
Oberfläche und Volumen können für jede dreidimensionale (3D)geometrische Form berechnet werden. Die Oberfläche einer Fläche ist der Bereich, der von der Oberfläche eines Objekts eingenommen wird. Das Volumen ist der in einem Objekt verfügbare Platz. Wir haben verschiedene Arten von Formen wie Halbkugel, Kugel, Würfel, Quader, Zylinder usw. Alle dreidimensionalen Formen haben Fläche und Volumen. Aber auch zweidimensionale Formen wie Quadrate, Rechtecke, Dreiecke, Kreise usw.
Hier können wir zweidimensional nur die Fläche messen. Die Fläche, die ein dreidimensionales Objekt mit seiner Außenfläche einnimmt, wird als Oberfläche bezeichnet. Es wird in Quadrateinheiten gemessen.
Es gibt zwei Arten von Gebieten:
- Gesamtoberfläche
- Gekrümmter Oberflächenbereich/seitlicher Oberflächenbereich
Gesamtoberfläche
Die Fläche einschließlich der Basis(n) und des gekrümmten Teils entspricht der Gesamtoberfläche. Dabei handelt es sich um die Fläche, die von der Oberfläche des Objekts umschlossen wird. Wenn die Form eine gekrümmte Basis und Oberfläche hat, ergibt die Summe der beiden Bereiche die Gesamtfläche. Die Gesamtoberfläche kann als die Gesamtfläche definiert werden, die von einem Objekt einschließlich seiner Basis und dem gekrümmten Teil bedeckt wird. Wenn ein Objekt sowohl eine Grundfläche als auch eine gekrümmte Fläche hat, entspricht die Gesamtoberfläche der Summe aus Grundfläche und gekrümmter Fläche.
- Die Gesamtoberfläche ist die Gesamtfläche, die ein Objekt einnimmt.
- Nehmen wir als Beispiel einen Quader, der 6 Flächen, 12 Kanten und 8 Eckpunkte hat.
Gesamtoberfläche = Grundfläche + gekrümmte Fläche
np.linspace
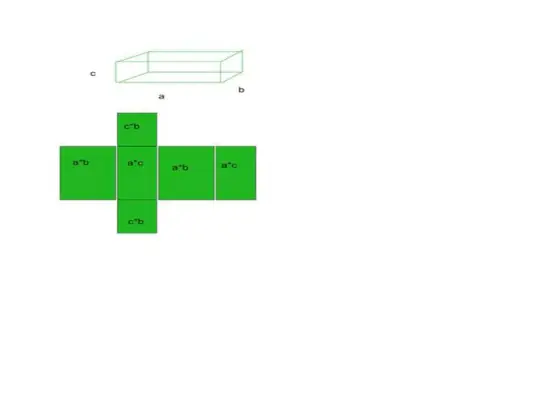
- Die Summe aller dieser insgesamt 6 Flächen ergibt unsere Gesamtoberfläche der jeweiligen Form
Beispiel:
Unten ist ein Quader dargestellt, dessen Abmessungen mit Länge = 8 cm, Breite = 4 cm und Höhe = 6 cm angegeben sind. Finden Sie die TSA eines Quaders
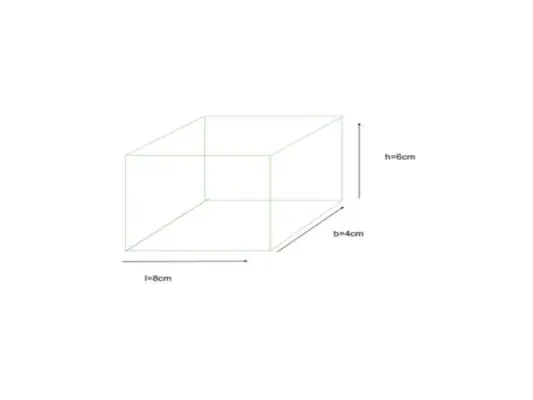
gegeben l = 8cm, b = 4cm, h = 6cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
Die TSA des Quaders beträgt 208 cm.
Gekrümmter Oberflächenbereich/seitlicher Oberflächenbereich
Der gekrümmte Oberflächenbereich mit Ausnahme seines Zentrums entspricht nur dem Bereich des gekrümmten Teils der Form(en). Bei Formen wie einem Kegel wird sie oft Mantelfläche genannt. Die seitliche Oberfläche kann als die Fläche definiert werden, die nur die gekrümmte Oberfläche eines Objekts oder die seitliche Oberfläche eines Objekts unter Ausschluss der Grundfläche eines Objekts umfasst. Die laterale Oberfläche wird auch als gekrümmte Oberfläche bezeichnet.
Die meisten Formen oder Objekte beziehen sich auf die gekrümmte Oberfläche, die Form oder der objektähnliche Zylinder bezieht sich auf die Mantelfläche. Vereinfacht ausgedrückt wird die Fläche, die für uns sichtbar ist, Mantelfläche genannt. Betrachten Sie beispielsweise den Zylinder wie in der folgenden Abbildung dargestellt.
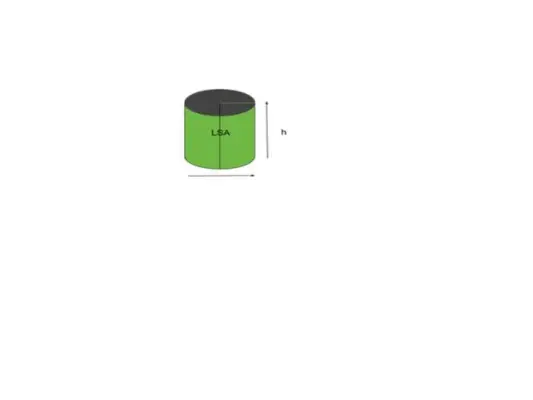
Volumen
Volumen ist die Menge an Raum in einem bestimmten 3D-Objekt. Der Gesamtraum, den ein Gegenstand oder eine Substanz einnimmt, wird als Volumen bezeichnet. Es wird in Kubikeinheiten gemessen.
Formeln für Oberfläche und Volumen
Die angegebene Tabelle enthält die Gesamtoberfläche, die gekrümmte Oberfläche/Seitenoberfläche und das Volumen verschiedener Formen.
| Name der Form | Gekrümmte Oberfläche | Gesamtoberfläche | Volumen |
|---|---|---|---|
| Quader | 2h(l + b) | 2(lb + bh + hl) | l*b*h |
| Würfel | 4a2 | 6a2 | A3 |
| Zylinder | 2πrh | 2π(r + h) | πr2H |
| Kugel | 4πr2 Stapel in Java | 4πr2 | 4/3π r3 |
| Kegel | πrl | πr(r + l) | 1/3π r2H |
| Hemisphäre | 2pr2 | 3πr2 | 2/3π r3 |
Mehr lesen:
- Oberfläche der Pyramide
- Oberfläche des Zylinders
- Oberfläche der Hemisphäre
- Oberfläche der Kugel
- Oberfläche eines Quaders
Beispiele zu Oberflächen und Volumina
Beispiel 1: 2 Würfel mit einem Volumen von je 512 cm 3 werden Ende an Ende verbunden. Finden Sie die Oberfläche des resultierenden Quaders?
Lösung:
Gegeben,
Das Volumen (V) jedes Würfels beträgt = 512 cm3
Wir können nun implizieren, dass a3= 512 cm3
∴ Seite des Würfels, also a = 8 cm
Nun beträgt die Breite und Länge des resultierenden Quaders jeweils 8 cm und die Höhe 16 cm.
Die Oberfläche des Quaders (TSA) = 2(lb + bh + lh)
Wenn wir nun die Werte eingeben, erhalten wir:
= 2(8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Daher beträgt die TSA des Quaders = 640 cm 2
Beispiel 2: Wir haben eine zylindrische Kerze mit einem Durchmesser von 14 cm und einer Länge von 2 cm. Es wird zu einer quaderförmigen Kerze mit den Maßen 7 cm x 11 cm x 1 cm geschmolzen. Wie viele quaderförmige Kerzen sind erhältlich?
Lösung:
Maße der zylindrischen Kerze:
Radius der zylindrischen Kerze = 14/2 cm = 7 cm
Höhe/Dicke = 2 cm
Volumen einer zylindrischen Kerze = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Volumen eines Quaders Kerze = 7 x 11 x 1 = 77 cm3
Daher ist die Anzahl der quaderförmigen Kerzen = Volumen der quaderförmigen Kerze/Volumen einer zylindrischen Kerze = 308/77 = 4
Somit können wir 4 quaderförmige Kerzen erhalten.
Beispiel 3: Eine Frau möchte eine kugelförmige Spielzeugkugel aus Ton bauen, deren Radius dem Radius des Armreifs entspricht, den sie trägt. Da der Armreif eine runde Form hat, möchte sie auch, dass die Fläche des Armreifs dem Volumen der Kugel entspricht. Den Radius des Armreifs herausfinden, den sie trägt?
Lösung:
Sei r der Radius des Armreifs und der Kugel,
Uns wurde gesagt, dass das Volumen der Kugel gleich der Fläche des Armreifs ist:
Somit,
πr2= 4/3 πr3
⇒ r = 3/4
Daher beträgt der Radius des Armreifs 3/4 Einheiten.
Beispiel 4: Es sei angenommen, dass die Neigungshöhe eines geraden Kreiskegels 25 cm und seine Höhe 24 cm beträgt. Finden Sie die gekrümmte Oberfläche des Kegels?
Lösung:
Die Formel für die gekrümmte Oberfläche des Kegels lautet πrl. Dabei ist r der Radius des Kegels und l die Schräghöhe des Kegels.
dynamisches Array JavaHier ist der Kegel der rechte Kreiskegel.
Der Radius des Kegels wäre also:
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Die Berechnung der gekrümmten Oberfläche erfolgt nun wie folgt:
Erforderliche Fläche = (22/7) * 7 * 25 = 550 cm2
Daher beträgt die gekrümmte Oberfläche des Kegels 550 cm 2 .
Beispiel 5: Ermitteln Sie die Mantelfläche eines Zylinders mit einem Basisradius von 6 Zoll und einer Höhe von 14 Zoll.
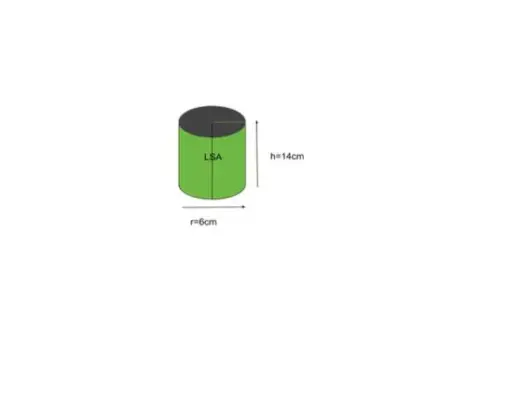
Lösung:
Gegeben sei der Radius r = 6, die Höhe h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527.787
= 528.
Die LSA des gegebenen Zylinders beträgt 528 cm .
Übungsfrage zu Oberflächen und Volumina
Verschieden Übungsfragen zu Flächen und Volumen Formeln sind:
Q1. Ermitteln Sie die Oberfläche eines Würfels mit einer Seitenlänge von 5 Zentimetern.
Q2. Berechnen Sie das Volumen einer Kugel mit einem Radius von 3 Metern.
Q3. Bestimmen Sie die Gesamtoberfläche eines Zylinders mit einem Radius von 4 Zentimetern und einer Höhe von 8 Zentimetern.
Q4. Ermitteln Sie das Volumen eines Kegels mit einem Radius von 6 Zoll und einer Höhe von 10 Zoll.
F5. Berechnen Sie die Oberfläche eines rechteckigen Prismas mit einer Länge von 7 Metern, einer Breite von 4 Metern und einer Höhe von 6 Metern.
FAQs zu Oberflächen- und Volumenformeln
Wie lauten die Formeln für Oberfläche und Volumen?
Im obigen Artikel werden verschiedene Oberflächen- und Volumenformeln hinzugefügt.
Wie lautet die Formel für das Oberflächenvolumen der Klasse 10?
Die Formel für Oberflächen- und Volumenklasse 10 enthält:
| Name der Form | Gekrümmte Oberfläche | Gesamtoberfläche | Volumen |
|---|---|---|---|
| Quader Was ist ein Stack in Java? | 2h(l + b) | 2(lb + bh + hl) | l × b × h |
| Würfel | 4a2 | 6a2 | A3 |
| Zylinder | 2πrh | 2π(r + h) | πr2H |
| Kugel | 4πr2 | 4πr2 | 4/3π r3 |
| Kegel | πrl | πr(r + l) | 1/3π r2H |
| Hemisphäre | 2pr2 | 3πr2 | 2/3π r3 |
Wie lautet die Formel für Quader in Oberfläche und Volumen?
- Oberfläche des Quaders = 2(lb + bh + hl)
- Volumen von Cubiod = l × b × h
Was ist Oberfläche und Volumen?
Die Oberfläche ist die Fläche aller Oberflächen eines Festkörpers und sein Volumen ist der vom Sloid eingenommene Raum.
