Die Trigonometrie ist ein wichtiger Zweig der Mathematik, der sich mit der Beziehung zwischen Winkeln und Längen der Seiten eines rechtwinkligen Dreiecks beschäftigt. Die sechs trigonometrischen Verhältnisse oder Funktionen sind Sinus, Kosinus, Tangens, Kosekans und Sekante, und ein trigonometrisches Verhältnis ist ein Verhältnis zwischen den Seiten eines rechtwinkligen Dreiecks. Sinus-, Kosinus- und Tangensfunktionen sind drei wichtige trigonometrische Funktionen, da die anderen drei, d. h. Kosekans-, Sekanten- und Kotangensfunktionen, die reziproken Funktionen von Sinus-, Kosinus- bzw. Tangensfunktionen sind.
- sin θ = Opposite side/Hypotenuse
- cos θ = Ankathete/Hypotenuse
- tan θ = Gegenseite/Angrenzende Seite
- cosec θ = Hypotenuse/Gegenkathete
- sec θ = Hypotenuse/angrenzende Seite
- cot θ = Angrenzende Seite/Gegenseite
Die Tangentenfunktion ist eine der 6 trigonometrischen Funktionen, die in verwendet werden Trigonometrieformeln .
Inhaltsverzeichnis
Tangentenformel
Der Tangens eines Winkels in einem rechtwinkligen Dreieck ist das Verhältnis der Länge der gegenüberliegenden Seite zur Länge der benachbarten Seite zum gegebenen Winkel. Wir schreiben eine Tangensfunktion als tan. Betrachten wir ein rechtwinkliges Dreieck XYZ und einer seiner spitzen Winkel ist θ. Eine gegenüberliegende Seite ist die Seite, die dem Winkel θ gegenüberliegt, und die benachbarte Seite ist die Seite, die dem Winkel θ benachbart ist.
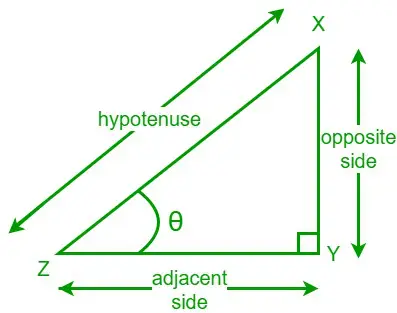
Die Tangensformel für den gegebenen Winkel θ lautet nun:
tan θ = Gegenseite/Angrenzende Seite
Einige grundlegende Tangentenformeln
Tangentenfunktion in Quadranten
Die Tangensfunktion ist im ersten und dritten Quadranten positiv und im zweiten und vierten Quadranten negativ.
- tan (2π + θ) = tan θ (1stQuadrant)
- tan (π – θ) = – tan θ (2ndQuadrant)
- tan (π + θ) = tan θ (3rdQuadrant)
- tan (2π – θ) = – tan θ (4ThQuadrant)
Tangentenfunktion als negative Funktion
Die Tangensfunktion ist eine negative Funktion, da der Tangens eines negativen Winkels das Negative eines tangentialen positiven Winkels ist.
tan (-θ) = – tan θ
Tangensfunktion im Sinne der Sinus- und Kosinusfunktion
Die Tangentenfunktion in Form von Sinus- und Kosinusfunktionen kann wie folgt geschrieben werden:
tan θ = sin θ/cos θ
Wir wissen, dass tan θ = Gegenseite/Angrenzende Seite ist
Teilen Sie nun Zähler und Nenner durch die Hypotenuse
tan θ = (Gegenseite/Hypotenuse)/(Angrenzende Seite/Hypotenuse)
Wir wissen, dass sin θ = gegenüberliegende Seite/Hypotenuse
cos θ = Ankathete/Hypotenuse
Daher ist tan θ = sin θ/cos θ
Tangentenfunktion im Sinne einer Sinusfunktion
Die Tangentenfunktion im Sinne der Sinusfunktion kann wie folgt geschrieben werden:
tan θ = sin θ/(√1 – sin 2 ich)
Wir wissen das,
tan θ = sin θ/cos θ
np.sum
Aus den pythagoreischen Identitäten haben wir:
ohne2θ + cos2θ = 1
cos2θ = 1 – Sünde2ich
cos θ = √(1 – sin2ich)
Daher ist tan θ = sin θ/(√1 – sin2ich)
Tangensfunktion im Sinne der Kosinusfunktion
Die Tangensfunktion im Sinne der Kosinusfunktion kann wie folgt geschrieben werden:
tan θ = (√1 -cos 2 i)/weil ich
Wir wissen das,
tan θ = sin θ/cos θ
Aus den pythagoreischen Identitäten haben wir:
ohne2θ + cos2θ = 1
ohne2θ = 1 – cos2ich
sin θ = √(1 – cos2ich)
Daher ist tan θ = (√1 – cos2i)/weil ich
Tangensfunktion im Sinne der Kotangensfunktion
Die Tangentenfunktion im Sinne der Kotangensfunktion kann wie folgt geschrieben werden:
tan θ = 1/cot θ
oder
tan θ = cot (90° – θ) (oder) cot (π/2 – θ)
Tangensfunktion im Sinne der Kosekansfunktion
Die Tangensfunktion im Sinne der Kosekantenfunktion kann geschrieben werden als:
tan θ = 1/√(cosec 2 ich – 1)
Aus den pythagoreischen Identitäten haben wir:
cosec2θ – Kinderbett2θ = 1
Kinderbett2θ = cosec2ich – 1
cot θ = √(cosec2ich – 1)
Wir wissen das,
tan θ = 1/cot θ
Daher ist tan θ = 1/√(cosec2ich – 1)
Tangentenfunktion im Sinne einer Sekantenfunktion
Die Tangentenfunktion im Sinne der Sekantenfunktion kann geschrieben werden als:
tan θ = √sec 2 ich – 1
Aus den pythagoreischen Identitäten haben wir:
Sek2θ – also2θ = 1
tan θ = sek2ich – 1
Daher ist tan θ = √(sec2ich – 1)
Tangentenfunktion im Hinblick auf den Doppelwinkel
Die Tangensfunktion für einen Doppelwinkel lautet:
tan 2θ = (2 tan θ)/(1 – tan 2 ich)
Tangentenfunktion im Sinne des Dreifachwinkels
Die Tangensfunktion für einen Dreifachwinkel lautet:
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 tan 2 ich)
Tangentenfunktion als Halbwinkel
Die Tangensfunktion für einen halben Winkel lautet:
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / (sin θ)
Tangentenfunktion im Sinne der Addition und Subtraktion zweier Winkel
Summen- und Differenzformeln für eine Tangensfunktion lauten:
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
Trigonometrische Verhältnistabelle
| Winkel (in Grad) | Winkel (im Bogenmaß) | Sünde ich | cos θ | tan θ = sin θ/cos θ | cosec θ | Sek. θ | Kinderbett i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Nicht definiert | 1 | Nicht definiert |
| 30° | S. 6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | S./4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | S./3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 String-Splitting C++ | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = undefiniert | 1 | Nicht definiert | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Nicht definiert | -1 | Nicht definiert |
Gelöstes Beispiel für Tangentenformeln
Beispiel 1: Ermitteln Sie den Wert von tan θ, wenn sin θ = 2/5 und θ der erste Quadrantenwinkel ist.
Lösung:
Gegeben,
- Sünde θ = 2/5
Aus den pythagoräischen Identitäten, die wir haben,
ohne2θ + cos2θ = 1
cos2θ = 1 – Sünde2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Da θ der erste Quadrantenwinkel ist, ist cos θ positiv.
cos θ = √21/5
Wir wissen das,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21 /21
Der Wert von tan θ beträgt also (2√21) /(21), wenn sin θ = 2/5 und θ im ersten Quadranten liegt.
Beispiel 2: Ermitteln Sie den Wert von tan x, wenn sec x = 13/12 und x der vierte Quadrantenwinkel ist.
Lösung:
Gegeben sei Sek. x = 13/12
Aus den pythagoreischen Identitäten haben wir:
Sek2x – also2x = 1
Also2x = Sek2x – 1= (13/12)2- 1
Also2x = (169/144) – 1= 25/144
tan x = ± 5/12
Da x der vierte Quadrantenwinkel ist, ist tan x negativ.
tan x = – 5/12
Somit, tan x = – 5/12
Beispiel 3: Wenn tan X = 2/3 und tan Y = 1/2, welchen Wert hat dann tan (X + Y)?
Lösung:
Gegeben,
tan X = 2/3 und tan Y = 1/2
Wir wissen das,
tan (X + Y) = (tan X + tan Y)/(1 – tan X tan Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Somit, tan(X + Y) = 7/4
Beispiel 4: Berechnen Sie die Tangensfunktion, wenn die benachbarten und gegenüberliegenden Seiten eines rechtwinkligen Dreiecks jeweils 4 cm und 7 cm betragen.
Lösung:
Gegeben,
Angrenzende Seite = 4 cm
Gegenseite = 7 cm
Wir wissen das,
tan θ = Gegenseite/Angrenzende Seite
tan θ = 7/4 = 1,75
Somit, tan θ = 1,75
Beispiel 5: Ein Mann blickt auf einen Uhrturm im 60°-Winkel zur Turmspitze, deren Höhe 100 m beträgt. Wie groß ist der Abstand zwischen dem Mann und dem Fuß des Turms?
Lösung:
Gegeben,
Fehler: Hauptklasse konnte nicht gefunden oder geladen werdenHöhe des Turms = 100 m und θ = 60°
Sei der Abstand zwischen Mann und Turmfuß = d
Wir haben,
tan θ = Gegenseite/Angrenzende Seite
tan 60° = 100/d
√3 = 100/d [Da also 60° = √3]
d = 100/√3
Daher beträgt der Abstand zwischen dem Mann und dem Fuß des Turms 100/√3
Beispiel 6: Ermitteln Sie den Wert von tan θ, wenn sin θ = 7/25 und sec θ = 25/24.
Lösung:
Gegeben,
Sünde θ = 7/25
Sek. θ = 25/24
Wir wissen das,
Sek. θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Wir haben,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
Somit, tan θ = 7/24
Beispiel 7: Ermitteln Sie den Wert von tan θ, wenn cosec θ = 5/3 und θ der erste Quadrantenwinkel ist.
Lösung:
Gegeben ist cosec θ = 5/3
Aus den pythagoreischen Identitäten haben wir:
string.format Javacosec2θ – Kinderbett2θ = 1
Kinderbett2θ = cosec2ich – 1
Kinderbett θ = (5/3)2– 1 = (25/9) – 1 = 16/9
Kinderbett θ = ±√16/9 = ± 4/3
Da θ der erste Quadrantenwinkel ist, sind sowohl die Kotangens- als auch die Tangensfunktion positiv.
Kinderbett θ = 4/3
Wir wissen das,
cot θ = 1/tan θ
4/3 = 1/tanθ
tan θ = 3/4
Somit, tan θ = 3/4
Beispiel 8: Finden Sie tan 3θ, wenn sin θ = 3/7 und θ der erste Quadrantenwinkel ist.
Lösung :
Gegeben sei sin θ = 12/13
Aus den pythagoräischen Identitäten, die wir haben,
ohne2θ + cos2θ = 1
cos2θ = 1 – Sünde2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Da θ der erste Quadrantenwinkel ist, ist cos θ positiv.
cos θ = 5/13
Wir wissen das,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Daher ist tan θ = 12/5
Nun, wir wissen, dass
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

