Trapez in Mathematik: Ein Trapez ist ein Polygon mit vier Seiten, also ein Viereck. Trapez stammt vom griechischen Wort trapeze ab, was Tisch bedeutet. Es handelt sich um ein komplexes Viereck. Ein Trapez ist ein spezielles Viereck mit nur einem Paar paralleler Seiten. Ein Trapez ist eine zweidimensionale Form, die wie ein Tisch aussieht.
Ein Trapez hat vier Seiten und vier Eckpunkte. Wir sehen die Trapezform in unserem täglichen Leben und sie ist eine der häufigsten Formen. In diesem Artikel erfahren wir mehr darüber Was ist Trapez in der Mathematik? Seine Eigenschaften, Formeln, Beispiele und Arten von Trapezen sowie einige gelöste Beispiele dafür.
Inhaltsverzeichnis
- Was ist ein Trapez in der Mathematik?
- Arten von Trapezen
- Unregelmäßiges Trapez
- Eigenschaften von Trapez
- Trapezformel
- Fläche der Trapezformel
- Umfang der Trapezformel
- Unterschied zwischen Trapez und Trapez
- Winkel des Trapezes
- Diagonale des Trapezes
- Beispiele für Trapeze
Was ist ein Trapez in der Mathematik?
Ein Trapez ist ein geschlossen geformtes zweidimensionales Viereck mit zwei parallelen gegenüberliegenden Seiten. Die parallelen Seiten eines Trapezes werden Basen genannt und die nicht parallelen Seiten eines Trapezes werden Beine genannt. Das Trapez hat vier Seiten und vier Ecken. A Parallelogramm wird auch Trapez mit zwei parallelen Seiten genannt.
Trapez-Definition
Ein Trapez ist ein Viereck (ein vierseitiges Polygon) mit mindestens einem Paar paralleler Seiten. Diese parallelen Seiten werden als Basen des Trapezes bezeichnet, und die anderen beiden Seiten werden als Beine bezeichnet, die nicht unbedingt parallel sind.
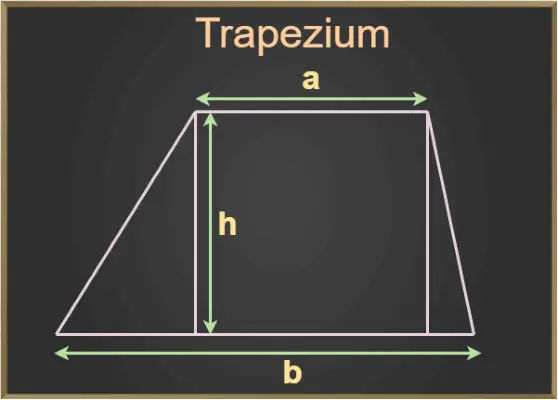
In der obigen Abbildung sind a und b die Basen des Trapezes und h die Höhe des Trapezes.
Trapezform
Trapez ist ein Viereck d.h. Polygon mit vier Seiten. Ein Trapez hat vier Seiten mit zwei gegenüberliegenden Seiten, die parallel zueinander sind. Die Trapezform ist sehr verbreitet und wir sehen in unserem täglichen Leben verschiedene Dinge, die dem Trapez ähneln. Einige von uns beobachtete reale Beispiele für Trapeze sind trapezförmige Tische, Fliesen, Gemälde und andere.
Arten von Trapezen
Basierend auf den Seiten und den Winkeln gibt es drei Arten von Trapezen:
- Scalene-Trapez
- Gleichschenkliges Trapez
- Rechtes Trapez

Gleichschenkliges Trapez
Das Trapez, dessen Schenkel gleich lang sind, wird als gleichschenkliges Trapez bezeichnet, d. h. bei einem gleichschenkligen Trapez sind die beiden nicht parallelen Seiten gleich.
Scalene-Trapez
Ein Trapez, bei dem alle Seiten ungleich sind, wird Skalentrapez genannt. In einem ungleichseitigen Trapez sind keine zwei Winkel gleich.
Hacking-Verarbeitung
Rechtes Trapez
Ein Trapez, bei dem ein rechtwinkliges Paar nebeneinander liegt, wird als rechtes Trapez bezeichnet.
Unregelmäßiges Trapez
Ein Trapez hat ein Paar paralleler Seiten und die anderen beiden Seiten sind nicht parallel. Bei einem regelmäßigen Trapez sind die beiden anderen nichtparallelen Seiten gleich, bei einem unregelmäßigen Trapez hingegen sind die beiden nichtparallelen gegenüberliegenden Seiten ungleich.
Eigenschaften von Trapez
Es gibt verschiedene Eigenschaften von Trapez, von denen einige wie folgt sind:
- Parallele Seiten: Ein Trapez hat zwei parallele Seiten, die Basen genannt werden. Beispiel: Die Seiten AB und CD sind parallel zueinander, wie in der Abbildung dargestellt.
- Nichtparallele Seiten: Nicht parallele Seiten eines Trapezes werden Beine genannt und die Beine eines Trapezes sind nicht gleich lang. Beispiel: Die Seiten AD und BC sind nicht parallele Seiten des Trapezes.
- Höhe oder Höhe: Der senkrechte Abstand zwischen den Basen wird als Höhe oder Höhe des Trapezes bezeichnet. Im obigen Diagramm ist h die Höhe des Trapezes.
- Summe der Winkel
- Benachbarte Innenwinkel in einem Trapez ergeben zusammen 180°. Beispiel: Es gibt zwei Paare von Innenwinkeln. Ein Paar ist ∠ A und ∠ D, während das andere Paar ∠ B und ∠ C ist. Die Summe jedes Paares von Innenwinkeln beträgt 180°.
- Die Summe aller Innenwinkel in einem Trapez beträgt immer 360°. Beispiel : In der Abbildung beträgt ∠A+∠D 180° und ∠B+∠C 180°. Daher ist ∠A+∠D +∠B+∠C = 360°.
- Median: Die Mediane eines Trapezes ist das Liniensegment, das die Mittelpunkte der Beine verbindet. Der Median verläuft parallel zu den Basen und seine Länge ist der Durchschnitt der Längen der Basen.
- Das Trapez hat genau ein Paar gegenüberliegender Seiten, die parallel sind.
Trapezformel
Wichtige Formeln eines Trapezes sind:
- Bereich des Trapezes = ½ (Summe paralleler Seiten) × (Abstand zwischen parallelen Seiten)
- Umfang des Trapezes = Summe aller vier Seiten
Fläche der Trapezformel
Das Trapez hat zwei parallele Seiten a bzw. b und seine Höhe beträgt h.
Jetzt kann die Fläche des Trapezes berechnet werden, indem der Durchschnitt der Basen ermittelt und das Ergebnis mit der Höhe multipliziert wird. Somit,
Bereich des Trapezes = ((a +b)/2) × h
Wo,
- A Und B sind Basen des Trapezes
- H ist Höhe
Fläche des gleichschenkligen Trapezes
Seien a und b die Länge paralleler Seiten eines Trapezes ABCD, wobei a und b die Basen des Trapezes sind und a>b.
Da es sich nun um ein gleichschenkliges Trapez handelt, ist c die Länge der beiden nichtparallelen Seiten und h die Höhe des Trapezes.
Nun ist AB = a, CD = b, BC = AD = c
In Rechtwinkliges Dreieck , AED
Länge der Senkrechten, h = √(c 2 – (ab) 2 ) [verwenden Satz des Pythagoras ]….(1)
Jetzt,
Fläche = ½ × Summe paralleler Seiten × Höhe des Trapezes
Fläche = ½ × (a+b) × h
Verwendung von Gleichung (1)
Fläche des gleichschenkligen Trapezes = 1/2 × [√(c 2 – (ab) 2 ) (a+b)]
Umfang der Trapezformel
Der Umfang eines Trapezes ergibt sich aus der Summe aller seiner Seiten. Somit,
Umfang des Trapezes = AB + BC + CD + AD
Wo, AB, BC, CD Und ANZEIGE sind Seiten des Trapezes
Umfang des gleichschenkligen Trapezes
Wenn in einem gleichschenkligen Trapez a und b die Längen paralleler Seiten, d. h. der Basen, sind und c die Länge zweier gleicher nichtparalleler Seiten ist, dann ist der Umfang gegeben durch:
Umfang = a + b + 2c
Wo,
- A , B sind Basen des Trapezes
- C ist die gleiche Seite des Trapezes
Unterschied zwischen Trapez und Trapez
Im Allgemeinen sind sowohl Trapezium als auch Trapezoid gleich, der Unterschied liegt jedoch in ihrem Herkunftsland.
Python-sortiertes Tupel
- Trapez ist britischen Ursprungs, es ist ein vierseitiges Polygon und eine zweidimensionale Figur, es hat genau ein Paar einander gegenüberliegender paralleler Seiten. In Indien orientieren wir uns am britischen Englisch, daher wird das Wort Trapezium verwendet.
- Trapez ist amerikanischen Ursprungs, es ist ebenfalls ein vierseitiges Polygon mit einem Paar einander gegenüberliegender paralleler Seiten. Parallele Seiten sind die Basen und zwei weitere nicht parallele Seiten werden als Beine des Trapezes bezeichnet.
Winkel des Trapezes
Das Trapez ist ein Viereck und die Summe aller Winkel eines Vierecks beträgt 360 Grad. Die Summe aller Innenwinkel des Trapezes beträgt also 360 Grad.
Für jedes regelmäßige Trapez, d. h. das Trapez, bei dem die nicht parallelen Seiten gleich den angrenzenden Winkeln sind, die zwischen der parallelen Linie und der nicht parallelen Linie gebildet werden, ist gleich. Somit ist die Summe dieser beiden Winkel ergänzend.
Nehmen wir ein Beispiel, um dieses Konzept für ein gleichschenkliges Trapez ABCD zu untermauern. Wenn AB parallel zu CD und AD gleich CD ist, dann wissen wir, dass ∠A = ∠B und ∠C = ∠D.
∠A + ∠B + ∠C + ∠D = 360°
Hier gilt: ∠A = ∠B und ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Ebenso ist (∠B + ∠D) = 180°
Diagonale des Trapezes
Das Trapez ist eine Sonderform des Vierecks; Daher hat auch das Trapez zwei Diagonalen. Im Gegensatz zu einigen anderen Vierecken wie Rechtecken oder Parallelogrammen sind die Diagonalen eines Trapezes nicht gleich lang. Diagonalen eines Trapezes haben nicht die gleiche Länge und die Länge der Diagonalen hängt von der Länge der Basen und den Winkeln des Trapezes ab.
Beispiel: Für ein gleichschenkliges Trapez ABCD beträgt der Basiswinkel ∠A 80°, dann ermitteln Sie den anderen Winkel ∠C.
Wir wissen, dass für ein gleichschenkliges Trapez ABCD
(∠A + ∠C) = 180°
Gegeben sei ∠A = 80°
Nun, 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100°
Somit beträgt der erforderliche Winkel ∠C 100°
Trapezformeln – Fläche und Umfang des Trapezes
Formeln zum Thema Trapez sind in der folgenden Tabelle zusammengefasst:
| Eigentum | Formel |
|---|---|
| Bereich | 1/2 × ( A + B ) × H |
| Fläche (gleichschenkliges Trapez) | 1/2 × [√(c2– (ab)2) (a+b)] Letztes Commit rückgängig machen |
| Umfang | A + B + C + D |
| Umfang (gleichschenkliges Trapez) | A + B + 2 C |
| Median | (A + b)/2 |
Die Leute lesen auch:
- Rhombus
- Dreieck
- Was ist die Formel, um die Fläche eines Trapezes zu ermitteln?
Beispiele für Trapeze
Beispiel 1: Finden Sie die vierte Seite des Trapezes, wenn die anderen drei Seiten 8 cm, 12 cm und 16 cm groß sind und der Umfang 40 cm beträgt.
Lösung:
Der Umfang wird als Summe aller seiner Seiten angegeben. Die Länge der Unbekannten sei „x“ Einheiten.
Umfang = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
Somit beträgt die Länge der unbekannten Seite 4 cm
Beispiel 2: Ein Trapez hat parallele Seiten mit einer Länge von 15 cm und 11 cm und nichtparallele Seiten mit einer Länge von jeweils 5 cm. Berechnen Sie den Umfang des Trapez.
Lösung:
Es handelt sich um ein gleichschenkliges Trapez, da klar erwähnt ist, dass nicht parallele Seiten mit einer Länge von jeweils 5 cm gleich sind.
Laut Isosceles Trapezium wird es als Isosceles Trapezium bezeichnet, wenn zwei nicht parallele Seiten des Trapezes gleich lang sind.
Gegeben,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Umfang = a + b + 2c
P = 15 + 11 + 2(5)
P = 15 + 11 + 10
P = 36 cm
Beispiel 3: Finden Sie den Umfang eines Trapezes, dessen Seiten 12 cm, 14 cm, 16 cm und 18 cm betragen.
Lösung:
P = Summe aller Seiten
P = 12 + 14 + 16 + 18
Java konvertiert int in einen StringP = 60 cm
Daher beträgt der Umfang des Trapezes 60 cm
Beispiel 4: Finden Sie die Fläche eines Trapezes, dessen Summe paralleler Seiten 60 cm und dessen Höhe 10 cm beträgt.
Lösung:
Gegeben,
- Summe der parallelen Seiten 60 cm
- Höhe, h = 10 cm
Fläche des Trapezes, A = 1/2 × Summe paralleler Seiten × Abstand zwischen parallelen Seiten
Gegebene Werte ersetzen,
A =1/2×60×10
A = 30×10
A = 300 cm2
Daher beträgt die Fläche des Trapezes 300 cm2
Übungsaufgaben zum Trapez in Mathematik
1. Ermitteln Sie die Fläche eines Trapezes mit einer Grundfläche von 10 cm und 15 cm und einer Höhe von 6 cm.
2. Ein Trapez hat eine Fläche von 54 Quadratmetern. Wenn einer der Sockel 12 Meter lang und die Höhe 6 Meter ist, ermitteln Sie die Länge des anderen Sockels.
3. Berechnen Sie den Umfang eines Trapezes mit einer Grundfläche von 8 cm und 14 cm und nicht parallelen Seiten von 5 cm und 7 cm.
4. Bestimmen Sie die Länge des Mittelsegments in einem Trapez, dessen Basis 18 cm und 30 cm misst.
5. Bei einem gleichschenkligen Trapez betragen die Winkel an einer Basis jeweils 45 Grad. Finden Sie die Winkelmaße an der anderen Basis. Angenommen, das Trapez ist kein rechtes Trapez.
Zusammenfassung – Trapez in der Mathematik
Ein Trapez ist ein vierseitiges Polygon oder Viereck, das dadurch gekennzeichnet ist, dass es ein Paar paralleler Seiten, sogenannte Basen, hat, während die anderen beiden Seiten, sogenannte Beine, nicht parallel sind. Das in Alltagsgegenständen wie Tischen übliche Trapez zeichnet sich durch seine geometrischen Eigenschaften aus: Es hat eine Höhe, die dem senkrechten Abstand zwischen den Basen entspricht, und einen Mittelwert, der die Mittelpunkte der nicht parallelen Seiten verbindet und parallel zu den Basen verläuft.
Die Fläche eines Trapezes wird durch Mittelung der Grundlängen und Multiplikation mit der Höhe berechnet, während sein Umfang die Summe aller seiner Seiten ist. Mit unterschiedlichen Klassifizierungen wie Skalenen, Gleichschenkligen und Rechtstrapezen, die jeweils einzigartige Seiten- und Winkeleigenschaften aufweisen, sind Trapeze sowohl für praktische Anwendungen als auch für die geometrische Theorie von grundlegender Bedeutung.
FAQs zum Thema Trapez in Mathematik
Was ist Trapezform?
Trapez ist ein Viereck, bei dem ein Linienpaar immer parallel ist. Es ähnelt der Form eines Tisches. Sein Name leitet sich vom griechischen Wort trapeze ab, was Tisch bedeutet.
Wie viele Arten von Trapezen?
Es gibt zwei Arten von Trapezen:
Algorithmus für die binäre Suche
- Regelmäßiges Trapez: In dem das andere Linienpaar gleich ist.
- Unregelmäßiges Trapez: In dem das andere Linienpaar nicht gleich ist.
Wie viele parallele Seiten hat ein Trapez?
Wir wissen, dass das Trapez ein Viereck mit einem Paar paralleler Seiten ist. Ein Trapez hat also ein Paar paralleler Linien (Seiten).
Kann ein Trapez als Viereck betrachtet werden?
A hat vier Seiten, vier Eckpunkte und vier Winkel. Daher kann es als Viereck betrachtet werden; die Summe aller vier Innenwinkel eines Trapezes beträgt 360 Grad.
Kann man ein Quadrat als Trapez bezeichnen?
Ein Trapez ist ein Viereck mit nur einem Paar paralleler Seiten und die anderen beiden Seiten sind nicht parallel. Da ein Quadrat jedoch zwei Paare paralleler Seiten hat, kann es nicht als Trapez betrachtet werden.
Sind die Diagonalen eines Trapezes immer gleich?
Die Diagonalen eines Trapezes sind möglicherweise nicht gleich. Bei einem regelmäßigen Polygon sind die Diagonalen gleich, bei einem unregelmäßigen Polygon ist dies jedoch nicht der Fall.
Welche Eigenschaften hat ein Trapez?
5 Eigenschaften eines Trapezes sind:
- Beim Trapez sind die Basen parallel zueinander.
- Ein Trapez hat zusätzliche angrenzende Winkel.
- Nur ein Paar gegenüberliegender Seiten ist parallel.
- Die Summe aller Innenwinkel in einem Trapez beträgt immer 360°.
- Die Linie, die den Mittelpunkt nicht paralleler Seiten verbindet, ist immer parallel zu den Basen.
