Volumen einer Kugel ist die Flüssigkeitsmenge, die eine Kugel aufnehmen kann. Die Formel für das Kugelvolumen wird mit 4/3πr angegeben³. Es ist der Raum, den eine Kugel im dreidimensionalen Raum einnimmt. Es wird in Einheiten gemessen³d.h. m³, cm³usw. Eine Kugel ist ein dreidimensionaler fester Gegenstand mit einer runden geometrischen Form.

Das Volumen der Kugel ist der Gesamtraum, der von der Kugeloberfläche eingenommen wird, und ist proportional zur dritten Potenz des Kugelradius. In diesem Artikel lernen wir das Kugelvolumen, die Formel für das Kugelvolumen, Beispiele für die Formel für das Kugelvolumen und andere im Detail kennen.

• Was ist das Volumen einer Kugel?
• Volumen der Kugelformel
• Volumen einer festen Kugel
• Volumen einer Hohlkugel
• Volumen der Ableitung der Kugelformel
• Wie berechnet man das Kugelvolumen?

Was ist das Volumen einer Kugel?

Das Volumen einer Kugel ist der Raum, den sie darin einnimmt. Die Kugel ist eine dreidimensionale, runde, feste Form, bei der alle Punkte auf ihrer Oberfläche den gleichen Abstand von ihrem Mittelpunkt haben. Der feste Abstand ist der Radius der Kugel und der feste Punkt ist der Mittelpunkt der Kugel. Wir werden eine Formveränderung bemerken, wenn der Kreis gedreht wird. Durch die Drehung des als Kreis bezeichneten zweidimensionalen Objekts entsteht die dreidimensionale Form einer Kugel.

Erfahren Sie mehr,

• Kugel
• Oberfläche der Kugel

Volumen einer Kugeldefinition

Das Volumen einer Kugel ist die Gesamtmasse, die von der Kugeloberfläche umschlossen wird. Es ist der dreidimensionale Raum innerhalb der Kugel. Es kommt auf den Radius der Kugel an. Das unten hinzugefügte Bild zeigt eine Kugel mit dem Radius r und ihrem Volumen.

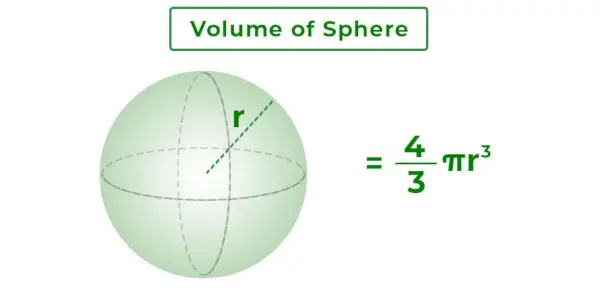
Volumen der Kugelformel

Die Formel „Volumen der Kugel“ ist die Formel, die verwendet wird, um das Volumen der Kugel zu ermitteln, wenn ihr Radius angegeben ist. Die Formel für das Kugelvolumen für die Kugel mit dem Radius R wird unten hinzugefügt:

Formel für das Kugelvolumen = 4/3πr ³

Wo,

• R ist der Radius einer Kugel
• Pi ist eine Konstante und ihr Wert ist 22/7

Eine Kugel wird im Allgemeinen in zwei Kategorien eingeteilt:

• Volumen einer festen Kugel
• Volumen der Hohlkugel

Lassen Sie uns mehr über sie im Detail erfahren.

Volumen einer festen Kugel

Eine feste Kugel ist eine Kugel, die bis ins Innere vollständig gefüllt ist. d. h. es hat Masse bis zu seinem Kern und seine Formel für das Volumen, wenn sein Radius r ist, lautet:

Volumen einer festen Kugel (V) = (4/3)πr ³

Volumen einer Hohlkugel

Für eine Hohlkugel ist ihr Innenraum leer und angenommen, ihr Außenradius ist leer R und sein Innenradius ist R, dann wird sein Volumen mit der Formel berechnet:

Volumen der Hohlkugel = (4/3)π(R ³ - R ³ )

Volumen der Ableitung der Kugelformel

Die Formel für das Kugelvolumen kann mit den folgenden Methoden abgeleitet werden:

• Integration nutzen
• Verwendung der archimedischen Beziehung zwischen Zylinder, Kegel und Kugel

Lassen Sie uns diese Methoden wie folgt im Detail besprechen:

Kugelvolumen mittels Integration

Mit dem Integrationsansatz können wir einfach das Volumen einer Kugel berechnen.

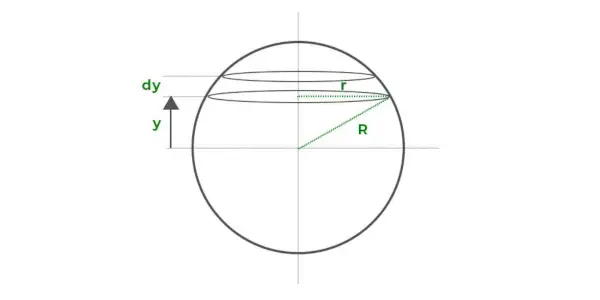
Angenommen, das Volumen der Kugel besteht aus einer Reihe dünner kreisförmiger Scheiben, die übereinander gestapelt sind, wie im Diagramm oben dargestellt. Jede dünne Scheibe hat einen Radius r und eine Dicke dy, die dem y-Abstand von der x-Achse entspricht.

Das Volumen einer Disc sei dV. Der Wert von dV ist gegeben durch:

dV = (πr²) Du

Somit ist dV = π (R²- Und²) Du

Das Gesamtvolumen der Kugel ist die Summe der Volumina aller dieser kleinen Scheiben. Der erforderliche Wert kann durch Integration des Ausdrucks von limit -R bis R erhalten werden.

Das Volumen der Kugel wird also zu

V =int_{y=-R}^{y=R} dV

⇒ V =int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V =pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V =pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V =pi left[2R^3-frac{2R^3}{3} ight]

⇒ V =frac{4}{3}pi R^3

Daraus ergibt sich die Formel für das Kugelvolumen.

Volumen der Kugel unter Verwendung der Archimedes-Beziehungen

Wie Archimedes bereits bewiesen hat, stehen ihre Volumina im Verhältnis 1:2:3, wenn ein Kegel, eine Kugel und ein Zylinder den gleichen Radius r und die gleiche Höhe haben.

Deshalb können wir sagen:

Volumen des Zylinders = Volumen des Kegels + Volumen der Kugel

Somit ist das Kugelvolumen = das Zylindervolumen – das Kegelvolumen

Wie wir wissen, ist das Zylindervolumen = πr²h und Kegelvolumen = (1/3)πr²H

Wenn wir diese Werte in die Gleichung einsetzen, erhalten wir:

Volumen der Kugel = πr²h – (1/3)πr²h = (2/3)πr²H

Wir gehen davon aus, dass die Höhe des Zylinders dem Durchmesser der Kugel entspricht, der 2r beträgt. Daher:

Das Kugelvolumen beträgt (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Überprüfen Sie auch

• Formel für das Kugelkappenvolumen
• Kugelsektorformel
• Kugelsegmentformel

Wie berechnet man das Kugelvolumen?

Das Kugelvolumen ist der von einer Kugel eingenommene Raum. Sein Volumen kann mit der Formel berechnet werden V = 4/3πr ³ .

Zur Berechnung des Volumens einer Kugel sind folgende Schritte erforderlich:

Schritt 1: Markieren Sie den Wert des Kugelradius.

2. September: Finden Sie den Würfel des Radius.

Schritt 3: Multiplizieren Sie die dritte Potenz des Radius mit (4/3)π

Schritt 4: Fügen Sie die (Einheit) hinzu³zur endgültigen Antwort.

Beispiel zur Berechnung des Kugelvolumens

Beispiel: Ermitteln Sie das Volumen einer Kugel mit einem Radius von 7 cm.

Gegeben sei r = 7 cm

V = (4/3)πr³

Volumen der Kugel, V = ((4/3) × π × 7³) cm³

Höhe = 1436,8 cm³

Somit beträgt das Kugelvolumen 1436,8 cm³

Mehr lesen

• Volumen des Kegels
• Volumen des Würfels
• Volumen des Zylinders

Volumen der Kugelbeispiele

Beispiel 1. Ermitteln Sie das Volumen der Kugel mit einem Radius von 9 cm.

Lösung:

Es gilt r = 9

Kugelvolumen = 4/3 πr³

⇒ Volumen der Kugel = (4/3) (3,14) (9) (9) (9)

⇒ Volumen der Kugel = (4) (3,14) (3) (9) (9)

⇒ Kugelvolumen = 3052 cm³

Beispiel 2. Ermitteln Sie das Volumen der Kugel mit einem Radius von 12 cm.

Lösung:

Es gilt r = 12

Kugelvolumen = 4/3 πr³

⇒ Volumen der Kugel = (4/3) (3,14) (12) (12) (12)

⇒ Volumen der Kugel = (4) (3,14) (4) (12) (12)

⇒ Kugelvolumen = 7234,56 cm³

Beispiel 3. Ermitteln Sie das Volumen der Kugel mit einem Radius von 6 cm.

Lösung:

Es gilt r = 6

Kugelvolumen = 4/3 πr³

⇒ Volumen der Kugel = (4/3) (3,14) (6) (6) (6)

⇒ Volumen der Kugel = (4) (3.14) (2) (6) (6)

⇒ Kugelvolumen = 904,32 cm³

Beispiel 4. Ermitteln Sie das Volumen der Kugel mit einem Radius von 4 cm.

Lösung:

Es gilt r = 4

Kugelvolumen = 4/3 πr3

⇒ Volumen der Kugel = (4/3) (3,14) (4) (4) (4)

⇒ Volumen der Kugel = (1,33) (3,14) (4) (4) (4)

⇒ Kugelvolumen = 267,27 cm³

Beispiel 5. Ermitteln Sie das Volumen einer Kugel mit einem Durchmesser von 10 cm.

Lösung:

Wir haben 2r = 10

Stadt in den Vereinigten Staaten

⇒ r = 5

Kugelvolumen = 4/3 πr³

⇒ Volumen der Kugel = (4/3) (3,14) (5) (5) (5)

⇒ Volumen der Kugel = (1,33) (3,14) (5) (5) (5)

⇒ Kugelvolumen = 522,025 cm³

Beispiel 6. Ermitteln Sie das Volumen einer Kugel mit einem Durchmesser von 16 cm.

Lösung:

Wir haben 2r = 16

⇒ r = 8

Kugelvolumen = 4/3 πr³

⇒ Volumen der Kugel = (4/3) (3,14) (8) (8) (8)

⇒ Volumen der Kugel = (1,33) (3,14) (8) (8) (8)

⇒ Kugelvolumen = 2138,21 cm³

Beispiel 7. Ermitteln Sie das Volumen einer Kugel mit einem Durchmesser von 14 cm.

Lösung:

Wir haben 2r = 14

⇒ r = 7

Kugelvolumen = 4/3 πr³

⇒ Volumen der Kugel = (4/3) (3,14) (7) (7) (7)

⇒ Volumen der Kugel = (1,33) (3,14) (7) (7) (7)

⇒ Kugelvolumen = 1432,43 cm³

Umfang der Sphere-Practice-Fragen

F1: Finden Sie das Volumen der Kugel mit einem Durchmesser von 34 cm.

F2: Finden Sie das Volumen der Hohlkugel, deren Innenradius 4 cm und deren Außenradius 8 cm beträgt.

F3: Bestimmen Sie das Volumen der Kugel mit einem Radius von 14 cm.

F4: Wie groß ist das Volumen einer Kugel, deren Radius gleich der Seite eines Quadrats mit der Fläche 144 m ist?².

Umfang der Sphere-FAQs

Was ist das Kugelvolumen?

Das Kugelvolumen ist der von der Kugeloberfläche eingenommene Raum.

Was ist die Oberfläche einer Kugelformel?

Die Gesamtoberfläche der Kugel mit dem Radius r beträgt: Fläche = 4πr ²

Wie lautet die Formel für das Volumen einer Kugel?

Das Volumen einer Kugel mit dem Radius r ist: Volumen = 4/3πr ³

Wie finden wir das Volumen der Hemisphäre?

Das Volumen einer Halbkugel mit dem Radius r ist: Volumen = 2/3πr ³

Wie ist das Verhältnis des Volumens von Kugel und Halbkugel?

Wenn eine Kugel und eine Halbkugel den gleichen Radius haben, dann ist das Verhältnis ihrer Volumina:

IN ₁ : IN ₂ = (4/3πr ³ ): (2/3πr ³ ) = 2 : 1

Was ist die Volumeneinheit einer Kugel?

Das Volumen der Kugel wird in m gemessen³, cm³, Liter usw. M ³ ist die Standardmaßeinheit.

Wie groß ist das Volumen einer Kugel, wenn ihr Radius halbiert wird?

Kugelvolumen = (4/3)πr³= (4/3)π(r/2)³= (4/3)π(r³/8) = Lautstärke/8. Das Volumen der Kugel beträgt also ein Achtel.