Ein Binärbaum ist ausgeglichen, wenn die Höhe des Baums O(Log n) beträgt, wobei n die Anzahl der Knoten ist. Beispielsweise behält der AVL-Baum die Höhe O(Log n) bei, indem er sicherstellt, dass der Unterschied zwischen den Höhen des linken und rechten Teilbaums höchstens 1 beträgt. Rot-Schwarze Bäume behalten die Höhe O(Log n) bei, indem sie sicherstellen, dass die Zahl Die Anzahl der schwarzen Knoten auf jedem Wurzel-zu-Blatt-Pfad ist gleich und es gibt keine benachbarten roten Knoten. Ausgewogene binäre Suchbäume sind leistungsmäßig gut, da sie O(log n) Zeit zum Suchen, Einfügen und Löschen bereitstellen.

Ein ausgeglichener Binärbaum ist ein Binärbaum, der die drei Bedingungen erfüllt:

• Die Höhe des linken und rechten Baums unterscheidet sich für keinen Knoten um mehr als 1.
• Der linke Teilbaum dieses Knotens ist ebenfalls ausgeglichen.
• Der rechte Teilbaum dieses Knotens ist ebenfalls ausgeglichen.

Ein einzelner Knoten ist immer ausgeglichen. Er wird auch als höhenbalancierter Binärbaum bezeichnet.

Beispiel :

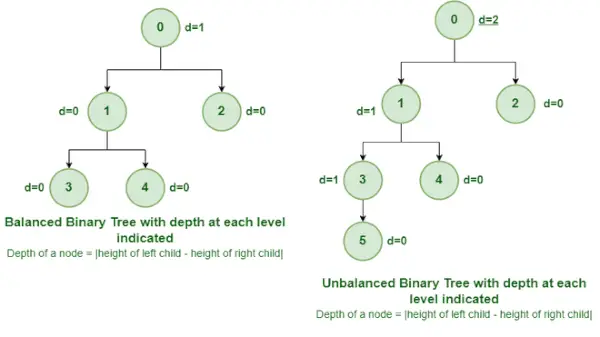
Ausgeglichener und unausgeglichener Binärbaum

Es handelt sich um eine Art Binärbaum, bei dem der Unterschied zwischen der Höhe des linken und rechten Teilbaums für jeden Knoten entweder 0 oder 1 beträgt. In der Abbildung oben ist der Wurzelknoten mit dem Wert 0 unausgeglichen und hat eine Tiefe von 2 Einheiten .

Anwendung des ausgeglichenen Binärbaums:

• AVL-Bäume
• Roter schwarzer Baum
• Ausgewogener binärer Suchbaum

Vorteile des ausgeglichenen Binärbaums:

• Zerstörungsfreie Updates werden von einem Balanced Binary Tree mit der gleichen asymptotischen Wirksamkeit unterstützt.
• Bereichsabfragen und Iterationen in der richtigen Reihenfolge werden durch den ausgeglichenen Binärbaum ermöglicht.