Eimersortierung ist eine Sortiertechnik, bei der Elemente in verschiedene Gruppen oder Buckets unterteilt werden. Diese Eimer entstehen durch gleichmäßige Verteilung der Elemente. Sobald die Elemente in Buckets unterteilt sind, können sie mit jedem anderen Sortieralgorithmus sortiert werden. Abschließend werden die sortierten Elemente geordnet zusammengetragen.
Wer hat die Schule gemacht?
Bucket-Sortieralgorithmus:
Erstellen N Leeren Sie Buckets (Oder-Listen) und führen Sie für jedes Array-Element arr[i] Folgendes aus:
- arr[i] in Bucket[n*array[i]] einfügen
- Sortieren Sie einzelne Buckets mithilfe der Einfügungssortierung.
- Verketten Sie alle sortierten Buckets.
Wie funktioniert Bucket Sort?
Anwenden der Bucket-Sortierung auf das Eingabearray [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , folgen wir diesen Schritten:
Schritt 1: Erstellen Sie ein Array der Größe 10, wobei jeder Slot einen Bucket darstellt.

Buckets zum Sortieren erstellen
Schritt 2: Fügen Sie Elemente basierend auf ihrem Bereich aus dem Eingabearray in die Buckets ein.
Elemente in die Buckets einfügen:
- Nehmen Sie jedes Element aus dem Eingabearray.
- Multiplizieren Sie das Element mit der Größe des Bucket-Arrays (in diesem Fall 10). Für Element 0,23 erhalten wir beispielsweise 0,23 * 10 = 2,3.
- Wandeln Sie das Ergebnis in eine Ganzzahl um, die uns den Bucket-Index ergibt. In diesem Fall wird 2,3 in die ganze Zahl 2 umgewandelt.
- Fügen Sie das Element in den Bucket ein, der dem berechneten Index entspricht.
- Wiederholen Sie diese Schritte für alle Elemente im Eingabearray.
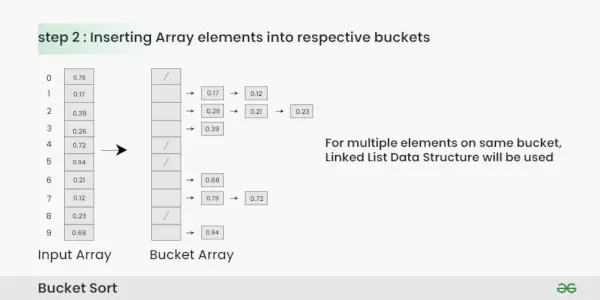
Einfügen von Array-Elementen in entsprechende Buckets
Schritt 3: Sortieren Sie die Elemente in jedem Bucket. In diesem Beispiel verwenden wir Quicksort (oder einen beliebigen stabilen Sortieralgorithmus), um die Elemente in jedem Bucket zu sortieren.
Sortieren der Elemente in jedem Bucket:
- Wenden Sie einen stabilen Sortieralgorithmus an (z. B. Bubble Sort, Merge Sort), um die Elemente in jedem Bucket zu sortieren.
- Die Elemente in jedem Bucket sind jetzt sortiert.
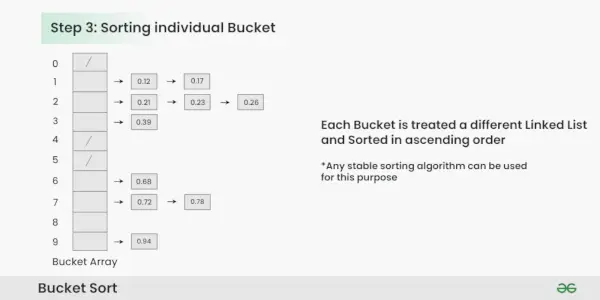
Sortieren einzelner Eimer
Schritt 4: Sammeln Sie die Elemente aus jedem Bucket und fügen Sie sie wieder in das ursprüngliche Array ein.
Array in Java
Sammeln von Elementen aus jedem Eimer:
Filme123 bis
- Durchlaufen Sie jeden Bucket der Reihe nach.
- Fügen Sie jedes einzelne Element aus dem Bucket in das ursprüngliche Array ein.
- Sobald ein Element kopiert wurde, wird es aus dem Bucket entfernt.
- Wiederholen Sie diesen Vorgang für alle Buckets, bis alle Elemente gesammelt sind.
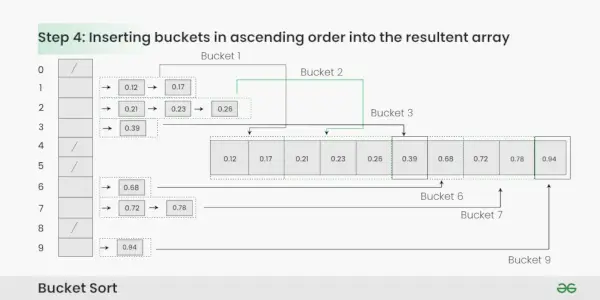
Einfügen von Buckets in aufsteigender Reihenfolge in das resultierende Array
Schritt 5: Das ursprüngliche Array enthält nun die sortierten Elemente.
Das endgültige sortierte Array mit Bucket-Sortierung für die gegebene Eingabe ist [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].

Gibt das sortierte Array zurück
Implementierung des Bucket-Sort-Algorithmus:
Nachfolgend finden Sie die Implementierung für die Bucket-Sortierung:
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& Bucket) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && Bucket[j]> key) { Bucket[j + 1] = Bucket[j]; J--; } Bucket[j + 1] = Schlüssel; } } // Funktion zum Sortieren von arr[] der Größe n mithilfe von Bucket Sort void BucketSort(float arr[], int n) { // 1) Erstelle n leere Buckets-Vektorb[n]; // 2) Array-Elemente in verschiedene Buckets legen für (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(ListBucket) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && Bucket.get(j)> Schlüssel) { Bucket.set(j + 1, Bucket.get(j)); J--; } Bucket.set(j + 1, Schlüssel); } } // Funktion zum Sortieren von arr[] der Größe n mithilfe der Bucket-Sortierung public static void BucketSort(float[] arr) { int n = arr.length; // 1) Erstellen Sie eine Liste mit n leeren Buckets[] Buckets = new ArrayList[n]; für (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 und Bucket[j]> Schlüssel: Bucket[j + 1] = Bucket[j] j -= 1 Bucket[j + 1] = Schlüssel def Bucket_sort(arr): n = len(arr) Buckets = [[] for _ in range(n)] # Array-Elemente in verschiedene Buckets für num in arr einfügen: bi = int(n * num) Buckets[bi].append(num) # Einzelne Buckets mit Einfügungssortierung für Bucket in Buckets sortieren: insert_sort (Bucket) # Verkettet alle Buckets in arr[] index = 0 für Bucket in Buckets: für Num in Bucket: arr[index] = Num Index += 1 arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434] Bucket_sort (arr) print('Sortiertes Array ist:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(ListBucket) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && Bucket[j]> key) { Bucket[j + 1] = Bucket[j]; J--; } Bucket[j + 1] = Schlüssel; } } // Funktion zum Sortieren von arr[] der Größe n mithilfe der Bucket-Sortierung static void BucketSort(float[] arr) { int n = arr.Length; // 1) Erstellen Sie eine Liste mit n leeren Buckets[] Buckets = neue Liste[N]; für (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Array-Elemente in verschiedene Buckets legen für (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && Bucket[j]> key) { Bucket[j + 1] = Bucket[j]; J--; } Bucket[j + 1] = Schlüssel; } } function BucketSort(arr) { let n = arr.length; let Buckets = Array.from({length: n}, () => []); // Array-Elemente in verschiedene Buckets legen for (let i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Ausgabe
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Komplexitätsanalyse des Bucket-Sort-Algorithmus:
Zeitkomplexität: An2),
- Wenn wir davon ausgehen, dass das Einfügen in einen Bucket O(1) Zeit benötigt, dann benötigen die Schritte 1 und 2 des obigen Algorithmus eindeutig O(n) Zeit.
- Das O(1) ist leicht möglich, wenn wir eine verknüpfte Liste zur Darstellung eines Buckets verwenden.
- Schritt 4 nimmt ebenfalls O(n) Zeit in Anspruch, da sich in allen Buckets n Elemente befinden.
- Der Hauptschritt der Analyse ist Schritt 3. Dieser Schritt benötigt im Durchschnitt auch O(n) Zeit, wenn alle Zahlen gleichmäßig verteilt sind.
Hilfsraum: O(n+k)
