
Gegeben a verbundener ungerichteter Graph dargestellt durch eine Adjazenzliste adjList[][] mit N Knoten und M Kanten, wobei jeder Knoten a hat eindeutiges Etikett aus 0 bis n-1 und jedes adj[i] stellt die Liste der Scheitelpunkte dar, die mit Scheitelpunkt i verbunden sind.
Erstellen Sie eine Klon des Diagramms, wobei jeder Knoten im Diagramm eine ganze Zahl enthält val und ein Array ( Nachbarn ) von Knoten enthält Knoten, die an den aktuellen Knoten angrenzen.
Klassenknoten {
Wert: Ganzzahl
Nachbarn: Liste[Knoten]
}1 von 1000
Ihre Aufgabe besteht darin, das angegebene Diagramm zu klonen und einen Verweis auf das geklonte Diagramm zurückzugeben.
Notiz: Wenn Sie eine korrekte Kopie des angegebenen Diagramms zurückgeben, ist die Ausgabe wahr. andernfalls wird bei einer fehlerhaften Kopie „False“ ausgegeben.
scanner.next Java
Beispiele
Eingang: n = 4 adjList[][] = [[1 2] [0 2] [0 1 3] [2]]
Ausgabe: WAHR
Erläuterung:
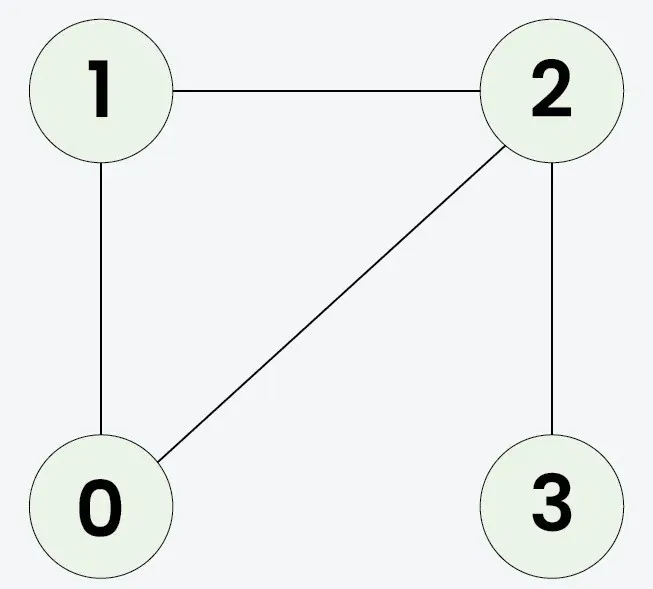
Da das geklonte Diagramm mit dem Original identisch ist, ist die Ausgabe wahr.Eingang: n = 3 adjList[][] = [[1 2] [0] [0]]
Ausgabe: WAHR
Erläuterung:
Da das geklonte Diagramm mit dem Original identisch ist, ist die Ausgabe wahr.
Inhaltsverzeichnis
- Warum müssen wir die besuchten/geklonten Knoten verfolgen?
- Wie behält man den Überblick über die besuchten/geklonten Knoten?
- Wie verbinde ich Klonknoten?
- Wie kann überprüft werden, ob das geklonte Diagramm korrekt ist?
- [Ansatz 1] Verwendung der BFS-Durchquerung – O(V+E)-Zeit und O(V)-Raum
- [Ansatz 2] Verwendung der DFS-Durchquerung – O(V+E)-Zeit und O(V)-Raum
Warum müssen wir die besuchten/geklonten Knoten verfolgen?
Wir müssen besuchte oder geklonte Knoten verfolgen, um eine unendliche Rekursion und redundante Arbeit beim Klonen eines Diagramms zu vermeiden. Da Diagramme Zyklen enthalten können (in denen ein Knoten auf einen zuvor besuchten Knoten verweisen kann), würde die Klonfunktion ohne Verfolgung der Knoten, die wir bereits geklont haben, endlos dieselben Knoten erneut aufrufen, was zu einem Stapelüberlauf oder einer falschen Duplizierung führen würde.
Wie behält man den Überblick über die besuchten/geklonten Knoten?
Um alle bereits erstellten Knoten zu verwalten, ist eine HashMap/Map erforderlich. Schlüsselgeschäfte : Referenz/Adresse des ursprünglichen Knotens Wertspeicher : Referenz/Adresse des geklonten Knotens. Es wurde eine Kopie aller Diagrammknoten erstellt.
Wie verbinde ich Klonknoten?
Beim Besuch der benachbarten Eckpunkte von a Knoten In Holen Sie sich das entsprechende Klon Knoten für dich nennen wir das so IN Besuchen Sie nun alle Nachbarknoten für In und für jeden Nachbarn den entsprechenden Klonknoten finden (falls nicht gefunden, erstellen Sie einen) und ihn dann in den benachbarten Vektor von verschieben IN Knoten.
Gimp löscht den Hintergrund
Wie kann überprüft werden, ob das geklonte Diagramm korrekt ist?
Führen Sie vor dem Klonen einen BFS-Durchlauf für das ursprüngliche Diagramm durch und dann erneut für das geklonte Diagramm, nachdem das Klonen abgeschlossen ist. Geben Sie bei jedem Durchlauf den Wert jedes Knotens zusammen mit seiner Adresse (oder Referenz) aus. Um die Korrektheit des Klonens zu überprüfen, vergleichen Sie die Reihenfolge der besuchten Knoten in beiden Durchläufen. Wenn die Knotenwerte in derselben Reihenfolge erscheinen, sich ihre Adressen (oder Referenzen) jedoch unterscheiden, bestätigt dies, dass das Diagramm erfolgreich und korrekt geklont wurde.
Erfahren Sie, wie es geht Klonen Sie einen ungerichteten Graphen, einschließlich Graphen mit mehreren verbundenen Komponenten Verwenden von BFS oder DFS, um eine vollständige tiefe Kopie aller Knoten und Kanten sicherzustellen.
Java ist eine Instanz von
[Ansatz 1] Verwendung der BFS-Durchquerung – O(V+E)-Zeit und O(V)-Raum
C++Beim BFS-Ansatz wird der Graph mithilfe einer Warteschlange iterativ geklont. Wir beginnen damit, den ursprünglichen Knoten zu klonen und ihn in die Warteschlange zu stellen. Während wir jeden Knoten aus der Warteschlange verarbeiten, besuchen wir seine Nachbarn. Wenn ein Nachbar noch nicht geklont wurde, erstellen wir einen Klon, speichern ihn in einer Karte und stellen ihn zur späteren Verarbeitung in die Warteschlange. Anschließend fügen wir den Klon des Nachbarn zur Liste der Nachbarn des Klons des aktuellen Knotens hinzu. Dieser Prozess wird Ebene für Ebene fortgesetzt und stellt sicher, dass alle Knoten in der Reihenfolge der Breite zuerst besucht werden. BFS ist besonders nützlich, um tiefe Rekursionen zu vermeiden und große oder breite Diagramme effizient zu verarbeiten.
#include
import java.util.*; // Definition for a Node class Node { public int val; public ArrayList<Node> neighbors; public Node() { neighbors = new ArrayList<>(); } public Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Clone the graph public static Node cloneGraph(Node node) { if (node == null) return null; Map<Node Node> mp = new HashMap<>(); Queue<Node> q = new LinkedList<>(); // Clone the starting node Node clone = new Node(node.val); mp.put(node clone); q.offer(node); while (!q.isEmpty()) { Node current = q.poll(); for (Node neighbor : current.neighbors) { // Clone neighbor if it hasn't been cloned yet if (!mp.containsKey(neighbor)) { mp.put(neighbor new Node(neighbor.val)); q.offer(neighbor); } // Add the clone of the neighbor to the current node's clone mp.get(current).neighbors.add(mp.get(neighbor)); } } return mp.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(new ArrayList<> (Arrays.asList(node2 node3))); node2.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node3))); node3.neighbors.addAll(new ArrayList<> (Arrays.asList(node1 node2 node4))); node4.neighbors.addAll(new ArrayList<> (Arrays.asList(node3))); return node1; } // Compare two graphs for structure and value public static boolean compareGraphs(Node n1 Node n2 HashMap<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || n1 == n2) return false; visited.put(n1 n2); if (n1.neighbors.size() != n2.neighbors.size()) return false; for (int i = 0; i < n1.neighbors.size(); i++) { Node neighbor1 = n1.neighbors.get(i); Node neighbor2 = n2.neighbors.get(i); if (visited.containsKey(neighbor1)) { if (visited.get(neighbor1) != neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void main(String[] args) { Node original = buildGraph(); Node cloned = cloneGraph(original); boolean isEqual = compareGraphs(original cloned new HashMap<>()); System.out.println(isEqual ? 'true' : 'false'); } }
from collections import deque # Definition for a Node class Node: def __init__(self val=0): self.val = val self.neighbors = [] # Clone the graph def cloneGraph(node): if not node: return None # Map to hold original nodes as keys and their clones as values mp = {} # Initialize BFS queue q = deque([node]) # Clone the starting node mp[node] = Node(node.val) while q: current = q.popleft() for neighbor in current.neighbors: # If neighbor not cloned yet if neighbor not in mp: mp[neighbor] = Node(neighbor.val) q.append(neighbor) # Link clone of neighbor to the clone of the current node mp[current].neighbors.append(mp[neighbor]) return mp[node] # Build graph def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs structurally and by values def compareGraphs(n1 n2 visited): if not n1 or not n2: return n1 == n2 if n1.val != n2.val or n1 is n2: return False visited[n1] = n2 if len(n1.neighbors) != len(n2.neighbors): return False for i in range(len(n1.neighbors)): neighbor1 = n1.neighbors[i] neighbor2 = n2.neighbors[i] if neighbor1 in visited: if visited[neighbor1] != neighbor2: return False else: if not compareGraphs(neighbor1 neighbor2 visited): return False return True # Driver if __name__ == '__main__': original = buildGraph() cloned = cloneGraph(original) result = compareGraphs(original cloned {}) print('true' if result else 'false')
using System; using System.Collections.Generic; // Definition for a Node public class Node { public int val; public List<Node> neighbors; public Node() { neighbors = new List<Node>(); } public Node(int val) { this.val = val; neighbors = new List<Node>(); } } class GfG { // Clone the graph public static Node CloneGraph(Node node) { if (node == null) return null; var mp = new Dictionary<Node Node>(); var q = new Queue<Node>(); // Clone the starting node var clone = new Node(node.val); mp[node] = clone; q.Enqueue(node); while (q.Count > 0) { var current = q.Dequeue(); foreach (var neighbor in current.neighbors) { // If neighbor not cloned clone it and enqueue if (!mp.ContainsKey(neighbor)) { mp[neighbor] = new Node(neighbor.val); q.Enqueue(neighbor); } // Add clone of neighbor to clone of current mp[current].neighbors.Add(mp[neighbor]); } } return mp[node]; } // Build graph public static Node BuildGraph() { var node1 = new Node(0); var node2 = new Node(1); var node3 = new Node(2); var node4 = new Node(3); node1.neighbors.AddRange(new[] { node2 node3 }); node2.neighbors.AddRange(new[] { node1 node3 }); node3.neighbors.AddRange(new[] { node1 node2 node4 }); node4.neighbors.AddRange(new[] { node3 }); return node1; } // Compare two graphs for structure and value public static bool CompareGraphs(Node n1 Node n2 Dictionary<Node Node> visited) { if (n1 == null || n2 == null) return n1 == n2; if (n1.val != n2.val || ReferenceEquals(n1 n2)) return false; visited[n1] = n2; if (n1.neighbors.Count != n2.neighbors.Count) return false; for (int i = 0; i < n1.neighbors.Count; i++) { var neighbor1 = n1.neighbors[i]; var neighbor2 = n2.neighbors[i]; if (visited.ContainsKey(neighbor1)) { if (!ReferenceEquals(visited[neighbor1] neighbor2)) return false; } else { if (!CompareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } public static void Main() { var original = BuildGraph(); var cloned = CloneGraph(original); var visited = new Dictionary<Node Node>(); Console.WriteLine(CompareGraphs(original cloned visited) ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Clone the graph function cloneGraph(node) { if (!node) return null; const mp = new Map(); const q = [node]; // Clone the initial node mp.set(node new Node(node.val)); while (q.length > 0) { const current = q.shift(); for (const neighbor of current.neighbors) { if (!mp.has(neighbor)) { mp.set(neighbor new Node(neighbor.val)); q.push(neighbor); } // Link clone of neighbor to clone of current mp.get(current).neighbors.push(mp.get(neighbor)); } } return mp.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors = [node2 node3]; node2.neighbors = [node1 node3]; node3.neighbors = [node1 node2 node4]; node4.neighbors = [node3]; return node1; } // Compare two graphs structurally and by value function compareGraphs(n1 n2 visited = new Map()) { if (!n1 || !n2) return n1 === n2; if (n1.val !== n2.val || n1 === n2) return false; visited.set(n1 n2); if (n1.neighbors.length !== n2.neighbors.length) return false; for (let i = 0; i < n1.neighbors.length; i++) { const neighbor1 = n1.neighbors[i]; const neighbor2 = n2.neighbors[i]; if (visited.has(neighbor1)) { if (visited.get(neighbor1) !== neighbor2) return false; } else { if (!compareGraphs(neighbor1 neighbor2 visited)) return false; } } return true; } // Driver const original = buildGraph(); const cloned = cloneGraph(original); const result = compareGraphs(original cloned); console.log(result ? 'true' : 'false');
Ausgabe
true
[Ansatz 2] Verwendung der DFS-Durchquerung – O(V+E)-Zeit und O(V)-Raum
C++Beim DFS-Ansatz wird der Graph mittels Rekursion geklont. Wir beginnen am angegebenen Knoten und erkunden jeden Zweig so weit wie möglich, bevor wir zurückgehen. Eine Karte (oder ein Wörterbuch) wird verwendet, um den Überblick über bereits geklonte Knoten zu behalten, um zu vermeiden, dass derselbe Knoten mehrmals verarbeitet wird, und um Zyklen zu bewältigen. Wenn wir zum ersten Mal auf einen Knoten stoßen, erstellen wir einen Klon davon und speichern ihn in der Karte. Dann klonen wir jeden Nachbarn dieses Knotens rekursiv und fügen den geklonten Nachbarn zum Klon des aktuellen Knotens hinzu. Dadurch wird sichergestellt, dass alle Knoten vor der Rückkehr gründlich besucht werden und die Diagrammstruktur originalgetreu kopiert wird.
#include
import java.util.*; // Definition for a Node class Node { int val; ArrayList<Node> neighbors; Node() { neighbors = new ArrayList<>(); } Node(int val) { this.val = val; neighbors = new ArrayList<>(); } } public class GfG { // Map to hold original node to its copy static HashMap<Node Node> copies = new HashMap<>(); // Function to clone the graph using DFS public static Node cloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.containsKey(node)) { Node clone = new Node(node.val); copies.put(node clone); // Recursively clone neighbors for (Node neighbor : node.neighbors) { clone.neighbors.add(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph public static Node buildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.addAll(Arrays.asList(node2 node3)); node2.neighbors.addAll(Arrays.asList(node1 node3)); node3.neighbors.addAll(Arrays.asList(node1node2 node4)); node4.neighbors.addAll(Arrays.asList(node3)); return node1; } // Compare two graphs for structural and value equality public static boolean compareGraphs(Node node1 Node node2 HashMap<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited.put(node1 node2); if (node1.neighbors.size() != node2.neighbors.size()) return false; for (int i = 0; i < node1.neighbors.size(); i++) { Node n1 = node1.neighbors.get(i); Node n2 = node2.neighbors.get(i); if (visited.containsKey(n1)) { if (visited.get(n1) != n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void main(String[] args) { Node original = buildGraph(); // Clone the graph Node cloned = cloneGraph(original); // Compare original and cloned graph boolean result = compareGraphs(original cloned new HashMap<>()); System.out.println(result ? 'true' : 'false'); } }
# Definition for a Node class Node: def __init__(self val=0 neighbors=None): self.val = val self.neighbors = neighbors if neighbors is not None else [] # Map to hold original node to its copy copies = {} # Function to clone the graph def cloneGraph(node): # If the node is None return None if not node: return None # If node is not yet cloned clone it if node not in copies: # Create a clone of the node clone = Node(node.val) copies[node] = clone # Recursively clone neighbors for neighbor in node.neighbors: clone.neighbors.append(cloneGraph(neighbor)) # Return the clone return copies[node] def buildGraph(): node1 = Node(0) node2 = Node(1) node3 = Node(2) node4 = Node(3) node1.neighbors = [node2 node3] node2.neighbors = [node1 node3] node3.neighbors = [node1 node2 node4] node4.neighbors = [node3] return node1 # Compare two graphs for structural and value equality def compareGraphs(node1 node2 visited): if not node1 or not node2: return node1 == node2 if node1.val != node2.val or node1 is node2: return False visited[node1] = node2 if len(node1.neighbors) != len(node2.neighbors): return False for i in range(len(node1.neighbors)): n1 = node1.neighbors[i] n2 = node2.neighbors[i] if n1 in visited: if visited[n1] != n2: return False else: if not compareGraphs(n1 n2 visited): return False return True # Driver Code if __name__ == '__main__': original = buildGraph() # Clone the graph using DFS cloned = cloneGraph(original) # Compare original and cloned graph visited = {} print('true' if compareGraphs(original cloned visited) else 'false')
using System; using System.Collections.Generic; public class Node { public int val; public List<Node> neighbors; public Node() { val = 0; neighbors = new List<Node>(); } public Node(int _val) { val = _val; neighbors = new List<Node>(); } } class GfG { // Dictionary to hold original node to its copy static Dictionary<Node Node> copies = new Dictionary<Node Node>(); // Function to clone the graph using DFS public static Node CloneGraph(Node node) { // If the node is NULL return NULL if (node == null) return null; // If node is not yet cloned clone it if (!copies.ContainsKey(node)) { Node clone = new Node(node.val); copies[node] = clone; // Recursively clone neighbors foreach (Node neighbor in node.neighbors) { clone.neighbors.Add(CloneGraph(neighbor)); } } // Return the clone return copies[node]; } // Build graph public static Node BuildGraph() { Node node1 = new Node(0); Node node2 = new Node(1); Node node3 = new Node(2); Node node4 = new Node(3); node1.neighbors.Add(node2); node1.neighbors.Add(node3); node2.neighbors.Add(node1); node2.neighbors.Add(node3); node3.neighbors.Add(node1); node3.neighbors.Add(node2); node3.neighbors.Add(node4); node4.neighbors.Add(node3); return node1; } // Compare two graphs for structural and value equality public static bool CompareGraphs(Node node1 Node node2 Dictionary<Node Node> visited) { if (node1 == null || node2 == null) return node1 == node2; if (node1.val != node2.val || node1 == node2) return false; visited[node1] = node2; if (node1.neighbors.Count != node2.neighbors.Count) return false; for (int i = 0; i < node1.neighbors.Count; i++) { Node n1 = node1.neighbors[i]; Node n2 = node2.neighbors[i]; if (visited.ContainsKey(n1)) { if (visited[n1] != n2) return false; } else { if (!CompareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code public static void Main() { Node original = BuildGraph(); // Clone the graph using DFS Node cloned = CloneGraph(original); // Compare original and cloned graph bool isEqual = CompareGraphs(original cloned new Dictionary<Node Node>()); Console.WriteLine(isEqual ? 'true' : 'false'); } }
// Definition for a Node class Node { constructor(val = 0) { this.val = val; this.neighbors = []; } } // Map to hold original node to its copy const copies = new Map(); // Function to clone the graph using DFS function cloneGraph(node) { // If the node is NULL return NULL if (node === null) return null; // If node is not yet cloned clone it if (!copies.has(node)) { const clone = new Node(node.val); copies.set(node clone); // Recursively clone neighbors for (let neighbor of node.neighbors) { clone.neighbors.push(cloneGraph(neighbor)); } } // Return the clone return copies.get(node); } // Build graph function buildGraph() { const node1 = new Node(0); const node2 = new Node(1); const node3 = new Node(2); const node4 = new Node(3); node1.neighbors.push(node2 node3); node2.neighbors.push(node1 node3); node3.neighbors.push(node1 node2 node4); node4.neighbors.push(node3); return node1; } // Compare two graphs for structural and value equality function compareGraphs(node1 node2 visited = new Map()) { if (!node1 || !node2) return node1 === node2; if (node1.val !== node2.val || node1 === node2) return false; visited.set(node1 node2); if (node1.neighbors.length !== node2.neighbors.length) return false; for (let i = 0; i < node1.neighbors.length; i++) { const n1 = node1.neighbors[i]; const n2 = node2.neighbors[i]; if (visited.has(n1)) { if (visited.get(n1) !== n2) return false; } else { if (!compareGraphs(n1 n2 visited)) return false; } } return true; } // Driver Code const original = buildGraph(); // Clone the graph using DFS const cloned = cloneGraph(original); // Compare original and cloned graph console.log(compareGraphs(original cloned) ? 'true' : 'false');
Ausgabe
true


