Faltung wird für viele Dinge wie die Berechnung von Ableitungen, das Erkennen von Kanten, das Anwenden von Unschärfen usw. verwendet und all dies wird mithilfe eines „Faltungskerns“ durchgeführt. Ein Faltungskern ist eine sehr kleine Matrix und in dieser Matrix hat jede Zelle eine Zahl und auch einen Ankerpunkt.
Der Ankerpunkt wird verwendet, um die Position des Kernels in Bezug auf das Bild zu kennen. Es beginnt in der oberen linken Ecke des Bildes und bewegt sich nacheinander auf jedem Pixel weiter. Der Kernel überlappt an jeder Position im Bild einige Pixel. Jedes überlappende Pixel wird multipliziert und dann addiert. Und die Summe wird als Wert der aktuellen Position gesetzt.
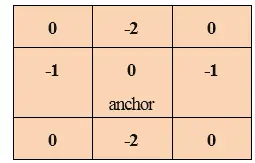
Faltung ist der Prozess, bei dem jedes Element des Bildes zu seinen lokalen Nachbarn hinzugefügt und dann vom Kernel gewichtet wird. Es hängt mit einer Form der mathematischen Faltung zusammen.
Bei der Faltung führt die Matrix keine herkömmliche Matrixmultiplikation durch, wird jedoch mit * gekennzeichnet.
Angenommen, es gibt zwei 3x3-Matrizen, eine ist der Kernel und eine andere ist ein Bildstück. Bei der Faltung werden Zeilen und Spalten des Kernels umgedreht, dann multipliziert und anschließend summiert. Elemente, die in der Mitte der Matrix, d. h. in [2,2] des Bildes, vorhanden sind, werden eine gewichtete Kombination der Bildmatrix sein und die Gewichte werden vom Kernel vorgegeben. In ähnlicher Weise werden alle anderen Elemente der Matrix gewichtet und anschließend werden die Gewichte berechnet.
Im Folgenden finden Sie Pseudocode zur Beschreibung des Faltungsprozesses:
For each image row in input image: For each pixel in image row: Set accumulator to zero For each kernel row in kernel: For each element in kernel row: If element position corresponding* to pixel position then Multiply element value corresponding*to pixelvalue Add result to accumulator Endif Set output image pixel to accumulator
Die Faltung kann mithilfe mehrerer for-Schleifen berechnet werden. Die Verwendung von for-Schleifen verursacht jedoch viele wiederholte Berechnungen und außerdem nimmt die Größe von Bild und Kernel zu. Mit der Technik der diskreten Fourier-Transformation kann die Berechnung der Faltung schnell durchgeführt werden. Bei dieser Technik wird die gesamte Faltungsoperation in eine einfache Multiplikation umgewandelt.
Bei der Faltung tritt das Problem auf, wenn sich der Kernel in der Nähe von Kanten oder Ecken befindet, da der Kernel zweidimensional ist.
Um diese Probleme zu überwinden, können folgende Dinge getan werden:
- Einsen können ignoriert werden
- In Randnähe können zusätzliche Pixel entstehen.
Zusätzliche Pixel können auf folgende Weise erstellt werden:
- Doppeltes Kantenpixel.
- Kanten spiegeln
- Pixel können vom anderen Ende kopiert werden.
