Divide and Conquer ist ein algorithmisches Muster. Bei algorithmischen Methoden besteht das Design darin, einen Streit über eine große Eingabe zu nehmen, die Eingabe in kleinere Teile zu zerlegen, das Problem für jedes der kleinen Teile zu entscheiden und dann die stückweisen Lösungen zu einer globalen Lösung zusammenzuführen. Dieser Mechanismus zur Lösung des Problems wird Divide & Conquer-Strategie genannt.

Der Divide and Conquer-Algorithmus besteht aus einem Streit mit den folgenden drei Schritten.

TeilenDas ursprüngliche Problem wird in eine Reihe von Teilproblemen zerlegt.Erobern:Lösen Sie jedes Teilproblem einzeln und rekursiv.Kombinieren:Fügen Sie die Lösungen der Teilprobleme zusammen, um die Lösung des gesamten Problems zu erhalten.

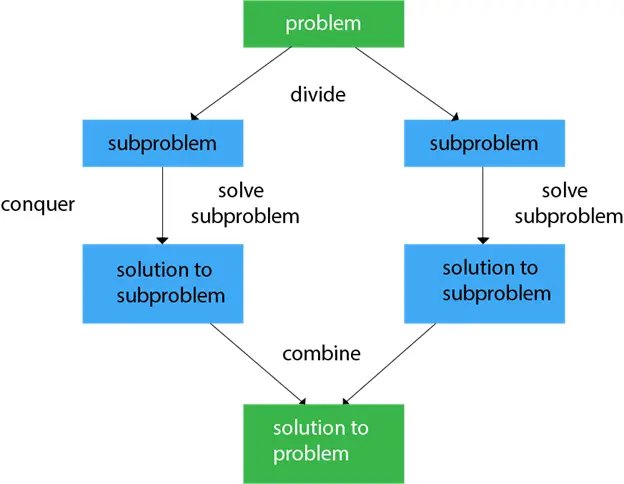
Im Allgemeinen können wir dem folgen Teile und herrsche Vorgehensweise in einem dreistufigen Prozess.

Beispiele: Die spezifischen Computeralgorithmen basieren auf dem Divide & Conquer-Ansatz:

1. Maximales und minimales Problem
2. Binäre Suche
3. Sortieren (Zusammenführungssortierung, Schnellsortierung)
4. Turm von Hanoi.

Grundlagen der Divide & Conquer-Strategie:

Es gibt zwei grundlegende Aspekte der Divide & Conquer-Strategie:

1. Beziehungsformel
2. Stoppbedingung

1. Beziehungsformel: Es ist die Formel, die wir aus der gegebenen Technik generieren. Nach der Generierung der Formel wenden wir die D&C-Strategie an, d. h. wir brechen das Problem rekursiv auf und lösen die kaputten Teilprobleme.

2. Stoppbedingung: Wenn wir das Problem mithilfe der Divide & Conquer-Strategie lösen, müssen wir wissen, wie lange wir Divide & Conquer anwenden müssen. Daher wird die Bedingung, bei der unsere Rekursionsschritte von D&C gestoppt werden müssen, als Stoppbedingung bezeichnet.

Anwendungen des Divide and Conquer-Ansatzes:

Die folgenden Algorithmen basieren auf dem Konzept der Divide and Conquer-Technik:

Binäre Suche:Der binäre Suchalgorithmus ist ein Suchalgorithmus, der auch als Halbintervallsuche oder logarithmische Suche bezeichnet wird. Dabei wird der Zielwert mit dem mittleren Element verglichen, das in einem sortierten Array vorhanden ist. Wenn nach dem Vergleich der Wert abweicht, wird schließlich die Hälfte, die das Ziel nicht enthalten kann, eliminiert, und anschließend wird die Suche in der anderen Hälfte fortgesetzt. Wir betrachten noch einmal das mittlere Element und vergleichen es mit dem Zielwert. Der Vorgang wiederholt sich so lange, bis der Zielwert erreicht ist. Wenn wir nach Beendigung der Suche feststellen, dass die andere Hälfte leer ist, können wir daraus schließen, dass das Ziel nicht im Array vorhanden ist.Schnelle Sorte:Es handelt sich um den effizientesten Sortieralgorithmus, der auch als Partition-Exchange-Sortierung bezeichnet wird. Es beginnt mit der Auswahl eines Pivotwerts aus einem Array, gefolgt von der Aufteilung der restlichen Array-Elemente in zwei Unterarrays. Die Partitionierung erfolgt durch den Vergleich jedes Elements mit dem Pivotwert. Es vergleicht, ob das Element einen größeren oder kleineren Wert als der Pivot enthält, und sortiert dann die Arrays rekursiv.Zusammenführen, sortieren:Es handelt sich um einen Sortieralgorithmus, der ein Array durch Vergleiche sortiert. Es beginnt mit der Aufteilung eines Arrays in Unterarrays und sortiert dann jedes einzelne rekursiv. Nachdem die Sortierung abgeschlossen ist, werden sie wieder zusammengeführt.Nächstes Punktepaar:Es handelt sich um ein Problem der Computergeometrie. Bei diesem Algorithmus liegt der Schwerpunkt darauf, bei gegebenen n Punkten das nächstgelegene Punktpaar in einem metrischen Raum zu ermitteln, sodass der Abstand zwischen dem Punktpaar minimal sein sollte.Strassen's Algorithm:Es handelt sich um einen Algorithmus zur Matrizenmultiplikation, der nach Volker Strassen benannt ist. Es hat sich gezeigt, dass er bei der Arbeit mit großen Matrizen viel schneller ist als der herkömmliche Algorithmus.Cooley-Tukey-Algorithmus der Fast-Fourier-Transformation (FFT):Der Algorithmus der schnellen Fourier-Transformation ist nach J. W. Cooley und John Turkey benannt. Es folgt dem Divide-and-Conquer-Ansatz und erzwingt eine Komplexität von O(nlogn).Karatsuba-Algorithmus für schnelle Multiplikation:Es handelt sich um einen der schnellsten Multiplikationsalgorithmen der Menschheit, der Ende 1960 von Anatoly Karatsuba erfunden und 1962 veröffentlicht wurde. Er multipliziert zwei n-stellige Zahlen auf diese Weise, indem er sie auf maximal eine Ziffer reduziert.

Vorteile von Divide and Conquer

• „Teile und herrsche“ tendiert dazu, eines der größten Probleme erfolgreich zu lösen, beispielsweise den Turm von Hanoi, ein mathematisches Rätsel. Es ist eine Herausforderung, komplizierte Probleme zu lösen, von denen man keine Grundidee hat, aber mit Hilfe des Divide-and-Conquer-Ansatzes hat es den Aufwand verringert, da es darum geht, das Hauptproblem in zwei Hälften zu teilen und diese dann rekursiv zu lösen. Dieser Algorithmus ist viel schneller als andere Algorithmen.
• Es nutzt den Cache-Speicher effizient, ohne viel Platz zu beanspruchen, da es einfache Teilprobleme im Cache-Speicher löst, anstatt auf den langsameren Hauptspeicher zuzugreifen.
• Sie ist leistungsfähiger als die entsprechende Brute-Force-Technik.
• Da diese Algorithmen die Parallelität verhindern, sind keine Änderungen erforderlich und die Verarbeitung erfolgt durch Systeme mit Parallelverarbeitung.

Nachteile von Divide and Conquer

• Da die meisten seiner Algorithmen auf Rekursion basieren, ist eine hohe Speicherverwaltung erforderlich.
• Ein expliziter Stapel kann den Speicherplatz überbeanspruchen.
• Es kann sogar zum Absturz des Systems kommen, wenn die Rekursion deutlich größer ist als der in der CPU vorhandene Stapel.