In diesem Artikel besprechen wir das Runden von Zahlen in Python mit geeigneten Methoden und Beispielen So runden Sie ab Python .

Beispiel:

  Input:   3.5   Output:   4   Explanation:   Nearest whole number.   Input:   3.74   Output:   3.7   Explanation:   Rounded to one decimal place.>

Zahlen in Python aufrunden

Eine Zahl zu runden bedeutet, die Zahl einfacher zu machen, indem ihr Wert erhalten bleibt, aber näher an der nächsten Zahl liegt. Es gibt verschiedene Methoden zum Runden von Zahlen in Python. Hier besprechen wir einige, die allgemein verwendet werden So runden Sie in Python auf Im Folgenden sind die folgenden Punkte aufgeführt, die in diesem Artikel mithilfe von Python behandelt werden:

• Verwendung der integrierten Funktion „round()“.
• Benutzen Kürzung Konzept
• Benutzen Math.ceil() Und Math.floor() Funktionen
• Benutzen math.ceil
• Benutzen Mathe.Boden
• Verwendung der numpy> Modul
• Verwendung der Rundung Bias-Konzept
• In Python die Hälfte von Null abrunden
  

Runde Zahlen in Python u singen Eingebaut runden() Funktion

In Python gibt es eine integrierte Funktion Round()-Funktion Das rundet eine Zahl auf die angegebene Anzahl von Stellen ab. Die Funktion „round()“ akzeptiert zwei numerische Argumente, n und n Ziffern, und gibt dann die Zahl n zurück, nachdem sie auf n Ziffern gerundet wurde. Wenn die Anzahl der Stellen zum Abrunden nicht angegeben ist, rundet die Funktion die angegebene Zahl n auf die nächste ganze Zahl auf.

Javascript-Benachrichtigungsfeld

Beispiel : In diesem Beispiel zeigt der folgende Code die Funktion „round()“ für Ganzzahlen und Gleitkommazahlen. Es veranschaulicht auch das Runden auf zwei Dezimalstellen und zeigt Fälle auf, in denen die nächste Ziffer 5, größer als 5 und kleiner als 5 ist.

Python3

>

>

Ausgabe:

11 23 4.46 4.48 4.47>

Runde Zahlen in Python u singen Kürzung Konzept

In dieser Funktion wird jede Ziffer nach einer bestimmten Position durch 0 ersetzt. Python kürzen() Funktion kann sowohl mit positiven als auch mit negativen Zahlen verwendet werden. Die Trunkierungsfunktion kann folgendermaßen implementiert werden:

• Multiplizieren Sie die Zahl mit 10^p (10 erhöht auf p)._ThPotenz), um den Dezimalpunkt um p Stellen nach rechts zu verschieben.
• Den ganzzahligen Teil dieser neuen Zahl mit int() nehmen.
• Durch Division durch 10^p wird die Dezimalstelle p nach links verschoben.

Python3

>

>

Ausgabe:

16.0 -3.8 3.81 340.0 -2000.0>

Runde Zahlen in Python u singen Math.ceil() Und Math.floor() Funktionen

Mathematik . Decke() : Diese Funktion gibt die nächste Ganzzahl zurück, die größer oder gleich einer bestimmten Zahl ist.
Math.floor() : Diese Funktion gibt die nächste ganze Zahl zurück, die kleiner oder gleich einer bestimmten Zahl ist.

Beispiel :In diesem Beispiel verwendet der folgende Code die „math“-Bibliothek, um Obergrenzenwerte für positive und negative Dezimalzahlen mit „math.ceil“ und Untergrenzenwerte mit „math.floor“ zu berechnen. Die Ausgaben sind 5, 0, 2 und -1 für die jeweiligen Fälle.

Python3

>

>

Ausgabe:

5 0 2 -1>

Runde Zahlen in Python u singe math.ceil

Um eine Zahl aufzurunden, müssen Sie den Dezimalpunkt nach rechts verschieben, aufrunden und ihn dann aus Präzisionsgründen mit „`“ wieder nach links verschieben math.ceil() ` und Multiplikations-/Divisionsoperationen.

Beispiel :In diesem Beispiel definiert der folgende Code eine „round_up“-Funktion mithilfe der „math“-Bibliothek, die eine Zahl auf eine angegebene Dezimalstelle rundet. Für die Präzision werden Multiplikation, Rundung mit „math.ceil()“ und Division verwendet. Positive und negative Werte werden auf Rundung geprüft.

Python3

>

>

Ausgabe:

3.0 2.3 2.55 30.0 2400.0>

Wir können dem Diagramm unten folgen, um das Auf- und Abrunden zu verstehen. Runden Sie nach rechts auf und nach links ab.

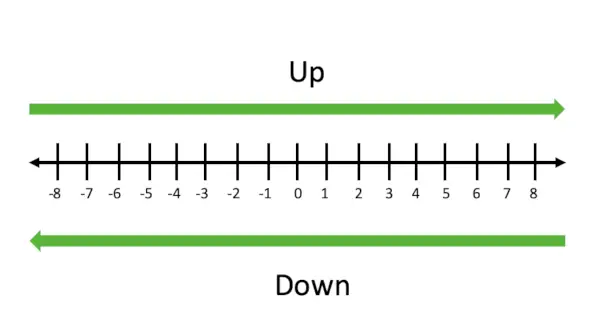
Beim Aufrunden wird eine Zahl immer nach rechts auf der Zahlengeraden gerundet, beim Abrunden wird eine Zahl immer nach links auf der Zahlengeraden gerundet.

Runde Zahlen in Python u singen Mathe.Boden

Beim Abrunden wird eine Zahl auf eine bestimmte Anzahl von Stellen abgerundet. Die Abrundungsfunktion kann folgendermaßen implementiert werden:

• Zunächst wird der Dezimalpunkt in n um die richtige Anzahl Stellen nach rechts verschoben, indem n mit 10 ** Dezimalstellen multipliziert wird.
• Der neue Wert wird mit auf die nächste Ganzzahl aufgerundet math.floor() .
• Abschließend wird der Dezimalpunkt durch Division durch 10 ** Dezimalstellen wieder nach links verschoben.

Python3

>

>

Ausgabe:

2.0 2.4 -1.0>

Runde Zahlen in Python u singen Numpy Modul

Das NumPy-Modul in Python bietet das numpy.round()>Funktion um Zahlen zu runden. Diese Funktion rundet jedes Element eines Arrays auf die nächste ganze Zahl oder auf die angegebene Anzahl von Dezimalstellen.

Beispiel : In diesem Beispiel verwendet der folgende Code das NumPy-Modul, um ein Array „arr“ zu erstellen und jedes Element auf die nächste Ganzzahl („rounded_integers“) und auf zwei Dezimalstellen („rounded_decimals“) zu runden. Die Ergebnisse werden dann zur Anzeige ausgedruckt.

Python3

>

>

Ausgabe :

Nearest integer: [1. 3. 4.] Decimal places: [1.23 2.57 3.79]>

Runde Zahlen in Python u singen Rundungsbias Konzept.

Das Konzept der Symmetrie führt den Begriff des Rundungsbias ein, der beschreibt, wie sich Rundungen auf numerische Daten in einem Datensatz auswirken.
Die Aufrundungsstrategie weist eine Tendenz zur Rundung in Richtung positiver Unendlichkeit auf, da der Wert immer in Richtung positiver Unendlichkeit aufgerundet wird. In ähnlicher Weise hat die Abrundungsstrategie eine Tendenz zur Abrundung in Richtung negativer Unendlichkeit. Die Trunkierungsstrategie hat eine Rundung in Richtung negativer Unendlichkeit bei positiven Werten und eine Rundung in Richtung positiver Unendlichkeit bei negativen Werten. Bei Rundungsfunktionen mit diesem Verhalten spricht man im Allgemeinen von einer Rundung in Richtung Null.

a) Zur Hälfte aufrunden Konzept in Python

Beim Halbaufrunden wird jede Zahl mit der angegebenen Genauigkeit auf die nächste Zahl gerundet und Gleichstände werden durch Aufrunden aufgehoben.
Die Halbaufrundungsstrategie wird umgesetzt, indem der Dezimalpunkt um die gewünschte Anzahl Stellen nach rechts verschoben wird. In diesem Fall müssen wir feststellen, ob die Ziffer nach dem verschobenen Dezimalpunkt kleiner oder größer gleich 5 ist.
Wir können 0,5 zum verschobenen Wert addieren und ihn dann mit der Funktion math.floor() abrunden.

Implementierung der Funktion „round_half_up()“:

Beispiel: In diesem Beispiel definiert der folgende Code „round_half_up“, eine benutzerdefinierte Rundungsfunktion, die die Round-Half-Up-Methode mit „math.floor()“ für Präzision verwendet. Die Demonstrationen umfassen positive und negative Zahlen mit verschiedenen Dezimalstellen.

Python3

>

>

Ausgabe:

1.3 -1.0 -1.23>

b) Auf die Hälfte abrunden Konzept in Python

Dabei wird auf die nächstliegende Zahl gerundet, ähnlich wie bei der Halbaufrundungsmethode. Der Unterschied besteht darin, dass Unentschieden durch Aufrunden auf die kleinere der beiden Zahlen aufgehoben werden. Die Strategie zum Halbieren wird implementiert, indem math.floor() in der Funktion „round_half_up()“ durch math.ceil() ersetzt und dann 0,5 subtrahiert statt addiert wird.

Implementierung der Funktion „round_half_down()“:

In diesem Beispiel definiert der folgende Code „round_half_down“ mithilfe der „math“-Bibliothek, um ein Round-Half-Down-Verhalten zu erreichen. Es nutzt Multiplikation, Subtraktion und „math.ceil()“ zum Runden gegen Null. Testfälle umfassen positive und negative Dezimalzahlen, wobei auf eine Dezimalstelle gerundet wird.

Python3

>

>

Ausgabe:

2.0 -3.0 2.2>

In Python die Hälfte von Null abrunden

Beim Runden um die Hälfte von Null beginnen wir wie üblich damit, den Dezimalpunkt um eine bestimmte Anzahl von Stellen nach rechts zu verschieben und dann die Ziffer (d) unmittelbar rechts von der Dezimalstelle in der neuen Zahl zu bemerken. Es sind vier Fälle zu berücksichtigen:

• Wenn n positiv und d>= 5 ist, runden Sie auf
• Wenn n positiv und d = 5 ist, runden Sie ab
• Wenn n negativ ist und d>= 5, runden Sie ab
• Wenn n negativ und d <5 ist, wird aufgerundet

Nachdem wir gemäß den oben genannten Regeln gerundet haben, können wir die Dezimalstelle wieder nach links verschieben.

• Von halb auf gerade runden: Es gibt eine Möglichkeit, den Rundungsfehler beim Runden von Werten in einem Datensatz zu verringern. Wir können Bindungen einfach mit der gewünschten Genauigkeit auf die nächste gerade Zahl runden. Die Halb-auf-Gerade-Rundungsstrategie ist die Strategie, die von Pythons integrierter Round() verwendet wird. Der Dezimalklasse Bietet Unterstützung für schnelle, korrekt gerundete dezimale Gleitkomma-Arithmetik. Dies bietet mehrere Vorteile gegenüber dem Float-Datentyp. Die Standardrundungsstrategie im Dezimalmodul ist ROUND_HALF_EVEN.

Beispiel: In diesem Beispiel verwendet der folgende Code die Funktion „Decimal“ aus der Bibliothek „decimal“, um Dezimalzahlen präzise darzustellen. Es steht im Gegensatz zum Erstellen eines „Decimal“-Objekts aus einer Zeichenfolge und direkt aus einer Gleitkommazahl. Die Funktion „quantize()“ wird dann zum Runden mit angegebenen Dezimalstellen verwendet und demonstriert so die Präzision in der Dezimalarithmetik.

Python3

>

>

Ausgabe:

0.1 0.1000000000000000055511151231257827021181583404541015625 1.6 1.68>