Die Welt der Algorithmen ist wunderschön, mit vielfältigen Strategien und Tools, die rund um die Uhr entwickelt werden, um den Anforderungen an Hochleistungsrechnen gerecht zu werden. Tatsächlich werden interessante Ergebnisse beobachtet, wenn Algorithmen von Naturgesetzen inspiriert werden. Evolutionäre Algorithmen gehören zu einer solchen Klasse von Algorithmen. Diese Algorithmen sind so konzipiert, dass sie bestimmte Verhaltensweisen sowie evolutionäre Merkmale des menschlichen Genoms nachahmen. Darüber hinaus ist ein solches algorithmisches Design nicht nur auf den Menschen beschränkt, sondern kann auch vom natürlichen Verhalten bestimmter Tiere inspiriert werden. Das grundlegende Ziel bei der Entwicklung solcher Methoden besteht darin, realistische, relevante und dennoch kostengünstige Lösungen für Probleme bereitzustellen, die bisher mit herkömmlichen Mitteln nicht lösbar sind.

Basierend auf solchen evolutionären Algorithmen haben sich daher verschiedene Optimierungstechniken entwickelt und damit den Bereich der Metaheuristiken eröffnet. Metaheuristisch wurde von zwei griechischen Wörtern abgeleitet, nämlich: Meta Bedeutung eine Ebene darüber Und heuriskein Bedeutung finden . Algorithmen wie die Particle Swarm Optimization (PSO) und Ant Colony Optimization (ACO) sind Beispiele für Schwarmintelligenz und Metaheuristik. Das Ziel der Schwarmintelligenz besteht darin, intelligente Multiagentensysteme zu entwerfen, indem sie sich vom kollektiven Verhalten sozialer Insekten wie Ameisen, Termiten, Bienen, Wespen und anderen Tiergesellschaften wie Vogelschwärmen oder Fischschwärmen inspirieren lässt.

Hintergrund:

Die Technik der Ameisenkolonie-Optimierung ist rein von der inspiriert Nahrungssuche Verhalten von Ameisenkolonien, erstmals in den 1990er Jahren von Marco Dorigo eingeführt. Ameisen sind eusoziale Insekten, die lieber in der Gemeinschaft überleben und sich erhalten als als einzelne Arten. Sie kommunizieren miteinander über Geräusche, Berührungen und Pheromone. Pheromone sind organische chemische Verbindungen, die von Ameisen abgesondert werden und bei Mitgliedern derselben Art eine soziale Reaktion auslösen. Hierbei handelt es sich um Chemikalien, die wie Hormone außerhalb des Körpers des absondernden Individuums wirken und das Verhalten des empfangenden Individuums beeinflussen können. Da die meisten Ameisen am Boden leben, nutzen sie die Bodenoberfläche, um Pheromonspuren zu hinterlassen, die von anderen Ameisen verfolgt (gerochen) werden können.
Ameisen leben in Gemeinschaftsnestern und das Grundprinzip von ACO besteht darin, die Bewegung der Ameisen aus ihren Nestern zu beobachten, um auf dem kürzesten möglichen Weg nach Nahrung zu suchen. Zunächst bewegen sich Ameisen wahllos auf der Suche nach Nahrung um ihre Nester herum. Diese zufällige Suche eröffnet mehrere Wege vom Nest zur Nahrungsquelle. Abhängig von der Qualität und Quantität der Nahrung transportieren Ameisen nun einen Teil der Nahrung mit der erforderlichen Pheromonkonzentration auf ihrem Rückweg zurück. Abhängig von diesen Pheromonversuchen wäre die Wahrscheinlichkeit, dass die folgenden Ameisen einen bestimmten Weg wählen, ein entscheidender Faktor für die Nahrungsquelle. Offensichtlich basiert diese Wahrscheinlichkeit auf der Konzentration sowie der Verdunstungsrate des Pheromons. Es kann auch beobachtet werden, dass die Länge jedes Pfads leicht erklärt werden kann, da auch die Verdunstungsrate des Pheromons ein entscheidender Faktor ist.

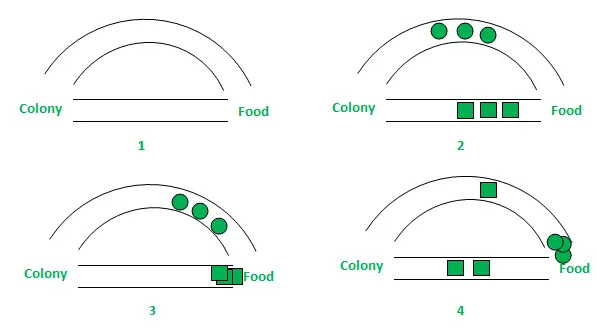
In der obigen Abbildung wurden der Einfachheit halber nur zwei mögliche Wege zwischen der Nahrungsquelle und dem Ameisennest berücksichtigt. Die Phasen können wie folgt analysiert werden:

int in String Java umwandeln

Stufe 1: Alle Ameisen sind in ihrem Nest. Es gibt keinen Pheromongehalt in der Umwelt. (Beim algorithmischen Design kann die verbleibende Pheromonmenge berücksichtigt werden, ohne die Wahrscheinlichkeit zu beeinträchtigen.) Stufe 2: Ameisen beginnen ihre Suche mit der gleichen Wahrscheinlichkeit (jeweils 0,5) auf jedem Weg. Offensichtlich ist der gekrümmte Weg länger und daher benötigen die Ameisen mehr Zeit, um die Nahrungsquelle zu erreichen als bei anderen. Stufe 3: Die Ameisen gelangen über den kürzeren Weg früher zur Nahrungsquelle. Jetzt stehen sie offensichtlich vor einem ähnlichen Selektionsdilemma, aber dieses Mal ist die Selektionswahrscheinlichkeit aufgrund der Pheromonspur entlang des bereits verfügbaren kürzeren Weges höher. Stufe 4: Auf dem kürzeren Weg kehren mehr Ameisen zurück und in der Folge steigen auch die Pheromonkonzentrationen. Darüber hinaus verringert sich aufgrund der Verdunstung die Pheromonkonzentration auf dem längeren Weg, wodurch die Wahrscheinlichkeit einer Selektion dieses Weges in weiteren Stufen sinkt. Daher nutzt die gesamte Kolonie bei höheren Wahrscheinlichkeiten nach und nach den kürzeren Weg. Somit wird eine Pfadoptimierung erreicht.

Algorithmisches Design:

Bezogen auf das oben beschriebene Verhalten der Ameisen kann nun ein algorithmisches Design entwickelt werden. Der Einfachheit halber wurden eine einzelne Nahrungsquelle und eine einzelne Ameisenkolonie mit nur zwei möglichen Durchquerungspfaden betrachtet. Das gesamte Szenario kann durch gewichtete Diagramme realisiert werden, in denen die Ameisenkolonie und die Nahrungsquelle als Eckpunkte (oder Knoten) fungieren. Die Pfade dienen als Kanten und die Pheromonwerte sind die mit den Kanten verbundenen Gewichte.
Lass den Graphen sein G = (V, E) wobei V, E die Kanten und Eckpunkte des Graphen sind. Die Eckpunkte laut unserer Betrachtung sind IN_S (Quellenscheitelpunkt – Ameisenkolonie) und IN_D (Zielscheitelpunkt – Nahrungsquelle), Die beiden Kanten sind UND₁ Und UND₂ mit Längen L₁ Und L₂ jedem zugeordnet. Nun kann davon ausgegangen werden, dass die damit verbundenen Pheromonwerte (die ihre Stärke anzeigen) gleich sind R₁ Und R₂ für Eckpunkte E₁und E₂jeweils. Somit ist für jede Ameise die Anfangswahrscheinlichkeit der Pfadauswahl (zwischen E₁und E₂) kann wie folgt ausgedrückt werden:

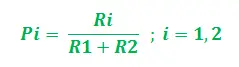
Offensichtlich, wenn R₁>R₂, die Wahrscheinlichkeit, E zu wählen₁ist höher und umgekehrt. Während wir nun auf diesem kürzesten Weg zurückkehren, sagen wir E_ich, wird der Pheromonwert für den entsprechenden Pfad aktualisiert. Die Aktualisierung erfolgt anhand der Länge der Pfade sowie der Verdunstungsrate des Pheromons. Das Update kann also schrittweise wie folgt durchgeführt werden:

Je nach Weglänge –

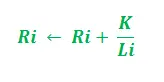
In der obigen Aktualisierung ist i = 1, 2 und „K“ dient als Parameter des Modells. Darüber hinaus ist die Aktualisierung von der Länge des Pfades abhängig. Je kürzer der Weg, desto höher die hinzugefügte Pheromonmenge. Entsprechend der Verdunstungsrate des Pheromons –

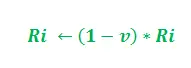
Der Parameter „v“ gehört zum Intervall (0, 1], das die Pheromonverdunstung reguliert. Außerdem ist i = 1, 2.

Bei jeder Iteration werden alle Ameisen am Quellscheitelpunkt V platziert_S(Ameisenkolonie). Anschließend bewegen sich Ameisen von V_Szu V_D(Nahrungsquelle) nach Schritt 1. Als nächstes führen alle Ameisen ihre Rückreise durch und bekräftigen ihren gewählten Weg basierend auf Schritt 2.

Pseudocode:

 Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>

Die Pheromonaktualisierung und die Fitnessberechnungen im obigen Pseudocode können durch die oben erwähnten schrittweisen Implementierungen ermittelt werden.
Somit wurde die Einführung der ACO-Optimierungstechnik etabliert. Die Anwendung des ACO kann auf verschiedene Probleme wie das berühmte ausgeweitet werden TSP (Travelling-Salesman-Problem) .

Verweise:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf