Ist jedes Rechteck eine Raute? Ein Rechteck ist eine zweidimensionale geometrische Figur, die durch vier Seiten und vier Ecken dargestellt wird. Ein Rechteck enthält Seiten, bei denen die Länge der gegenüberliegenden Seiten gleich ist und diese Seiten parallel zueinander sind. Die Seiten teilen sich eine Ecke benachbarter Seiten mit einem Winkel von 90° zwischen ihnen. Daher gibt es im Rechteck vier rechte Winkel.

Inhaltsverzeichnis
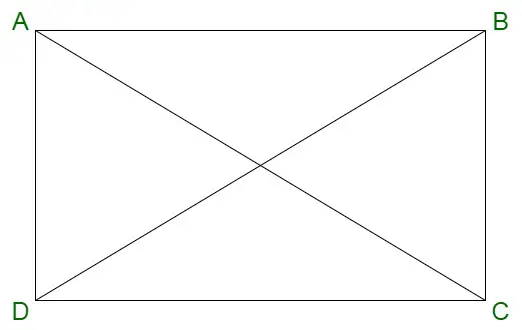
Rechteck
Die Eigenschaften eines Rechtecks sind unten angegeben:
- Es hat vier Kanten und vier Ecken, die sogenannten Eckpunkte.
- Die Diagonalen eines Rechtecks halbieren einander.
- Die Fläche eines Rechtecks entspricht dem Produkt aus Länge und Breite.
- Jeder Scheitelpunkt hat einen Winkel von 90Ö
- Die gegenüberliegenden Seiten eines Rechtecks sind gleich und parallel zueinander.
- Der Umfang entspricht dem Doppelten der Summe seiner Länge und Breite.
- Die Summe aller Innenwinkel beträgt 360 Grad
Umfang eines Rechtecks
Die gesamte Verschiebung, die durch die Grenze des Rechtecks zurückgelegt wird, kann als Umfang bezeichnet werden. Da sowohl Länge als auch Breite als Längeneinheit angegeben werden, wird auch der Umfang in Längeneinheiten gemessen.
Der Umfang kann angegeben werden durch:
Umfang, P = 2 (Länge + Breite)
Fläche des Rechtecks
Der von einer zweidimensionalen geometrischen Figur in einer Ebene abgedeckte Bereich wird als Fläche einer Figur bezeichnet. Somit ist die Fläche eines Rechtecks die Fläche, die innerhalb seiner Grenzen liegt. Es wird in Quadrateinheiten gemessen. Die Fläche entspricht dem Produkt aus Länge und Breite des Rechtecks.
Fläche kann bezeichnet werden durch:
Fläche, A = Länge × Breite in Quadrateinheiten
Diagonale einer Rechteckformel
Diagonalen jeder geometrischen Figur verbinden abwechselnde Eckpunkte. Die Länge der Diagonalen eines Rechtecks kann mit der folgenden Formel berechnet werden, die mit d bezeichnet wird:
d = sqrt{( l^2 + w^2)} Wo,
l = Länge des Rechtecks
w = Breite des Rechtecks
Lesen Sie im Detail: Eigenschaften von Rechtecken: Definition, Formeln, Beispiele
Rhombus
Eine Raute wird auch als vierseitiges Viereck bezeichnet. Es handelt sich um einen Sonderfall eines Parallelogramms. Eine Raute enthält parallele gegenüberliegende Seiten und gleiche gegenüberliegende Winkel. Eine Raute ist auch unter der Bezeichnung Raute oder Rautenraute bekannt. Eine Raute enthält alle Seiten einer Raute, die gleich lang sind. Außerdem halbieren sich die Diagonalen einer Raute im rechten Winkel.
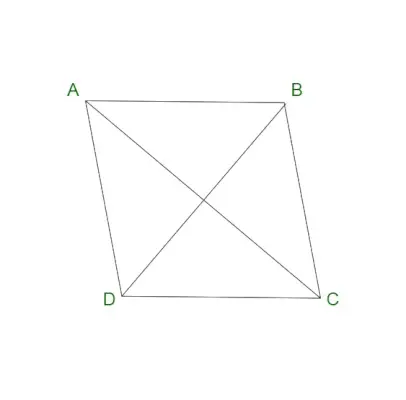
Eigenschaften einer Raute
Eine Raute enthält die folgenden Eigenschaften:
- Eine Raute enthält alle gleichen Seiten.
- Die Diagonalen einer Raute halbieren einander im rechten Winkel.
- Die gegenüberliegenden Seiten einer Raute sind ihrer Natur nach parallel.
- Die Summe zweier benachbarter Winkel einer Raute beträgt 180Ö.
- Innerhalb einer Raute gibt es keinen Beschriftungskreis.
- Es gibt keinen umschreibenden Kreis um eine Raute.
- Die Diagonalen einer Raute führen zur Bildung von vier rechtwinkligen Dreiecken.
- Diese Dreiecke sind zueinander kongruent.
- Die entgegengesetzten Winkel einer Raute sind gleich.
- Wenn man die Mittelpunkte der Seiten einer Raute verbindet, entsteht ein Rechteck.
- Wenn die Mittelpunkte der halben Diagonale verbunden werden, entsteht eine weitere Raute.
Umfang der Raute
Der Umfang einer Raute ist definiert als die Gesamtlänge ihrer Ränder, die die Figur bilden. Es kann auch als Gesamtsumme der Länge von vier Seiten einer Raute bezeichnet werden. Der Umfang einer Raute ist definiert durch:
Umfang, P = 4a Einheiten
wobei die Diagonalen der Raute mit d bezeichnet werden1& D2und „a“ ist die Seite.
Bereich der Raute
Die Fläche der Raute ist definiert als der von einer zweidimensionalen Ebene umschlossene Bereich. Die Fläche einer Raute entspricht dem Produkt der Diagonalen der Raute dividiert durch 2. Die Fläche der Raute kann durch die folgende Formel definiert werden:
Fläche, A =
frac{(d_1 imes d_2)}{2} Quadrateinheitenwo d1und d2sind die Diagonalen einer Raute.
Wir können leicht erkennen, dass jede Raute ein Parallelogramm ist, aber das Gegenteil ist nicht der Fall. Ein Quadrat kann als Sonderfall einer Raute betrachtet werden, da es vier gleich lange Seiten enthält. Ein Quadrat hat alle rechten Winkel. Allerdings sind nicht alle Winkel einer Raute unbedingt rechte Winkel . Zusammenfassend lässt sich sagen, dass eine Raute, die rechte Winkel enthält, als Quadrat betrachtet werden kann. Daher können wir sagen,
- Alle Rauten sind Parallelogramme.
- Alle Parallelogramme sind keine Rauten.
- Nicht alle Rauten sind Quadrate.
- Alle Quadrate sind Rauten.
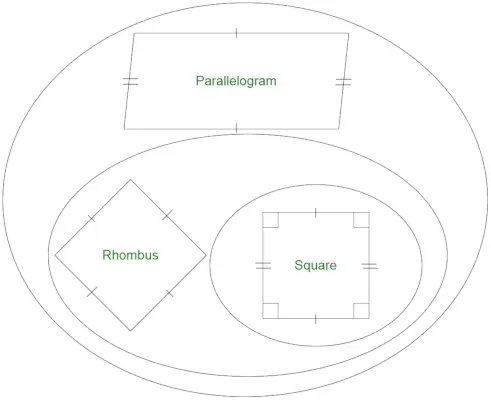
Ist jedes Rechteck eine Raute?
Ein Rechteck ist eine geometrische Figur, die nicht alle gleichen Seiten hat. Ein Quadrat ist ein Sonderfall eines Rechtecks mit allen gleichen Seiten. Denn wir wissen, dass eine Raute alle gleiche Seiten hat. Die Mengen der Rechtecke und Rauten schneiden sich nur bei Quadraten. Daher ist das Rechteck keine Raute.
was ist awt

Warum ist eine Raute ein Rechteck?
Eine Raute ist ein Sonderfall eines Rechtecks. Denn wir wissen, dass sich die Diagonalen einer Raute in gleichen Winkeln schneiden, während die Diagonalen eines Rechtecks gleich lang sind. Durch die Verbindung der Mittelpunkte der Seiten einer Raute entsteht ein Rechteck.
Weiterlesen: Warum ist eine Raute kein Quadrat?
Beispielfragen – Ist jedes Rechteck eine Raute?
Frage 1. Berechnen Sie die Fläche eines rechteckigen Rahmens mit 6 Zoll Zoll Länge und ist 3 Zoll breit.
Lösung:
Denn wir wissen,
Fläche eines Rechtecks = (Länge × Breite) Quadrateinheiten.
Durch Ersetzen der Werte erhalten wir:
die Fläche des rechteckigen Rahmens = 6 × 3 = 18 Quadratzoll
Frage 2: Ermitteln Sie die Länge der Diagonale eines Rechtecks mit einer Länge von 12 cm und einer Breite von 8 cm.
Lösung:
Wir wissen,
Diagonale Länge,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Frage 3. Finden Sie die Fläche einer Raute mit den beiden Diagonallängen d 1 und d 2 6 cm bzw. 12 cm betragen.
Lösung:
Wir haben,
Diagonale d1= 6cm
Diagonale d2= 12 cm
Die Fläche der Raute ist gegeben durch:
A =
frac{(d_1 imes d_2)}{2} QuadrateinheitenA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Daher beträgt die Fläche der Raute 36 cm2.
Frage 4. Unterschied zwischen Raute und Rechteck?
Lösung:
| Eigentum | Rhombus | Rechteck |
| Seiten | Gleiche Seiten. | Gegenüberliegende Seiten sind gleich. |
| Diagonalen | Die Diagonalen halbieren einander im Winkel von 90°. Diagonalen bilden in der Mitte rechte Winkel. | Die Diagonalen halbieren einander in unterschiedlichen Winkeln. Ein Winkel ist ein stumpfer Winkel und der andere ist ein spitzer Winkel. Diagonalen bilden in der Mitte unterschiedliche Winkel – einen stumpfen Winkel und einen spitzen Winkel. |
| Winkel | Gegenüberliegende Winkel sind gleich. Benachbarte Winkel addieren sich zu 180°. | Gegenüberliegende und benachbarte Winkel sind gleich. Der Winkel, den die benachbarten Seiten eines Rechtecks bilden, beträgt 90°. |
