Logistische Regression ist ein überwachter Algorithmus für maschinelles Lernen benutzt für Klassifizierungsaufgaben Dabei besteht das Ziel darin, die Wahrscheinlichkeit vorherzusagen, dass eine Instanz zu einer bestimmten Klasse gehört oder nicht. Die logistische Regression ist ein statistischer Algorithmus, der die Beziehung zwischen zwei Datenfaktoren analysiert. Der Artikel untersucht die Grundlagen der logistischen Regression, ihre Typen und Implementierungen.

Inhaltsverzeichnis

• Was ist logistische Regression?
• Logistische Funktion – Sigmoidfunktion
• Arten der logistischen Regression
• Annahmen der logistischen Regression
• Wie funktioniert die logistische Regression?
• Code-Implementierung für die logistische Regression
• Präzisions-Rückruf-Kompromiss bei der Schwellenwerteinstellung für die logistische Regression
• Wie bewertet man das logistische Regressionsmodell?
• Unterschiede zwischen linearer und logistischer Regression

Was ist logistische Regression?

Für Binärdaten wird die logistische Regression verwendet Einstufung wo wir verwenden Sigmoidfunktion , das Eingaben als unabhängige Variablen annimmt und einen Wahrscheinlichkeitswert zwischen 0 und 1 erzeugt.

Wir haben zum Beispiel zwei Klassen: Klasse 0 und Klasse 1. Wenn der Wert der Logistikfunktion für eine Eingabe größer als 0,5 (Schwellenwert) ist, dann gehört sie zur Klasse 1, andernfalls gehört sie zur Klasse 0. Man spricht deshalb von Regression ist die Erweiterung von lineare Regression wird aber hauptsächlich für Klassifizierungsprobleme verwendet.

Wichtige Punkte:

• Die logistische Regression sagt die Ausgabe einer kategorialen abhängigen Variablen voraus. Daher muss das Ergebnis ein kategorialer oder diskreter Wert sein.
• Es kann entweder „Ja“ oder „Nein“, „0“ oder „1“, „wahr“ oder „falsch“ usw. sein. Anstatt jedoch den genauen Wert als 0 und 1 anzugeben, werden die Wahrscheinlichkeitswerte angegeben, die zwischen 0 und 1 liegen.
• Bei der logistischen Regression passen wir statt einer Regressionsgerade eine S-förmige Logistikfunktion an, die zwei Maximalwerte (0 oder 1) vorhersagt.

Logistische Funktion – Sigmoidfunktion

• Die Sigmoidfunktion ist eine mathematische Funktion, mit der die vorhergesagten Werte auf Wahrscheinlichkeiten abgebildet werden.
• Es bildet jeden realen Wert in einen anderen Wert innerhalb eines Bereichs von 0 und 1 ab. Der Wert der logistischen Regression muss zwischen 0 und 1 liegen und darf diese Grenze nicht überschreiten, sodass eine Kurve wie die S-Form entsteht.
• Die S-förmige Kurve wird Sigmoidfunktion oder logistische Funktion genannt.
• Bei der logistischen Regression verwenden wir das Konzept des Schwellenwerts, der die Wahrscheinlichkeit von entweder 0 oder 1 definiert. Werte über dem Schwellenwert tendieren beispielsweise zu 1 und ein Wert unter den Schwellenwerten tendiert zu 0.

Arten der logistischen Regression

Auf der Grundlage der Kategorien kann die logistische Regression in drei Typen eingeteilt werden:

1. Binomial: Bei der binomialen logistischen Regression kann es nur zwei mögliche Typen abhängiger Variablen geben, z. B. 0 oder 1, Bestanden oder Nicht bestanden usw.
2. Multinomial: Bei der multinomialen logistischen Regression kann es drei oder mehr mögliche ungeordnete Typen der abhängigen Variablen geben, z. B. Katze, Hunde oder Schaf
3. Ordinal: Bei der ordinalen logistischen Regression kann es drei oder mehr mögliche geordnete Typen abhängiger Variablen geben, z. B. niedrig, mittel oder hoch.

Annahmen der logistischen Regression

Wir werden die Annahmen der logistischen Regression untersuchen, da das Verständnis dieser Annahmen wichtig ist, um sicherzustellen, dass wir das Modell angemessen anwenden. Die Annahme umfasst:

1. Unabhängige Beobachtungen: Jede Beobachtung ist unabhängig von der anderen. Dies bedeutet, dass zwischen den Eingabevariablen keine Korrelation besteht.
2. Binäre abhängige Variablen: Es wird davon ausgegangen, dass die abhängige Variable binär oder dichotom sein muss, was bedeutet, dass sie nur zwei Werte annehmen kann. Für mehr als zwei Kategorien werden SoftMax-Funktionen verwendet.
3. Linearitätsbeziehung zwischen unabhängigen Variablen und logarithmischen Quoten: Die Beziehung zwischen den unabhängigen Variablen und den logarithmischen Quoten der abhängigen Variablen sollte linear sein.
4. Keine Ausreißer: Der Datensatz sollte keine Ausreißer enthalten.
5. Große Stichprobengröße: Die Stichprobengröße ist ausreichend groß

Terminologien im Zusammenhang mit der logistischen Regression

Hier sind einige gebräuchliche Begriffe für die logistische Regression:

• Unabhängige Variablen: Die Eingabemerkmale oder Prädiktorfaktoren, die auf die Vorhersagen der abhängigen Variablen angewendet werden.
• Abhängige Variable: Die Zielvariable in einem logistischen Regressionsmodell, die wir vorhersagen möchten.
• Logistikfunktion: Die Formel, die verwendet wird, um darzustellen, wie sich die unabhängigen und abhängigen Variablen zueinander verhalten. Die Logistikfunktion wandelt die Eingabevariablen in einen Wahrscheinlichkeitswert zwischen 0 und 1 um, der die Wahrscheinlichkeit darstellt, dass die abhängige Variable 1 oder 0 ist.
• Chancen: Es ist das Verhältnis von etwas, das geschieht, zu etwas, das nicht geschieht. Sie unterscheidet sich von der Wahrscheinlichkeit, da die Wahrscheinlichkeit das Verhältnis von etwas, das passiert, zu allem, was möglicherweise passieren könnte, ist.
• Log-Quoten: Die Log-Quoten, auch Logit-Funktion genannt, sind der natürliche Logarithmus der Quoten. Bei der logistischen Regression werden die logarithmischen Quoten der abhängigen Variablen als lineare Kombination der unabhängigen Variablen und des Achsenabschnitts modelliert.
• Koeffizient: Die geschätzten Parameter des logistischen Regressionsmodells zeigen, wie sich die unabhängigen und abhängigen Variablen zueinander verhalten.
• Abfangen: Ein konstanter Term im logistischen Regressionsmodell, der die logarithmischen Quoten darstellt, wenn alle unabhängigen Variablen gleich Null sind.
• Maximum-Likelihood-Schätzung : Die zur Schätzung der Koeffizienten des logistischen Regressionsmodells verwendete Methode, die die Wahrscheinlichkeit der Beobachtung der vom Modell gegebenen Daten maximiert.

Wie funktioniert die logistische Regression?

Das logistische Regressionsmodell transformiert die lineare Regression Funktion kontinuierliche Wertausgabe in kategoriale Wertausgabe mithilfe einer Sigmoidfunktion, die jeden reellwertigen Satz unabhängiger Variableneingabe in einen Wert zwischen 0 und 1 abbildet. Diese Funktion wird als logistische Funktion bezeichnet.

Die unabhängigen Eingabemerkmale seien:

X = egin{bmatrix} x_{11} & … & x_{1m} x_{21} & … & x_{2m} vdots & ddots & vdots x_{n1} & … & x_{nm} end{bmatrix}

und die abhängige Variable ist Y, die nur einen binären Wert hat, d. h. 0 oder 1.

Y = egin{cases} 0 & ext{ if } Class;1 1 & ext{ if } Class;2 end{cases}

Wenden Sie dann die multilineare Funktion auf die Eingabevariablen X an.

z = left(sum_{i=1}^{n} w_{i}x_{i} ight) + b

Hierx_i ist die i-te Beobachtung von X,w_i = [w_1, w_2, w_3, cdots,w_m] ist die Gewichtung oder der Koeffizient und b ist der Bias-Term, der auch als Achsenabschnitt bezeichnet wird. Dies kann einfach als Skalarprodukt aus Gewicht und Bias dargestellt werden.

z = wcdot X +b

Was auch immer wir oben besprochen haben, ist das lineare Regression .

Sigmoidfunktion

Jetzt verwenden wir die Sigmoidfunktion wobei die Eingabe z ist und wir die Wahrscheinlichkeit zwischen 0 und 1 finden, d. h. das vorhergesagte y.

sigma(z) = frac{1}{1-e^{-z}}

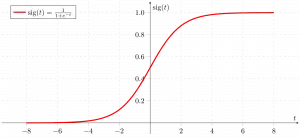
Sigmoidfunktion

Wie oben gezeigt, wandelt die Sigmoidfunktion die kontinuierlichen Variablendaten in um Wahrscheinlichkeit also zwischen 0 und 1.

Android-Entwicklermodus ausschalten

• sigma(z) tendiert zu 1 asz ightarrowinfty
• sigma(z) tendiert gegen 0 asz ightarrow-infty
• sigma(z) ist immer zwischen 0 und 1 begrenzt

wobei die Wahrscheinlichkeit, eine Klasse zu sein, wie folgt gemessen werden kann:

P(y=1) = sigma(z) P(y=0) = 1-sigma(z)

Logistische Regressionsgleichung

Die Odds ist das Verhältnis von etwas, das passiert, zu etwas, das nicht passiert. Sie unterscheidet sich von der Wahrscheinlichkeit, da die Wahrscheinlichkeit das Verhältnis von etwas, das passiert, zu allem, was möglicherweise passieren könnte, ist. so seltsam wird sein:

frac{p(x)}{1-p(x)} = e^z

Anwenden von natürlichem Protokoll auf ungerade. dann ist log odd:

egin{aligned} log left[frac{p(x)}{1-p(x)} ight] &= z log left[frac{p(x)}{1-p(x)} ight] &= wcdot X +b frac{p(x)}{1-p(x)}&= e^{wcdot X +b} ;;cdots ext{Exponentiate both sides} p(x) &=e^{wcdot X +b}cdot (1-p(x)) p(x) &=e^{wcdot X +b}-e^{wcdot X +b}cdot p(x)) p(x)+e^{wcdot X +b}cdot p(x))&=e^{wcdot X +b} p(x)(1+e^{wcdot X +b}) &=e^{wcdot X +b} p(x)&= frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} end{aligned}

dann lautet die endgültige logistische Regressionsgleichung:

p(X;b,w) = frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} = frac{1}{1+e^{-wcdot X +b}}

Wahrscheinlichkeitsfunktion für die logistische Regression

Die vorhergesagten Wahrscheinlichkeiten sind:

• für y=1 Die vorhergesagten Wahrscheinlichkeiten sind: p(X;b,w) = p(x)
• für y = 0 Die vorhergesagten Wahrscheinlichkeiten sind: 1-p(X;b,w) = 1-p(x)

L(b,w) = prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}

Beidseitige Aufnahme von Naturstämmen

egin{aligned}log(L(b,w)) &= sum_{i=1}^{n} y_ilog p(x_i);+; (1-y_i)log(1-p(x_i)) &=sum_{i=1}^{n} y_ilog p(x_i)+log(1-p(x_i))-y_ilog(1-p(x_i)) &=sum_{i=1}^{n} log(1-p(x_i)) +sum_{i=1}^{n}y_ilog frac{p(x_i)}{1-p(x_i} &=sum_{i=1}^{n} -log1-e^{-(wcdot x_i+b)} +sum_{i=1}^{n}y_i (wcdot x_i +b) &=sum_{i=1}^{n} -log1+e^{wcdot x_i+b} +sum_{i=1}^{n}y_i (wcdot x_i +b) end{aligned}

Gradient der Log-Likelihood-Funktion

Um die Maximum-Likelihood-Schätzungen zu finden, differenzieren wir nach w.r.t.

egin{aligned} frac{partial J(l(b,w)}{partial w_j}&=-sum_{i=n}^{n}frac{1}{1+e^{wcdot x_i+b}}e^{wcdot x_i+b} x_{ij} +sum_{i=1}^{n}y_{i}x_{ij} &=-sum_{i=n}^{n}p(x_i;b,w)x_{ij}+sum_{i=1}^{n}y_{i}x_{ij} &=sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} end{aligned}

Code-Implementierung für die logistische Regression

Binomiale logistische Regression:

Die Zielvariable kann nur zwei mögliche Typen haben: 0 oder 1, was Sieg vs. Niederlage, Bestanden vs. Misserfolg, tot vs. lebendig usw. darstellen kann. In diesem Fall werden Sigmoidfunktionen verwendet, was oben bereits erläutert wurde.

Importieren notwendiger Bibliotheken basierend auf den Anforderungen des Modells. Dieser Python-Code zeigt, wie der Brustkrebsdatensatz verwendet wird, um ein logistisches Regressionsmodell zur Klassifizierung zu implementieren.

Ausgabe :

Genauigkeit des logistischen Regressionsmodells (in %): 95,6140350877193

Multinomiale logistische Regression:

Die Zielvariable kann drei oder mehr mögliche Typen haben, die nicht geordnet sind (d. h. Typen haben keine quantitative Bedeutung), wie Krankheit A vs. Krankheit B vs. Krankheit C.

In diesem Fall wird die Softmax-Funktion anstelle der Sigmoidfunktion verwendet. Softmax-Funktion für K-Klassen wird sein:

ext{softmax}(z_i) =frac{ e^{z_i}}{sum_{j=1}^{K}e^{z_{j}}}

Hier, K stellt die Anzahl der Elemente im Vektor z dar und i, j iteriert über alle Elemente im Vektor.

Dann ist die Wahrscheinlichkeit für Klasse c:

P(Y=c | overrightarrow{X}=x) = frac{e^{w_c cdot x + b_c}}{sum_{k=1}^{K}e^{w_k cdot x + b_k}}

Bei der multinomialen logistischen Regression kann die Ausgabevariable Folgendes haben: mehr als zwei mögliche diskrete Ausgänge . Betrachten Sie den Zifferndatensatz.

Ausgabe:

Genauigkeit des logistischen Regressionsmodells (in %): 96,52294853963839

Wie bewertet man das logistische Regressionsmodell?

Wir können das logistische Regressionsmodell anhand der folgenden Metriken bewerten:

sts herunterladen

• Genauigkeit: Genauigkeit gibt den Anteil korrekt klassifizierter Instanzen an.
  Accuracy = frac{True , Positives + True , Negatives}{Total}

• Präzision: Präzision konzentriert sich auf die Genauigkeit positiver Vorhersagen.
  Precision = frac{True , Positives }{True, Positives + False , Positives}

• Rückruf (Sensitivität oder True-Positive-Rate): Abrufen misst den Anteil korrekt vorhergesagter positiver Instanzen an allen tatsächlichen positiven Instanzen.
  Recall = frac{ True , Positives}{True, Positives + False , Negatives}

• F1-Ergebnis: F1-Ergebnis ist das harmonische Mittel von Präzision und Erinnerung.
  F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}

• Fläche unter der Receiver Operating Characteristic Curve (AUC-ROC): Die ROC-Kurve stellt die Richtig-Positiv-Rate gegenüber der Falsch-Positiv-Rate bei verschiedenen Schwellenwerten dar. AUC-ROC misst die Fläche unter dieser Kurve und liefert so ein aggregiertes Maß für die Leistung eines Modells über verschiedene Klassifizierungsschwellen hinweg.
• Fläche unter der Precision-Recall-Kurve (AUC-PR): Ähnlich wie AUC-ROC, AUC-PR misst die Fläche unter der Precision-Recall-Kurve und liefert eine Zusammenfassung der Leistung eines Modells über verschiedene Precision-Recall-Kompromisse hinweg.

Präzisions-Rückruf-Kompromiss bei der Schwellenwerteinstellung für die logistische Regression

Die logistische Regression wird nur dann zu einer Klassifizierungstechnik, wenn eine Entscheidungsschwelle ins Spiel kommt. Die Festlegung des Schwellenwerts ist ein sehr wichtiger Aspekt der logistischen Regression und hängt vom Klassifizierungsproblem selbst ab.

Die Entscheidung über den Wert des Schwellenwerts wird maßgeblich von den Werten von beeinflusst Präzision und Erinnerung. Idealerweise möchten wir, dass sowohl Präzision als auch Erinnerung 1 sind, aber das ist selten der Fall.

Im Falle eines Kompromiss zwischen Präzision und Rückruf verwenden wir die folgenden Argumente, um über den Schwellenwert zu entscheiden:

1. Geringe Präzision/hoher Rückruf: In Anwendungen, in denen wir die Anzahl falsch-negativer Ergebnisse reduzieren möchten, ohne unbedingt die Anzahl falsch-positiver Ergebnisse zu verringern, wählen wir einen Entscheidungswert mit einem niedrigen Präzisionswert oder einem hohen Recall-Wert. Beispielsweise möchten wir bei einem Krebsdiagnoseantrag nicht, dass ein betroffener Patient als nicht betroffen eingestuft wird, ohne große Rücksicht darauf zu nehmen, ob bei dem Patienten fälschlicherweise Krebs diagnostiziert wird. Dies liegt daran, dass das Fehlen von Krebs zwar durch weitere medizinische Erkrankungen nachgewiesen werden kann, das Vorliegen der Erkrankung jedoch bei einem bereits abgelehnten Kandidaten nicht nachgewiesen werden kann.
2. Hohe Präzision/geringer Rückruf: In Anwendungen, in denen wir die Anzahl der falsch-positiven Ergebnisse reduzieren möchten, ohne unbedingt die Anzahl der falsch-negativen Ergebnisse zu verringern, wählen wir einen Entscheidungswert mit einem hohen Präzisionswert oder einem niedrigen Recall-Wert. Wenn wir beispielsweise Kunden danach klassifizieren, ob sie positiv oder negativ auf eine personalisierte Werbung reagieren, möchten wir absolut sicher sein, dass der Kunde positiv auf die Werbung reagiert, da andernfalls eine negative Reaktion zu potenziellen Umsatzeinbußen führen kann Kunde.

Unterschiede zwischen linearer und logistischer Regression

Der Unterschied zwischen linearer Regression und logistischer Regression besteht darin, dass die Ausgabe der linearen Regression der kontinuierliche Wert ist, der alles sein kann, während die logistische Regression die Wahrscheinlichkeit vorhersagt, dass eine Instanz zu einer bestimmten Klasse gehört oder nicht.

Logistische Regression – Häufig gestellte Fragen (FAQs)

Was ist logistische Regression beim maschinellen Lernen?

Die logistische Regression ist eine statistische Methode zur Entwicklung von Modellen für maschinelles Lernen mit binär abhängigen Variablen, also binär. Die logistische Regression ist eine statistische Technik zur Beschreibung von Daten und der Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen.

Welche drei Arten der logistischen Regression gibt es?

Die logistische Regression wird in drei Typen eingeteilt: binär, multinomial und ordinal. Sie unterscheiden sich sowohl in der Ausführung als auch in der Theorie. Bei der binären Regression geht es um zwei mögliche Ergebnisse: Ja oder Nein. Die multinomiale logistische Regression wird verwendet, wenn drei oder mehr Werte vorhanden sind.

Warum wird die logistische Regression für Klassifizierungsprobleme verwendet?

Die logistische Regression ist einfacher zu implementieren, zu interpretieren und zu trainieren. Es klassifiziert unbekannte Datensätze sehr schnell. Wenn der Datensatz linear trennbar ist, ist die Leistung gut. Modellkoeffizienten können als Indikatoren für die Wichtigkeit von Merkmalen interpretiert werden.

Was unterscheidet die logistische Regression von der linearen Regression?

Während die lineare Regression zur Vorhersage kontinuierlicher Ergebnisse verwendet wird, wird die logistische Regression verwendet, um die Wahrscheinlichkeit vorherzusagen, mit der eine Beobachtung in eine bestimmte Kategorie fällt. Die logistische Regression verwendet eine S-förmige Logistikfunktion, um vorhergesagte Werte zwischen 0 und 1 abzubilden.

Welche Rolle spielt die Logistikfunktion bei der logistischen Regression?

Die logistische Regression basiert auf der logistischen Funktion, um die Ausgabe in einen Wahrscheinlichkeitswert umzuwandeln. Dieser Wert stellt die Wahrscheinlichkeit dar, dass eine Beobachtung zu einer bestimmten Klasse gehört. Die S-förmige Kurve hilft bei der Schwellenwertermittlung und Kategorisierung von Daten in binäre Ergebnisse.