Es gibt zahlreiche Möglichkeiten, die Leistung eines Klassifikators zu bewerten. In diesem Artikel stellen wir die Precision-Recall-Kurve vor und untersuchen den Unterschied zwischen zwei gängigen Leistungsberichtsmethoden weiter: Precision-Recall (PR) Curve und Betriebscharakteristik des Empfängers (ROC) Kurve. Die ROC-Kurve wird bereits im besprochen Artikel . Lassen Sie uns kurz verstehen, was eine Precision-Recall-Kurve ist.
Zeichenfolge im Array in c
Was ist Präzision und Rückruf?
Präzision
- Das Verhältnis der korrekt vorhergesagten positiven Beobachtungen zu allen vorhergesagten positiven Beobachtungen wird als Präzision bezeichnet.
- Es misst, wie gut das Modell die positiven Ergebnisse vorhersagt.
- Die Präzisionsformel lautet:
- Bei der Präzision geht es um die Qualität positiver Vorhersagen. Eine hohe Präzision zeigt an, dass das Modell eine geringe Rate falsch positiver Ergebnisse aufweist.
Abrufen
- Das Verhältnis der korrekt vorhergesagten positiven Beobachtungen zur Gesamtzahl der tatsächlichen positiven Beobachtungen wird als Erinnerung bezeichnet.
- Es misst, wie gut das Modell jede relevante Instanz erfassen kann.
- Der Rückruf wird mit dieser Formel berechnet:
- Beim Rückruf geht es um die Menge der relevanten Instanzen, die vom Modell erfasst werden. Ein hoher Rückruf weist darauf hin, dass das Modell eine niedrige Rate an falsch-negativen Ergebnissen aufweist.
Im Hinblick auf die empirische Interpretation ist eine Verwirrungsmatrix, die aus vier wesentlichen Begriffen besteht, das nützlichste Werkzeug zum Verständnis von Präzision und Erinnerung:
- True Positive (TP): Die Anzahl der positiven Klasseninstanzen, die genau identifiziert wurden
- False Positive (FP): Die Anzahl negativer Klasseninstanzen, die fälschlicherweise als positive Klasseninstanzen identifiziert werden, wird als False Positive (FP) bezeichnet.
- True Negative (TN): Die Anzahl der negativen Klasseninstanzen, die genau identifiziert wurden
- Falsch Negativ (FN): Anzahl positiver Klasseninstanzen, die fälschlicherweise als negative Klasseninstanzen klassifiziert werden (Falsch Negativ oder FN)
Precision-Recall (PR)-Kurve beim maschinellen Lernen
Präzision ist der Anteil von richtig positive Klassifizierungen (echt positiv) geteilt durch die Gesamtzahl vorhergesagt positive Klassifizierungen, die vorgenommen wurden (richtig positiv + falsch positiv). Abrufen ist der Anteil von richtig positive Klassifizierungen (echt positiv) geteilt durch die Gesamtzahl der wirklich positive Klassifizierungen (richtig positiv + falsch negativ).
Eine PR-Kurve ist einfach ein Diagramm mit Präzisionswerten auf der y-Achse und Recall-Werten auf der x-Achse. Mit anderen Worten, die PR-Kurve enthält
- Es ist wichtig zu beachten, dass Präzision auch als positiver Vorhersagewert (PPV) bezeichnet wird.
- Der Rückruf wird auch Sensitivität, Trefferquote oder True Positive Rate (TPR) genannt.
Die folgende Abbildung zeigt einen Vergleich der Beispiel-PR- und ROC-Kurven. 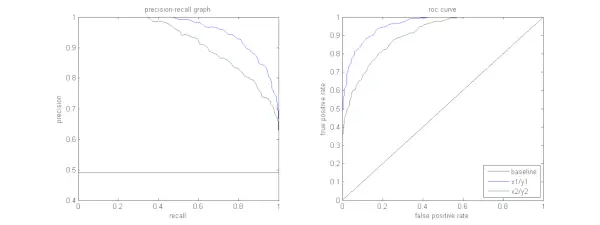
Interpretation einer Precision-Recall-Kurve
Es ist wünschenswert, dass der Algorithmus sowohl eine hohe Präzision als auch einen hohen Rückruf aufweist. Die meisten Algorithmen für maschinelles Lernen erfordern jedoch häufig einen Kompromiss zwischen beiden. Eine gute PR-Kurve hat mehr AUC (Fläche unter der Kurve) . In der Abbildung oben weist der Klassifikator, der der blauen Linie entspricht, eine bessere Leistung auf als der Klassifikator, der der grünen Linie entspricht. Es ist wichtig zu beachten, dass der Klassifikator eine höhere AUC aufweist ROC-Kurve wird auch immer eine höhere AUC auf der PR-Kurve haben. Stellen Sie sich einen Algorithmus vor, der klassifiziert, ob ein Dokument zur Kategorie Sportnachrichten gehört oder nicht. Angenommen, es gibt 12 Dokumente mit den folgenden Grundwahrheits- (tatsächlichen) und Klassifikator-Ausgabeklassenbezeichnungen.
| Dokument Identifikation | Grundwahrheit | Ausgabe des Klassifikators |
|---|---|---|
| D1 | Sport | Sport |
| D2 | Sport | Sport |
| D3 | Nicht Sport | Sport |
| D4 | Sport | Nicht Sport |
| D5 | Nicht Sport | Nicht Sport |
| D6 | Sport | Nicht Sport |
| D7 | Nicht Sport | Sport |
| D8 | Nicht Sport | Nicht Sport |
| D9 | Nicht Sport | Nicht Sport |
| D10 | Sport | Sport |
| D11 | Sport | Sport |
| D12 | Sport | Nicht Sport |
Lassen Sie uns nun die TP-, TN-, FP- und FN-Werte ermitteln.
Lassen Sie uns ein Beispiel mit Dokumenten verwenden, die als Sport oder Nicht-Sport klassifiziert sind, um die Definitionen von True Positives (TP), True Negatives (TN), False Positives (FP) und False Negatives (FN) im Kontext der Klassifizierung besser zu erläutern:
Echte Positive (TP): Dokumente, die genau der Kategorie „Sport“ zugeordnet wurden und in denen es tatsächlich um Sport ging. Die Dokumente D1, D2, D10 und D11 in diesem Szenario sind Instanzen von TP.
Javascript-TutorialEchte Negative (TN): Echte Negative sind die Fälle, in denen das Dokument angemessen als „Kein Sport“ gekennzeichnet wurde, obwohl es nichts mit Sport zu tun hatte. In diesem Fall wird TN durch die Dokumente D5, D8 und D9 nachgewiesen.
Falsch Positive (FP): Dokumente, die fälschlicherweise als Sport eingestuft wurden, obwohl sie nichts mit Sport zu tun hatten. Hier einige FP-Beispiele, Dokumente D3 und D7.
Falsch Negative (FN): Beispiele für Dokumente, die fälschlicherweise als „Kein Sport“ gekennzeichnet waren, sich aber in Wirklichkeit mit Sport befassten. Die Dokumente D4, D6 und D12 sind in diesem Fall FN-Beispiele.
Angesichts dieser Zahlen: Stadt =4, TN =3, FP =2, FN =3
Schließlich werden Präzision und Rückruf wie folgt berechnet:
Precision = frac{TP}{TP+FP} = frac{4}{6} = frac{2}{3}
Recall = frac{TP}{TP+FN} = frac{4}{7} Daraus folgt, dass der Rückruf 4/7 beträgt, wenn die Präzision 2/3 beträgt. Anders ausgedrückt: Von allen als positiv erwarteten Fällen wurden zwei Drittel genau klassifiziert (Präzision) und von allen Fällen, die tatsächlich positiv waren, konnte das Modell vier Siebtel davon erfassen (Recall).
Indem wir unterschiedliche Schwellenwerte festlegen, erhalten wir mehrere solcher Präzisions- und Rückrufpaare. Durch die Darstellung mehrerer solcher P-R-Paare mit Werten zwischen 0 und 1 erhalten wir eine PR-Kurve.
Ist eine PR-Kurve erforderlich, wenn die ROC-Kurve existiert?
Die PR-Kurve ist besonders nützlich bei der Berichterstattung über Ergebnisse des Informationsabrufs.
Beim Informationsabruf wird ein Pool von Dokumenten durchsucht, um Dokumente zu finden, die für eine bestimmte Benutzeranfrage relevant sind. Angenommen, der Benutzer gibt die Suchanfrage „Pink Elephants“ ein. Die Suchmaschine durchsucht Millionen von Dokumenten (mithilfe einiger optimierter Algorithmen), um eine Handvoll relevanter Dokumente abzurufen. Daher können wir mit Sicherheit davon ausgehen, dass die Nr. der relevanten Dokumente wird im Vergleich zur Nr. deutlich geringer ausfallen. von nicht relevanten Dokumenten.
In diesem Szenario,
- TP = Anzahl der abgerufenen Dokumente, die relevant sind (gute Ergebnisse).
- FP = Anzahl der abgerufenen Dokumente, die nicht relevant sind (falsche Suchergebnisse).
- TN = Anzahl der nicht abgerufenen Dokumente, die nicht relevant sind.
- FN = Anzahl der nicht abgerufenen Dokumente, die relevant sind (gute Dokumente, die wir übersehen haben).
Die ROC-Kurve ist ein Diagramm mit Recall = TPR =
Darüber hinaus hilft uns FPR nicht dabei, ein Abrufsystem gut zu bewerten, da wir uns mehr auf die abgerufenen Dokumente konzentrieren möchten und nicht auf die nicht abgerufenen. Die PR-Kurve hilft, dieses Problem zu lösen. Die PR-Kurve hat den Recall-Wert (TPR) auf der x-Achse und die Genauigkeit =
PD-Zusammenführung
Wann sollten ROC- und Precision-Recall-Kurven verwendet werden?
ROC (Receiver Operating Characteristic)-Kurven sind geeignet, wenn die Klassenverteilung ausgeglichen ist und falsch positive und falsch negative Ergebnisse ähnliche Konsequenzen haben. Sie stellen den Kompromiss zwischen Sensitivität und Spezifität dar. Im Gegensatz dazu sind Precision-Recall-Kurven vorzuziehen, wenn es um unausgeglichene Datensätze geht und der Schwerpunkt auf einer positiven Klassenvorhersageleistung liegt.
Precision-Recall bietet Einblicke in die Fähigkeit des Modells, positive Instanzen korrekt zu klassifizieren. Die Wahl zwischen ROC und Precision-Recall hängt von den spezifischen Anforderungen des Problems ab und betont, wie wichtig es ist, die Datenverteilung und die Folgen verschiedener Fehlertypen zu verstehen.
Grundlegende Code-Implementierung für Precision-Recall Curve
Importieren notwendiger Bibliotheken
Diese Codezeilen importieren die Python-Bibliotheken und Module, die zum Generieren einer Präzisionsrückrufkurve erforderlich sind Sci-Kit-Lernen und visualisieren Sie die Ergebnisse mit Matplotlib . Matplotlib ist eine beliebte Python-Plotbibliothek, und pyplot bietet eine unkomplizierte Schnittstelle zum Erstellen verschiedener Arten von Plots und Diagrammen. Logistische Regression ist ein beliebter Klassifizierungsalgorithmus für Binär- und Mehrklassenklassifizierungsaufgaben. Die Precision-Recall-Kurve und die AUC sind beliebte Bewertungsmetriken für binäre Klassifizierung Probleme, insbesondere beim Umgang mit unausgeglichenen Datensätzen.
Python3 import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import precision_recall_curve, auc> Verwendeter Datensatz
Dieser Code generiert einen synthetischen Datensatz für ein binäres Klassifizierungsproblem mithilfe der Funktion „make_classification“ von sci-kit-learn.
Python3 # Generate a synthetic dataset X, y = make_classification( n_samples=1000, n_features=20, n_classes=2, random_state=42)> Trainings- und Test-Split
Der train_test_split Die Funktion in scikit-learn wird in diesem Codeausschnitt verwendet, um den zuvor generierten synthetischen Datensatz (X und Y) in Trainings- und Testsätze aufzuteilen. Diese Aufteilung ist ein entscheidender Schritt bei der Bewertung von Modellen für maschinelles Lernen. Das Modell wird anhand der X_train- und y_train-Daten trainiert, bevor es anhand der X_test- und y_test-Daten getestet wird, um zu sehen, wie gut es bei unsichtbaren Proben funktioniert. Die Funktion train_test_split trennt Trainings- und Testsätze und stellt so sicher, dass die Leistung des Modells seine Verallgemeinerung auf neue, bisher nicht sichtbare Daten widerspiegelt.
Python3 # Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)> Modellbau
Hier verwenden wir die logistische Regression, um das Modell anhand des Trainingsdatensatzes zu trainieren. Die logistische Regression ist ein beliebter Algorithmus für die binäre Klassifizierung und wird von der Sci-Kit-Learn-Klasse LogisticRegression implementiert.
Python3 # Train a logistic regression model (you can replace this with your own classifier) model = LogisticRegression() model.fit(X_train, y_train)> Modellvorhersage
Diese Berechnungen liefern in der Regel Präzisions- und Erinnerungswerte für verschiedene Entscheidungsschwellenwerte, mit denen Sie eine Präzisions-Erinnerungskurve zeichnen oder die relative Bedeutung von Präzision und Erinnerung zu verschiedenen Zeitpunkten untersuchen können. Und die Berechnung der Fläche unter der Kurve (AUC) für die Precision-Recall-Kurve.
Python3 # Predict probabilities for positive class y_scores = model.predict_proba(X_test)[:, 1] # Calculate precision and recall precision, recall, thresholds = precision_recall_curve(y_test, y_scores) # Calculate Area Under the Curve (AUC) for precision-recall curve auc_score = auc(recall, precision)> Zeichnen einer PR-Kurve
Dieser Codeblock bietet eine Standardmethode zur Visualisierung der Präzisions-Rückrufkurve und ermöglicht Ihnen die Bewertung des Kompromisses zwischen Präzision und Rückruf bei verschiedenen Entscheidungsschwellenwerten. Die Gesamtleistung des Modells auf der Precision-Recall-Kurve wird durch den in der Legende angezeigten AUC-Score zusammengefasst.
Python3 # Plot precision-recall curve plt.figure(figsize=(8, 6)) plt.plot(recall, precision, label=f'Precision-Recall Curve (AUC = {auc_score:.2f})') plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall Curve') plt.legend() plt.show()> Ausgabe :
aus CSV-Java lesen

Precision-Recall-Kurve
Häufig gestellte Fragen (FAQs)
F. Was ist Präzision?
Das Verhältnis der genau vorhergesagten positiven Beobachtungen zur Gesamtzahl der vorhergesagten positiven Beobachtungen wird als Präzision bezeichnet. Es misst, wie gut das Modell die positiven Ergebnisse vorhersagt. Das Folgende ist die Präzisionsformel:
Precision = frac{True Positives}{True Positives + False Positives}
F. Was ist Rückruf?
Der Rückruf ist das Verhältnis der korrekt vorhergesagten positiven Beobachtungen zur Gesamtzahl der tatsächlichen positiven Beobachtungen. Sie wird auch als Sensitivität oder echte positive Rate bezeichnet. Dabei wird beurteilt, wie gut das Modell jede relevante Instanz erfassen kann. Der Rückruf wird anhand der folgenden Formel berechnet:
Precision = frac{True Positives}{True Positives + False Negatives} Pawandeep Rajan
F. Warum brauchen wir Präzision und Erinnerung?
Um die Leistung eines Klassifikators bei binären und mehrklassigen Klassifizierungsproblemen zu bewerten, werden zwei Bewertungsmetriken verwendet: Präzision und Rückruf. Die Genauigkeit positiver Vorhersagen wird durch Präzision gemessen, und die Vollständigkeit positiver Vorhersagen wird durch Rückruf gemessen.
F. Was ist der Kompromiss zwischen Rückruf und Präzision?
Erinnerung und Präzision sind häufig Kompromisse. Die Erinnerung kann mit zunehmender Präzision leiden und umgekehrt. Durch Ändern der Messlatte für die Identifizierung einer positiven Instanz kann dieser Kompromiss bewältigt werden. Umgekehrt führt ein niedrigerer Schwellenwert zu einer geringeren Erinnerung, aber höherer Präzision. Die Entscheidung zwischen Rückruf und Präzision basiert auf den Besonderheiten des gegebenen Problems.
F. Was ist der F1-Score und in welcher Beziehung steht er zu Präzision und Erinnerung?
Das harmonische Mittel aus Erinnerung und Präzision wird als F1-Score bezeichnet. Es bietet eine faire Messung, die sowohl falsch-positive als auch falsch-negative Ergebnisse berücksichtigt. Der F1-Score wird nach folgender Formel berechnet:
F1-Score = frac{2 imes Precision imes Recall}{Precision + Recall} Der F1-Score ist besonders nützlich, wenn Präzision und Erinnerung nicht im Gleichgewicht sind und ein Gleichgewicht zwischen beiden gewünscht wird.
