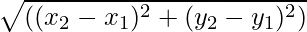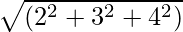logo

TechCodeview

Größe eines Vektors

Vektorgrößen sind Größen, die sowohl Richtung als auch Größe haben. Der Betrag eines Vektors ist die Länge des Vektors. Er wird durch den numerischen Wert des Vektors angegeben und ist immer positiv, da er die Länge des Vektors darstellt. Für jeden Vektor 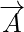overrightarrow{A}seine Größe wird dargestellt als overrightarrow{A}.

Erfahren Sie in diesem Artikel mehr über die Größe des Vektors, seine Formel, Beispiele und anderes.



Inhaltsverzeichnis

Was ist die Größe eines Vektors?

Die Größe eines Vektors wird als die Länge des Vektors definiert. Da der Betrag des Vektors die Länge des Vektors angibt, ist er immer positiv. Für jeden Vektor A wird sein Betrag als |A| dargestellt. Angenommen, ein Vektor ist als xi + yj definiert, dann ist seine Größe als Quadratwurzel der Quadratsumme der einzelnen Terme definiert. Die Größe des Vektors stellt die Länge des Vektors dar, d. h. den Wert oder die Auswirkung, die der Vektor hat.

Wenn beispielsweise eine Kraft von 5i N auf ein Objekt einwirkt, beträgt ihre Größe 5 N, was bedeutet, dass die Stärke der ausgeübten Kraft 5 N beträgt, und „ ich' in 5i stellt dar, dass es in positiver x-Richtung angewendet wird.



Größe einer Vektorformel

Es gibt verschiedene Möglichkeiten, den Betrag des Vektors zu berechnen. Verwenden Sie basierend auf den angegebenen Daten eine andere Formel, um die Größe eines Vektors zu ermitteln. Der Betrag eines Vektors A wird mit dem Modulo-Operator dargestellt, d. h. |A|

Es gibt verschiedene Formeln, mit denen die Größe des Vektors berechnet wird. Das folgende Bild zeigt die wichtigen Formeln, die zum Ermitteln der Größe des Vektors verwendet werden.

Größe einer Vektorformel

Im Folgenden finden Sie Möglichkeiten zur Berechnung der Größe.



  • Wenn ihnen ein Vektor Ā = xi+ yĵ + zk̂ gegeben wird, kann die Größe des Vektors Ā mit der folgenden Formel berechnet werden

Betrag des Vektors Ā (|A|) = √(x 2 + und 2 +z 2 )

  • Wenn der Startpunktvektor beispielsweise (x1, Und1) und der Endpunkt eines Vektors ist beispielsweise (x2, Und2) sind dann die Größe des Vektors gegeben overrightarrow{AB}ist gegeben durch,
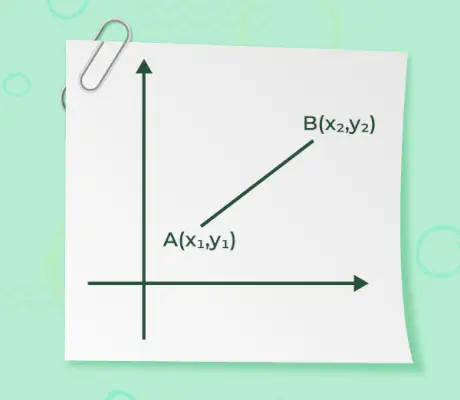
Größe des Vektors, wenn zwei Punkte angegeben sind

Die Größe eines Vektors ist, wenn der Start- und Endpunkt eines Vektors angegeben ist, nichts anderes als der Abstand zwischen den Punkten. Die Formel zum Ermitteln der Größe lautet:

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Wenn einer der Start- oder Endpunkte eines Vektors im Ursprung o(0, 0) liegt und ein anderer Punkt dort liegt A(x, y) wie in der folgenden Abbildung angegeben,
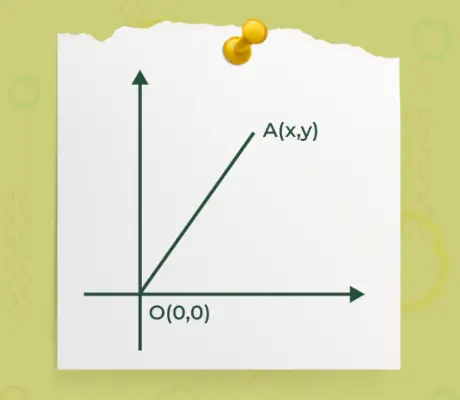
Größe des Vektors, wenn ein Punkt und ein Ursprung angegeben sind

Dann lautet die Formel zum Ermitteln der Größe eines Vektors, bei dem sich eines der Enden eines Vektors im Ursprung befindet, durch

|Ā| = √(x 2 +y 2 )

Richtung eines Vektors

Vektorgrößen sind Größen, die sowohl Betrag als auch Richtung haben. Die Richtung der Vektorgröße gibt an, in welche Richtung die Vektorgröße angewendet wird. Er ist definiert als der Winkel, den der Vektor mit der horizontalen Linie oder der x-Achse bildet. Es wird durch das Symbol dargestellt A .

Das Bild unten zeigt den Pfeil, der die Richtung des Vektors anzeigt.

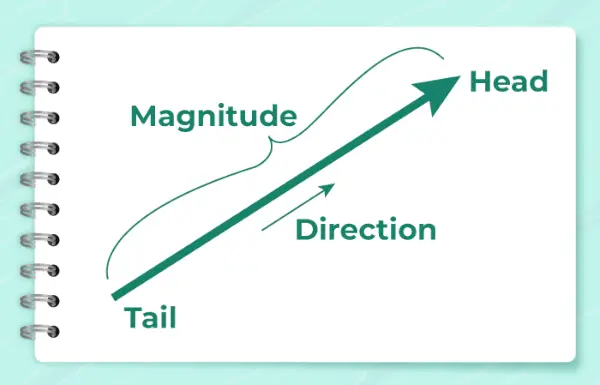
Richtung des Vektors

Es wird nach der Formel berechnet:

α = tan -1 (y/x)

So bestimmen Sie die Monitorgröße

Für den durch die Koordinaten (x1, Und1) und (x2, Und2) ihre Richtung ist durch die Formel gegeben,

α = tan -1 [(Und 2 - Und 1 )/(X 2 - X 1 )]

Wie finde ich die Größe eines Vektors?

Die Größe des Vektors wird mithilfe der unten beschriebenen Schritte berechnet:

Schritt 1: Identifizieren Sie die x-, y- und z-Komponenten des Vektors.

Schritt 2 : Ermitteln Sie das Quadrat aller x-, y- und z-Komponenten.

Schritt 3: Fügen Sie alle in Schritt 2 gefundenen Quadrate hinzu.

Sortierung nach Zufallsprinzip in SQL

Schritt 4: Finden Sie die Quadratwurzel der in Schritt 3 erhaltenen Summe.

Der nach Schritt 4 erhaltene Wert ist die Größe des angegebenen Vektors.

Beispiel: Finden Sie den Betrag des Vektors A = 3i + 4j

Lösung:

Die Größe des Vektors A wird mithilfe der oben beschriebenen Schritte berechnet.

Schritt 1: Wenn wir A = 3i + 4j mit xi + yj vergleichen, erhalten wir x = 3 und y = 4

Schritt 2: X2= 32= 9 und y2= 42= 16

Schritt 3: X2+ und2= 9 + 16 = 25

Schritt 4: √(25) = 5

Somit beträgt der Betrag des Vektors A = 3i + 4j 5 Einheiten.

Abschluss

Zusammenfassend sagt uns die Größe eines Vektors, wie lang der Vektor ist. Dieses Konzept ist in vielen Bereichen wie Physik, Ingenieurwesen und Informatik sehr wichtig, da es dabei hilft, Dinge wie Geschwindigkeit, Kraft und Bewegungsrichtung zu messen. Durch das Verständnis der Vektorgröße können wir praktische Probleme besser analysieren und lösen, was es zu einem Schlüsselwissen für jeden macht, der mit Zahlen und Messungen in realen Anwendungen arbeitet.

Mehr lesen,

Gelöste Beispiele zur Größe des Vektors

Beispiel 1: Finden Sie den Betrag für den Vektor Ā = 2i + 3ĵ + 4k.

Lösung:

Ausnahmebehandlung in Java

Gegeben,

Ā = 2i + 3ĵ + 4k

Betrag |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

Die Größe des Vektors 2i+3ĵ+4k Ist 5.38 Einheit

Beispiel 2: Finden Sie den Betrag für den Vektor Ā = 3i + 3ĵ – 6k

Lösung:

Gegeben

Ā = 3i + 3ĵ – 6k

Betrag |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

Die Größe des Vektors 3i+ 3ĵ – 6k Ist 7.35 Einheit.

Beispiel 3: Ermitteln Sie die Größe des Vektors, wenn der Startpunkt eines Vektors (3, 4) und der Endpunkt (6, 2) ist.

Lösung:

Gegeben,

(X1, Und1) = (3, 4)
(X2, Und2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

Somit beträgt die Größe des gegebenen Vektors 3.6 Einheit.

Beispiel 4: Ermitteln Sie die Größe des Vektors, wenn der Startpunkt eines Vektors (2, 1, 4) und der Endpunkt (5, 2, 6) ist.

Lösung:

Gegeben,

(X1, Und1, Mit1) = (2, 1, 4)

(X2, Und2, Mit2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Somit beträgt die Größe des gegebenen Vektors 3,74 Einheit.

Beispiel 5: Wie groß ist der Vektor, der am Ursprung und Endpunkt bei (3, 4) beginnt?

Regressionstests im Softwaretest

Lösung:

Gegeben,

Der Startpunkt des Vektors ist O(0, 0)

Endpunkt (x, y) = (3, 4)

Größe des Vektors (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Somit beträgt die Größe des gegebenen Vektors 5 Einheit.

Beispiel 6: Ermitteln Sie die Größe des Vektors, bei dem einer der Endpunkte im Ursprung und der andere Punkt bei (1, 4, 3) liegt.

Lösung:

Gegeben,

Endpunkt des Vektors ist O(0, 0)

Anderer Punkt (x, y, z) = (1, 4, 3)

Größe des Vektors (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Somit beträgt die Größe des gegebenen Vektors 5.09 Einheit.

Markdown-Bild

FAQs zur Größe eines Vektors

Was ist die Größe einer Vektorformel?

Der Betrag eines Vektors ist der numerische Wert des Vektors und definiert die Länge des Vektors. Für jeden Vektor A wird sein Betrag als |A| dargestellt. Die Größe des Vektors wird mit der Formel berechnet:

Für jeden Vektor A = xi + yj + zk ist seine Größe durch die Formel gegeben

|A| = √(x 2 + und 2 + z 2 )

Für jeden Vektor, dessen Startpunkt bzw. Endpunkt (x) ist1, Und1) und (x2, Und2) seine Größe ergibt sich aus der Formel

|A| = √((x 2 - X 1 ) 2 + (und 2 - Und 1 ) 2 )

Wie stellt man die Größe eines Vektors dar?

Die Größe des Vektors A wird durch das Symbol |A| dargestellt.

Wie finde ich die Größe eines Vektors?

Zur Berechnung der Größe des Vektors werden verschiedene Formeln verwendet. Einige davon sind:

  • |A| = √(x 2 + und 2 + z 2 ) wenn der Vektor die Form A = xi + yj + zk hat
  • |A| = √((x) 2 + (und) 2 ) wenn der Vektor durch Punkt A (x, y) und den Ursprung O(0, 0) gegeben ist.
  • |A| = √((x 2 - X 1 ) 2 + (und 2 - Und 1 ) 2 ) wenn der Vektor durch Punkt A (x1, Und2) und Punkt B (x2, Und2).

Finden Sie einen Vektor der Stärke 5.

Es gibt verschiedene Vektoren, die eine Größe von 5 haben können. Ein Beispiel dafür ist Vektor A, dargestellt als:

A = 3i + 4j Oder A = 4i + 5j