Das Newtonsche Abkühlungsgesetz ist das Grundgesetz, das die Geschwindigkeit der Wärmeübertragung eines Körpers an seine Umgebung durch Strahlung beschreibt. Dieses Gesetz besagt, dass die Rate, mit der der Körper Wärme abstrahlt, direkt proportional zum Temperaturunterschied zwischen Körper und Umgebung ist, sofern der Temperaturunterschied gering ist. Das heißt, je höher der Unterschied zwischen der Temperatur des Körpers und seiner Umgebung, desto mehr Wärme geht verloren, und je niedriger die Temperatur, desto weniger Wärme geht verloren. Das Newtonsche Abkühlungsgesetz ist ein Sonderfall des Stefan-Boltzmann-Gesetzes.

In diesem Artikel lernen wir das Newtonsche Kühlgesetz, die Newtonsche Kühlgesetzformel, ihre Ableitung, Beispiele und andere im Detail kennen.

Definition des Newtonschen Kühlgesetzes

Newton war der erste, der den Zusammenhang zwischen der Wärmeabgabe eines Körpers an seine Umgebung untersuchte. Er stellt fest, dass der Körper umso mehr Wärme abstrahlt, je größer der Temperaturunterschied zwischen dem Objekt und seiner Umgebung ist.

Newtons Gesetz der Abkühlung besagt, dass

Die Wärmeverlustrate eines Körpers ist direkt proportional zum Temperaturunterschied zwischen dem Körper und seiner Umgebung, sofern der Temperaturunterschied nicht groß ist.

Dieses Gesetz wird verwendet, um zu erklären, warum heißes Wasser oder heiße Milch, die auf einem Tisch stehen gelassen werden, schneller abkühlt als ein wenig warme Milch oder warmes Wasser, die auf dem Tisch stehen bleiben. Das Newtonsche Abkühlungsgesetz hilft uns, die Temperatur einer Person zu messen, ohne sie tatsächlich zu messen, basierend auf der Anfangstemperatur des Körpers und der Temperatur der Umgebung.

Newtons Gesetz der Kühlungsformel

Die Newtonsche Kühlformel ist eine Formel zur Berechnung der Temperatur eines Materials, wenn es durch Strahlung Wärme an seine Umgebung verliert.

Nach dem Newtonschen Abkühlungsgesetz gilt

Die Wärmeverlustrate ( – dQ/dt) des Körpers ist direkt proportional zum Temperaturunterschied [ΔT = (T ₂ - T ₁ )] des Körpers und der Umgebung.

Kat Timpf Gewicht

Wir können es darstellen als:

– dQ/dt ∝ (T ₂ - T ₁ )

– dQ/dt = k(T ₂ - T ₁ )

Wo,
k ist eine Proportionalitätskonstante

Wenn wir die obige Differentialgleichung lösen, erhalten wir:

T(t) = T _S + (T _Ö - T _S ) Es ist ^-kt

Wo,
T ist die Zeit
T(t) ist die Temperatur des Körpers zum Zeitpunkt t
T _S ist die Umgebungstemperatur
T _Ö ist die Anfangstemperatur des Körpers
k ist die Proportionalitätskonstante

Herleitung des Newtonschen Abkühlungsgesetzes

Die Formel des Newtonschen Kühlgesetzes kann mithilfe der Lösung der Differentialgleichung abgeleitet werden. Ein Körper der Masse m und der spezifischen Wärmekapazität s befinde sich bei der Temperatur T₂und T₁ist die Temperatur der Umgebung.

Wenn die Temperatur geringfügig sinkt dT ₂ rechtzeitig dt , dann beträgt die verlorene Wärmemenge

dQ = ms dT ₂

Die Wärmeverlustrate ist gegeben durch:

dQ/dt = ms (dT ₂ /dt)

Nach dem Newtonschen Abkühlungsgesetz gilt

– dQ/dt = k(T ₂ - T ₁ )

Vergleich der obigen Gleichung

– ms (dT ₂ /dt) = k (T ₂ - T ₁ )

dT ₂ /(T ₂ -T ₁ ) = – (k/ms) dt

dT ₂ /(T ₂ - T ₁ ) = – Kdt

Wo, K = k/m·s

Integrieren der obigen Gleichung

Protokoll _{Es ist} (T ₂ - T ₁ ) = – K t + c

T ₂ = T ₁ + C’ und ^–Kt

10 ml bis oz

Wo, C’ = e ^C

Der Zusammenhang zwischen dem Abfall der Körpertemperatur und der Zeit wird anhand der Abkühlungskurve dargestellt. Die Steigung dieses Diagramms zeigt die Geschwindigkeit des Temperaturabfalls.

Die Abkühlungskurve ist ein Diagramm, das den Zusammenhang zwischen Körpertemperatur und Zeit zeigt. Die Geschwindigkeit des Temperaturabfalls wird durch die Steigung der Tangente an die Kurve an jedem Punkt bestimmt. Das unten hinzugefügte Bild zeigt den Temperaturabfall und die Zeitbeziehung.

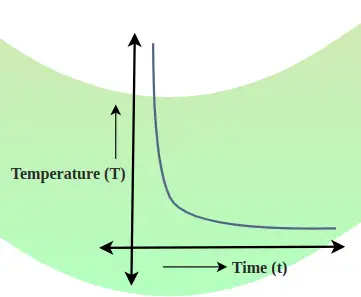
Allgemein,

T(t) = T _A +(T _H -T _A )Es ist ^-kt

Wo
T(t) ist die Temperatur zum Zeitpunkt t
T _A ist die Umgebungstemperatur oder Umgebungstemperatur
T _H ist die Temperatur des heißen Objekts
k ist die positive Konstante und t ist die Zeit

Methoden zur Anwendung des Newtonschen Abkühlungsgesetzes

Bei einer konstanten Abkühlungsrate hängt die Abkühlungsrate mit der durchschnittlichen Körpertemperatur während des Intervalls zusammen. Anschließend können wir mithilfe des Newtonschen Abkühlungsgesetzes den ungefähren Wert berechnen

dθ/dt = k(q – q _S )

Wo,
Q ist die Temperatur des Körpers
Q _S ist die Temperatur der Umgebung

Wenn nun die durchschnittliche Körpertemperatur q ist, wobei

q = (q _ich + q _F )/2

Überprüfung des Newtonschen Abkühlungsgesetzes

Wir können Newtons Abkühlungsgesetz leicht durch das unten beschriebene Experiment überprüfen:

Im Experiment nehmen wir ein doppelwandiges Gefäß (V) mit Wasser zwischen den beiden Wänden. In das doppelwandige Gefäß nehmen wir ein Kupferkalorimeter (C), das heißes Wasser enthält.

Wir verwenden zwei Thermometer T₂um die Temperaturen des Wassers im Kalorimeter und T zu messen₁um die Temperatur zu messen des Warmwassers zwischen den Doppelwänden. Nach gleichen Zeitintervallen werden beide Temperaturen notiert und zwischen den Protokollen ein Diagramm erstellt_{Es ist}(T₂-T₁) und die Zeit (t) werden aufgetragen, die als gerade Linie mit negativer Steigung erscheint.

Diagramm zum Newtonschen Kühlgesetz

Das Diagramm des Newtonschen Abkühlungsgesetzes wird unten hinzugefügt. In diesem Diagramm wird der Logarithmus der Differenz zwischen den beiden Temperaturen und der Zeit angezeigt.

Einschränkungen des Newtonschen Abkühlungsgesetzes

Verschiedene Einschränkungen des Newtonschen Abkühlungsgesetzes sind:

• Das Newtonsche Abkühlungsgesetz gilt, wenn der Temperaturunterschied zwischen Körper und Umgebung gering ist.
• Der Wärmeverlust des Körpers erfolgt lediglich in Form von Strahlung .
• Die Temperatur der Umgebung muss während der Abkühlung des Körpers konstant bleiben, andernfalls gilt das Newtonsche Abkühlungsgesetz nicht.

Anwendungen des Newtonschen Abkühlungsgesetzes

Verschiedene Anwendungen des Newtonschen Abkühlungsgesetzes sind:

• Abschätzen, wie lange es dauert, bis ein warmer Gegenstand auf eine bestimmte Temperatur abgekühlt ist.
• Zur Bestimmung der Temperatur eines Getränks im Kühlschrank nach Ablauf einer bestimmten Zeitspanne.
• Es hilft, den Zeitpunkt des Todes anzuzeigen, indem die mögliche Körpertemperatur zum Zeitpunkt des Todes und die aktuelle Körpertemperatur betrachtet werden.

Mehr lesen,

• Spezifische Wärmekapazität
• Grundkonzept der Thermodynamik
• Thermodynamische Prozesse

Gelöste Beispiele Newtons Gesetz der Abkühlung

Beispiel 1: Eine mit heißen Speisen gefüllte Pfanne kühlt bei einer Raumtemperatur von 20 °C in 2 Minuten von 94 °C auf 86 °C ab. Wie lange dauert es, von 71 °C auf 69 °C abzukühlen?

Lösung:

Der Durchschnitt von 94 °C und 86 °C beträgt 90 °C,

• T₂= 90 °C
• T₁= 20 °C

Kommen Sie vorbei. Lebensmittel erreichen in 2 Minuten eine Temperatur von 8 °C.

Nach dem Newtonschen Abkühlungsgesetz gilt

– dQ/dt = k(T ₂ -T ₁ )

8 °C /2 min = k(90 – 20)

4 = k(70) ………(1)

Der Durchschnitt von 69 °C und 71 °C beträgt 70 °C

• T₂= 70 °C
• T₁= 20 °C

Nach dem Newtonschen Abkühlungsgesetz gilt

2 °C /dt = k(70 – 20) ……(2)

Aus Gleichung (1) und (2)

Zeitänderung = 0,7 min = =42 sek

Somit dauert es 42 Sekunden, bis das Essen von 71 °C auf 69 °C abgekühlt ist.

Beispiel 2: Ein Körper mit einer Temperatur von 40 °C wird in einer Umgebung mit konstanter Temperatur von 20 °C gehalten. Es wird beobachtet, dass seine Temperatur innerhalb von 10 Minuten auf 35 °C sinkt. Finden Sie heraus, wie lange es dauert, bis der Körper eine Temperatur von 30 °C erreicht.

Lösung:

Gegeben,

• Q_ich= (40 – 20) °C
• Q_F= (35 – 20) °C

Nach dem Newtonschen Abkühlungsgesetz

Q _F = q _ich Es ist ^-kt

Nun zum Intervall, in dem die Temperatur von 40 °C auf 35 °C fällt.

(35 – 20) = (40 – 20) und^-(10k)

Es ist^-10k= 3/4

-10k = (ln 4/3)

Linux-Ausführungsbefehl

k = 0,2876/10

k = 0,02876

Verwenden Sie nun erneut die Newonsche Formel,

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

Es ist^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

Unter Verwendung des Werts von k,

t = 0,40546/0,02876

t = 14,098 min

Somit benötigt der Körper 14,098 Minuten, um die Temperatur von 30 °C zu erreichen

Beispiel 3: Das Öl wird auf 70 ºC erhitzt. Nach 6 Minuten kühlt es auf 50 °C ab. Berechnen Sie die Zeit, die das Öl benötigt, um bei gegebener Umgebungstemperatur T von 50 °C auf 40 °C abzukühlen _S = 25 °C

Lösung:

Java-Version Linux

Gegeben,

Öltemperatur nach 6 Minuten, d. h. T(t) beträgt 50 ºC

• Umgebungstemperatur T_S= 25 °C
• Temperatur des Öls, T_Ö= 70 °C
• Zeit zum Abkühlen auf 50 °C = 6 Minuten

Nach dem Newtonschen Abkühlungsgesetz gilt

T(t) = T_S+ (T₀- T_S) Es ist^-kt

{T(t) – T_S}/(T_Ö- T_S) = und^-kt

-kt = ln[(T(t) – T_S)/(T_Ö- T_S)] ………(1)

Ersetzen Sie die Werte

-kt = ln[(50 – 25)/(70 – 25)]

-k = (ln 0,55556)/6

k = 0,09796

Die Durchschnittstemperatur von 50 ºC bis 40 ºC beträgt 45 ºC

Wiederum unter Verwendung des Newtonschen Abkühlungsgesetzes

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

-0,09796t = ln(0,44444)

0,09796 t = 0,81093

t = 0,09796/0,58778 = 8,278 Min

Somit beträgt die Zeit, die das Öl benötigt, um von 50 °C auf 40 °C abzukühlen 8,278 Min

Beispiel 4: Wasser wird 10 Minuten lang auf 80 °C erhitzt. Wie hoch wäre seine Temperatur in Grad Celsius, wenn k = 0,056 pro Minute und die Umgebungstemperatur 25 ºC beträgt?

Lösung:

Gegeben,

• Umgebungstemperatur T_S= 25 °C
• Temperatur des Wassers T₀= 80 °C
• Zeit, für die Wasser erhitzt wird (t) = 10 min
• Wert der Konstante k = 0,056.

Nach dem Newtonschen Abkühlungsgesetz gilt

T(t) = T_S+ (T₀- T_S) Es ist^-kt

Den Wert ersetzen

T(t)= 25 + (80 – 25)e^-(0,056×10)

T(t) = 25 + 55 e^-(0,056×10)

T(t) = 25 + 31,42

T(t) = 56,42

Nach 10 Minuten wäre die Wassertemperatur erreicht 56,42 °C.

Bash verkettet Zeichenfolgen

FAQs zum Newtonschen Kühlgesetz

F1: Was ist Newtons Abkühlungsgesetz?

Antwort:

Das Newtonsche Abkühlungsgesetz besagt, dass die Wärmeverlustrate eines Körpers direkt proportional zum Temperaturunterschied zwischen dem Körper und seiner Umgebung ist.

F2: Wie lautet die Formel des Newtonschen Kühlgesetzes?

Antwort:

Die Formel des Newtonschen Kühlgesetzes besagt:

T(t) = T _S + (T _Ö - T _S ) Es ist ^-kt

F3: Was ist k im Newtonschen Abkühlungsgesetz?

Antwort:

Der k Im Newtonschen Kühlgesetz ist die Formel die Konstante, die vom Material abhängt, d. h. eine Änderung des Materials ändert die k im Newtonschen Gesetz der Abkühlung.

F4: Warum lässt sich heiße Milch leichter aus einer Schüssel trinken als aus einem Glas?

Antwort:

Eine Schüssel hat eine größere Oberfläche als Glas, daher geht mehr Wärme in Form von Wärmestrahlung durch die Schüssel an die Umgebung verloren und es ist für uns daher einfacher, heiße Milch aus der Schüssel zu trinken.