- Pushdown-Automaten sind eine Möglichkeit, ein CFG auf die gleiche Weise zu implementieren, wie wir DFA für eine reguläre Grammatik entwerfen. Ein DFA kann sich eine begrenzte Menge an Informationen merken, ein PDA kann sich jedoch eine unendliche Menge an Informationen merken.
- Pushdown-Automaten sind einfach ein NFA, der um einen „externen Stapelspeicher“ erweitert wird. Das Hinzufügen eines Stapels wird verwendet, um Pushdown-Automaten eine Last-In-First-Out-Speicherverwaltungsfunktion bereitzustellen. Pushdown-Automaten können eine unbegrenzte Menge an Informationen auf dem Stapel speichern. Es kann auf eine begrenzte Menge an Informationen im Stapel zugreifen. Ein PDA kann ein Element auf die Oberseite des Stapels schieben und ein Element von der Oberseite des Stapels abheben. Um ein Element in den Stapel einzulesen, müssen die obersten Elemente abgenommen werden und gehen verloren.
- Ein PDA ist leistungsfähiger als FA. Jede Sprache, die von FA akzeptiert werden kann, kann auch von PDA akzeptiert werden. PDA akzeptiert auch eine Sprachklasse, die nicht einmal von FA akzeptiert werden kann. Somit ist PDA FA deutlich überlegen.
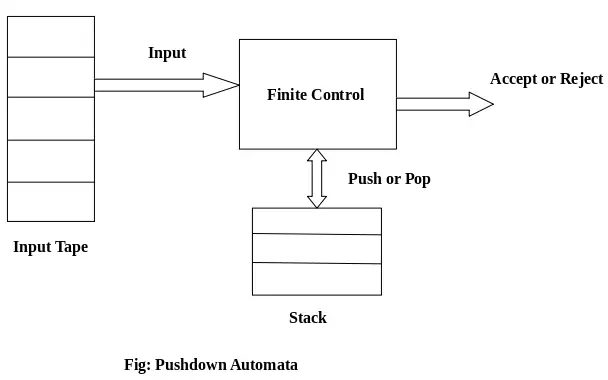
PDA-Komponenten:
Eingabeband: Das Eingabeband ist in viele Zellen oder Symbole unterteilt. Der Eingabekopf ist schreibgeschützt und kann sich jeweils nur um ein Symbol von links nach rechts bewegen.
Endliche Kontrolle: Das endliche Steuerelement verfügt über einen Zeiger, der auf das aktuelle Symbol zeigt, das gelesen werden soll.
Stapel: Der Stapel ist eine Struktur, in der wir die Gegenstände nur an einem Ende schieben und entfernen können. Es hat eine unendliche Größe. Beim PDA dient der Stapel zur Zwischenspeicherung der Gegenstände.
Formale Definition von PDA:
Der PDA kann als eine Sammlung von 7 Komponenten definiert werden:
Q: die endliche Menge von Zuständen
∑: der Eingabesatz
C: ein Stapelsymbol, das vom Stapel geschoben und entnommen werden kann
q0: der Ausgangszustand
Periodenschlüssel
MIT: ein Startsymbol, das in Γ liegt.
F: eine Reihe von Endzuständen
D: Zuordnungsfunktion, die zum Übergang vom aktuellen Status zum nächsten Status verwendet wird.
Momentane Beschreibung (ID)
ID ist eine informelle Notation dafür, wie ein PDA eine Eingabezeichenfolge berechnet und entscheidet, ob die Zeichenfolge akzeptiert oder abgelehnt wird.
Eine momentane Beschreibung ist ein Tripel (q, w, α), wobei:
Q beschreibt den aktuellen Zustand.
In beschreibt die verbleibende Eingabe.
Säureeigenschaften in DBMS
A beschreibt den Stapelinhalt, oben links.
Drehkreuz-Notation:
Das ⊢-Zeichen beschreibt die Drehkreuz-Notation und stellt eine Bewegung dar.
Das ⊢*-Zeichen beschreibt eine Folge von Zügen.
Zum Beispiel,
(p, b, T) ⊢ (q, w, α)
Beispiele für Python-Programme
Im obigen Beispiel wird beim Übergang vom Zustand p zum Zustand q das Eingabesymbol „b“ verbraucht und der obere Teil des Stapels „T“ wird durch eine neue Zeichenfolge α dargestellt.
Beispiel 1:
Entwerfen Sie einen PDA zum Akzeptieren einer Sprache aNB2n.
Lösung: In dieser Sprache sollten auf n a-Zeichen 2n b-Zeichen folgen. Daher wenden wir eine sehr einfache Logik an: Wenn wir ein einzelnes „a“ lesen, legen wir zwei a auf den Stapel. Sobald wir „b“ lesen, sollte für jedes einzelne „b“ nur ein „a“ vom Stapel entfernt werden.
Die ID kann wie folgt aufgebaut sein:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa)
Wenn wir nun b lesen, ändern wir den Status von q0 auf q1 und beginnen mit dem Popup des entsprechenden „a“. Somit,
δ(q0, b, a) = (q1, ε)
Daher wird dieser Vorgang des Platzierens von „b“ wiederholt, es sei denn, alle Symbole werden gelesen. Beachten Sie, dass der Knallvorgang nur im Zustand q1 erfolgt.
δ(q1, b, a) = (q1, ε)
Nachdem alle b's gelesen wurden, sollten alle entsprechenden a's gelöscht werden. Wenn wir also ε als Eingabesymbol lesen, sollte sich nichts im Stapel befinden. Daher wird der Umzug sein:
δ(q1, ε, Z) = (q2, ε)
Wo
PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})
Wir können die ID wie folgt zusammenfassen:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε)
Jetzt simulieren wir diesen PDA für die Eingabezeichenfolge „aaabbbbbbb“.
δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT
Beispiel 2:
Entwerfen Sie einen PDA zur Annahme einer Sprache 0N1M0N.
Lösung: In diesem PDA folgt auf n Nullen eine beliebige Anzahl von Einsen, gefolgt von n Nullen. Daher lautet die Logik für das Design eines solchen PDA wie folgt:
Schieben Sie alle Nullen auf den Stapel, wenn Sie auf die ersten Nullen stoßen. Wenn wir dann 1 lesen, tun Sie einfach nichts. Dann lesen Sie 0 und nehmen Sie bei jedem Lesevorgang von 0 eine 0 vom Stapel.
String-Split-Bash
Zum Beispiel:

Dieses Szenario kann in der ID-Form wie folgt geschrieben werden:
δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state)
Jetzt simulieren wir diesen PDA für die Eingabezeichenfolge „0011100“.
δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT
