Schnelle Sorte ist ein interner Algorithmus, der auf der Divide-and-Conquer-Strategie basiert. In diesem:
- Die Anordnung der Elemente wird wiederholt in Teile geteilt, bis eine weitere Aufteilung nicht mehr möglich ist.
- Es ist auch bekannt als Partitionsaustauschsortierung .
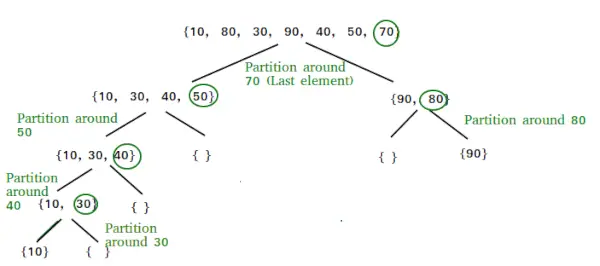
- Es verwendet ein Schlüsselelement (Pivot) zur Partitionierung der Elemente.
- Eine linke Partition enthält alle Elemente, die kleiner als das Pivotelement sind, und eine rechte Partition enthält alle Elemente, die größer als das Schlüsselelement sind.
 Zusammenführen, sortieren ist ein externer Algorithmus und basiert auf der Divide-and-Conquer-Strategie. In diesem:
Zusammenführen, sortieren ist ein externer Algorithmus und basiert auf der Divide-and-Conquer-Strategie. In diesem:
- Die Elemente werden immer wieder in zwei Unterarrays (n/2) aufgeteilt, bis nur noch ein Element übrig bleibt.
- Die Zusammenführungssortierung verwendet zusätzlichen Speicher zum Sortieren des Hilfsarrays.
- Die Zusammenführungssortierung verwendet drei Arrays, von denen zwei zum Speichern jeder Hälfte verwendet werden und das dritte externe Array zum Speichern der endgültigen sortierten Liste durch Zusammenführen der beiden anderen verwendet wird und jedes Array dann rekursiv sortiert wird.
- Zuletzt werden alle Unterarrays zusammengeführt, um die Größe des Arrays auf „n“ zu erhöhen.

Schnelle Sortierung vs. Zusammenführungssortierung
- Aufteilung der Elemente im Array: Bei der Zusammenführungssortierung wird das Array in nur zwei Hälften geteilt (d. h. n/2). wohingegen bei einer schnellen Sortierung das Array in ein beliebiges Verhältnis aufgeteilt wird. Es besteht kein Zwang, das Array von Elementen bei der Schnellsortierung in gleiche Teile zu unterteilen. Worst-Case-Komplexität: Die Worst-Case-Komplexität der schnellen Sortierung ist O(n^2), da im schlechtesten Zustand viele Vergleiche erforderlich sind. wohingegen bei der Zusammenführungssortierung der schlechteste und der durchschnittliche Fall die gleiche Komplexität O(n log n) haben. Verwendung mit Datensätzen: Die Zusammenführungssortierung kann bei jeder Art von Datensätzen unabhängig von ihrer Größe (groß oder klein) gut funktionieren. wohingegen die Schnellsortierung bei großen Datenmengen nicht gut funktionieren kann. Zusätzlicher Speicherplatzbedarf: Die Zusammenführungssortierung ist nicht vorhanden, da sie zusätzlichen Speicherplatz zum Speichern der Hilfsarrays erfordert. wohingegen die Schnellsortierung vorhanden ist, da sie keinen zusätzlichen Speicher erfordert. Effizienz: Die Zusammenführungssortierung ist effizienter und funktioniert bei größeren Arrays oder Datensätzen schneller als die Schnellsortierung. wohingegen die Schnellsortierung effizienter ist und bei kleineren Array-Größen oder Datensätzen schneller arbeitet als die Zusammenführungssortierung. Sortiermethode: Die Schnellsortierung ist eine interne Sortiermethode, bei der die Daten im Hauptspeicher sortiert werden. wohingegen die Zusammenführungssortierung eine externe Sortiermethode ist, bei der die zu sortierenden Daten nicht im Speicher untergebracht werden können und für die Sortierung Hilfsspeicher benötigt werden. Stabilität: Die Zusammenführungssortierung ist stabil, da zwei Elemente mit gleichem Wert in der sortierten Ausgabe in derselben Reihenfolge erscheinen wie im unsortierten Eingabearray. wohingegen die schnelle Sortierung in diesem Szenario instabil ist. Aber es kann durch einige Änderungen im Code stabilisiert werden. Bevorzugt für: Die schnelle Sortierung wird für Arrays bevorzugt. wohingegen die Zusammenführungssortierung für verknüpfte Listen bevorzugt wird. Referenzlokalität: Quicksort weist eine gute Cache-Lokalität auf und macht Quicksort daher schneller als Merge-Sortierung (in vielen Fällen wie in einer virtuellen Speicherumgebung).
| Vergleichsbasis | Schnelle Sorte | Zusammenführen, sortieren |
|---|---|---|
| Die Partition der Elemente im Array | Die Aufteilung eines Arrays von Elementen erfolgt in einem beliebigen Verhältnis, nicht unbedingt in zwei Hälften. | Bei der Zusammenführungssortierung wird das Array in nur zwei Hälften geteilt (d. h. n/2). |
| Worst-Case-Komplexität | O(n^2) | O(nlogn) |
| Funktioniert gut | Es funktioniert gut auf kleineren Arrays | Es funktioniert einwandfrei auf Arrays jeder Größe |
| Geschwindigkeit der Ausführung | Es arbeitet schneller als andere Sortieralgorithmen für kleine Datensätze wie die Auswahlsortierung usw | Die Geschwindigkeit ist bei jeder Datengröße konstant |
| Zusätzlicher Speicherplatzbedarf | Weniger (vor Ort) | Mehr (nicht vor Ort) |
| Effizienz | Ineffizient für größere Arrays | Effizienter |
| Sortiermethode | Intern | Extern |
| Stabilität | Nicht stabil | Stabil |
| Bevorzugt für | für Arrays | für verknüpfte Listen |
| Bezugsort | Gut | arm |
| Hauptarbeit | Die Hauptarbeit besteht darin, das Array in zwei Unterarrays zu unterteilen, bevor sie rekursiv sortiert werden. | Die Hauptarbeit besteht darin, die beiden Unterarrays zu kombinieren, nachdem sie rekursiv sortiert wurden. |
| Aufteilung des Arrays | Die Aufteilung eines Arrays in Unterarrays kann ausgeglichen sein oder auch nicht, da das Array um den Drehpunkt herum aufgeteilt ist. | Die Aufteilung eines Arrays in Unterarrays ist immer ausgeglichen, da das Array genau in der Mitte geteilt wird. |
| Methode | Bei der Schnellsortierung handelt es sich um eine Sortiermethode direkt vor Ort. | Die Zusammenführungssortierung ist keine ortsgebundene Sortiermethode. |
| Zusammenführen | Quicksort erfordert keine explizite Zusammenführung der sortierten Unterarrays; Vielmehr wurden die Unterarrays während der Partitionierung ordnungsgemäß neu angeordnet. | Die Zusammenführungssortierung führt eine explizite Zusammenführung sortierter Unterarrays durch. |
| Raum | Quicksort benötigt keinen zusätzlichen Array-Speicherplatz. | Zum Zusammenführen sortierter Unterarrays ist ein temporäres Array erforderlich, dessen Größe der Anzahl der Eingabeelemente entspricht. |
