Ein Kreis besteht aus Punkten, die alle den gleichen Abstand vom Kreismittelpunkt haben. Eine geschlossene geometrische Form ist ein Kreis. Im Alltag sehen wir Kreise in Form eines Rades, Pizzen, einen runden Boden und so weiter.

Teile eines Kreises

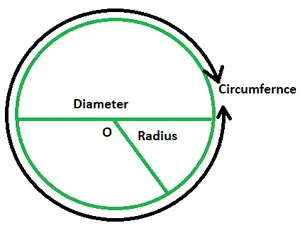
Schlüsselbegriffe:

• Radius: Der Radius eines Kreises ist der Abstand zwischen seinem Mittelpunkt und einem beliebigen Punkt am Rand. Es wird allgemein als r bezeichnet. Ein Kreis hat unendlich viele Radien.
• Durchmesser: Es ist eine Linie, die durch die Mitte verläuft und deren Enden auf dem Kreis liegen. Er wird mit D bezeichnet und ist doppelt so groß wie der Kreisradius.
• Umfang: Die Ausdehnung des Kreisrandes entspricht seinem Umfang. Dies bedeutet, dass der Umfang eines Kreises seinem Umfang entspricht. Der Umfang des Kreises entspricht der Länge des Fadens, der sauber um seinen Umfang gewickelt ist. Sie wird mit 2πr angegeben.

Was ist die Kreisfläche?

Die Fläche eines Kreises bezieht sich auf die Menge an Raum, die von der Kante eines Kreises umschlossen wird. Die vom Kreis ausgefüllte Fläche ist das Gebiet innerhalb des Kreisumfangs. Sie wird auch als Gesamtzahl der im Kreis enthaltenen Quadrateinheiten bezeichnet.

Überprüfen: Durchmesser eines Kreises

Blasensortierung im Algorithmus

Kreisflächenformeln

Die Oberfläche eines Kreises ergibt sich aus der folgenden Formel:

A = πr ²

wobei r der Radius des gegebenen Kreises ist.

oder

A = C ² /4p

wobei C der Umfang des gegebenen Kreises ist.

Beispiele für die Verwendung der Kreisflächenformel

Frage 1: Ermitteln Sie die Fläche eines Kreises mit einem Radius von 8 m.

Lösung:

Gegeben: r = 8 m

Da die Fläche eines Kreises = πr ist²

A = π(8)²

= 64p

= 200,96 m ²

Frage 2: Ermitteln Sie die Fläche eines Kreises mit einem Umfang von 12 cm.

Lösung:

Gegeben: C = 12 cm

Da A = C²/4p

= 12²/4p

= 11,46 cm ²

Frage 3. Ermitteln Sie die Fläche eines Kreises mit einem Durchmesser von 12 cm.

Lösung:

Gegeben: D = 12 cm

oder Radius = r = 12/2 = 6 cm

Da A = πr²

= π(6)2

= 113,04 cm ²

Frage 4: Ermitteln Sie die Fläche eines Kreises mit einem Radius von 9 cm.

Lösung:

Gegeben: r = 9 m

Da die Fläche eines Kreises = πr ist²

A = π(9)²

= 81p

= 254,34 cm ²

Frage 5. Ermitteln Sie die Fläche eines Kreises mit einem Durchmesser von 10 cm.

Lösung:

Gegeben: D = 10 cm

oder Radius = r = 10/2 = 5 cm

Da A = πr²

= π(5)²

= 78,5 cm ²

Überprüfen Sie auch:

• Fläche eines Kreisrechners
• Quadratmeterzahl des Kreisrechners
• Radius eines Kreisrechners
• Durchmesser eines Kreisrechners
• Umfangsrechner
• Umfang-zu-Durchmesser-Rechner