In diesem Artikel werden wir die Baumdurchquerung in der Datenstruktur diskutieren. Der Begriff „Baumdurchquerung“ bedeutet das Durchqueren oder Besuchen jedes Knotens eines Baums. Es gibt eine einzige Möglichkeit, die lineare Datenstruktur wie verknüpfte Liste, Warteschlange und Stapel zu durchlaufen. Es gibt hingegen mehrere Möglichkeiten, einen Baum zu durchlaufen, die wie folgt aufgeführt sind:
- Durchquerung vorbestellen
- Inorder-Durchquerung
- Durchquerung von Postanweisungen
In diesem Artikel werden wir die oben aufgeführten Techniken zum Durchqueren eines Baums diskutieren. Beginnen wir nun mit der Diskussion der Arten der Baumdurchquerung.
Durchquerung vorbestellen
Diese Technik folgt der Richtlinie „Wurzel links rechts“. Dies bedeutet, dass der erste Wurzelknoten besucht wird, danach der linke Teilbaum rekursiv durchlaufen wird und schließlich der rechte Teilbaum rekursiv durchlaufen wird. Da der Wurzelknoten vor (oder vor) dem linken und rechten Teilbaum durchlaufen wird, spricht man von einer Vorbestellungsdurchquerung.
Bei einem Preorder-Traversal wird also jeder Knoten vor seinen beiden Teilbäumen besucht.
Zu den Anwendungen der Vorbestellungsdurchquerung gehören:
- Es wird verwendet, um eine Kopie des Baums zu erstellen.
- Es kann auch verwendet werden, um den Präfixausdruck eines Ausdrucksbaums abzurufen.
Algorithmus
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Beispiel
Sehen wir uns nun das Beispiel der Preorder-Traversal-Technik an.
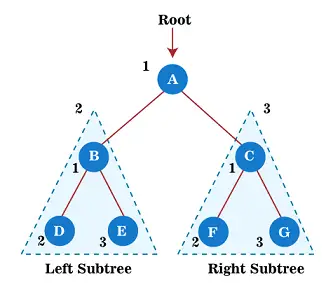
Beginnen Sie nun mit der Anwendung der Vorbestellungsdurchquerung auf den obigen Baum. Zuerst durchlaufen wir den Wurzelknoten A; Gehen Sie danach zum linken Teilbaum B , das auch in der Vorbestellung durchlaufen wird.
Für den linken Teilbaum B also zunächst den Wurzelknoten B wird selbst durchquert; danach der linke Teilbaum D wird durchquert. Seit Knoten D hat keine Kinder, in den rechten Teilbaum verschieben UND . Da Knoten E ebenfalls keine Kinder hat, ist die Durchquerung des linken Teilbaums von Wurzelknoten A abgeschlossen.
meine Monitorgröße
Gehen Sie nun zum rechten Teilbaum des Wurzelknotens A, der C ist. Für den rechten Teilbaum C also zuerst den Wurzelknoten C hat sich selbst durchquert; danach der linke Teilbaum F wird durchquert. Seit Knoten F keine Kinder hat, wechseln Sie in den rechten Unterbaum G . Da Knoten G ebenfalls keine Kinder hat, ist die Durchquerung des rechten Teilbaums von Wurzelknoten A abgeschlossen.
Daher werden alle Knoten des Baums durchlaufen. Die Ausgabe der Vorbestellungsdurchquerung des obigen Baums lautet also:
A → B → D → E → C → F → G
Um mehr über die Vorbestellungsdurchquerung in der Datenstruktur zu erfahren, können Sie dem Link folgen Durchquerung vorbestellen .
Durchquerung von Postanweisungen
Diese Technik folgt der „Links-Rechts-Wurzel“-Politik. Dies bedeutet, dass der erste linke Teilbaum des Wurzelknotens durchlaufen wird, danach der rechte Teilbaum rekursiv durchlaufen wird und schließlich der Wurzelknoten durchlaufen wird. Da der Wurzelknoten nach dem linken und rechten Teilbaum durchlaufen wird, spricht man von Postorder-Traversal.
Bei einem Postorder-Traversal wird also jeder Knoten nach seinen beiden Teilbäumen besucht.
Zu den Anwendungen der Postorder-Traversierung gehören:
- Es wird verwendet, um den Baum zu löschen.
- Es kann auch verwendet werden, um den Postfix-Ausdruck eines Ausdrucksbaums abzurufen.
Algorithmus
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Beispiel
Schauen wir uns nun das Beispiel der Postorder-Traversal-Technik an.
Wie groß ist mein Monitor?

Beginnen Sie nun mit der Anwendung der Postorder-Traversierung auf den obigen Baum. Zuerst durchlaufen wir den linken Teilbaum B, der in der Nachfolge durchlaufen wird. Danach werden wir den rechten Teilbaum durchlaufen C im Postorder. Und schließlich der Wurzelknoten des obigen Baums, d. h. A , wird durchlaufen.
Also für den linken Teilbaum B zunächst seinen linken Teilbaum D wird durchquert. Seit Knoten D Hat keine Kinder, durchqueren Sie den rechten Teilbaum UND . Da Knoten E ebenfalls keine Kinder hat, wechseln Sie zum Wurzelknoten B. Nach dem Durchqueren des Knotens B, Die Durchquerung des linken Teilbaums von Wurzelknoten A ist abgeschlossen.
Bewegen Sie sich nun zum rechten Teilbaum des Wurzelknotens A, der C ist. Für den rechten Teilbaum C also zuerst seinen linken Teilbaum F wird durchquert. Seit Knoten F Hat keine Kinder, durchqueren Sie den rechten Teilbaum G . Da der Knoten G auch keine Kinder hat, ist schließlich der Wurzelknoten des rechten Teilbaums, d. h. C, wird durchquert. Die Durchquerung des rechten Teilbaums des Wurzelknotens A ist abgeschlossen.
Durchqueren Sie schließlich den Wurzelknoten eines bestimmten Baums, d. h. A . Nach dem Durchlaufen des Wurzelknotens ist die Postorder-Durchquerung des angegebenen Baums abgeschlossen.
Daher werden alle Knoten des Baums durchlaufen. Die Ausgabe der Postorder-Durchquerung des obigen Baums lautet also:
D → E → B → F → G → C → A
Um mehr über das Postorder-Traversal in der Datenstruktur zu erfahren, können Sie dem Link folgen Durchquerung von Postanweisungen .
Inorder-Durchquerung
Diese Technik folgt der „Links-Wurzel-Rechts“-Politik. Dies bedeutet, dass der erste linke Teilbaum besucht wird, nachdem dieser Wurzelknoten durchquert wurde, und schließlich der rechte Teilbaum durchquert wird. Da der Wurzelknoten zwischen dem linken und dem rechten Teilbaum durchlaufen wird, wird dies als Inorder-Traversal bezeichnet.
Beim Inorder-Traversal wird also jeder Knoten zwischen seinen Teilbäumen besucht.
Git, füge alles hinzu
Zu den Anwendungen der Inorder-Traversierung gehören:
- Es wird verwendet, um die BST-Knoten in aufsteigender Reihenfolge abzurufen.
- Es kann auch verwendet werden, um den Präfixausdruck eines Ausdrucksbaums abzurufen.
Algorithmus
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Beispiel
Schauen wir uns nun das Beispiel der Inorder-Traversal-Technik an.

Beginnen Sie nun mit der Anwendung der Inorder-Traversierung auf den obigen Baum. Zuerst durchlaufen wir den linken Teilbaum B das wird in der Reihenfolge durchlaufen. Danach werden wir den Wurzelknoten durchlaufen A . Und schließlich der richtige Teilbaum C wird in der Reihenfolge durchlaufen.
Also für den linken Teilbaum B Zunächst der linke Teilbaum D wird durchquert. Seit Knoten D hat keine Kinder, also nach dem Durchlaufen Knoten B Es wird durchlaufen, und schließlich wird der rechte Teilbaum von Knoten B durchlaufen UND , wird durchlaufen. Knoten E hat auch keine Kinder; Daher ist die Durchquerung des linken Teilbaums des Wurzelknotens A abgeschlossen.
Durchlaufen Sie anschließend den Wurzelknoten eines bestimmten Baums, d. h. A .
Bewegen Sie sich schließlich zum rechten Teilbaum des Wurzelknotens A, der C ist. Also für den rechten Teilbaum C; Zuerst der linke Teilbaum F wird durchquert. Seit Knoten F hat keine Kinder, Knoten C wird durchlaufen und schließlich ein rechter Teilbaum von Knoten C, d. h. G , wird durchlaufen. Knoten G hat auch keine Kinder; Daher ist die Durchquerung des rechten Teilbaums des Wurzelknotens A abgeschlossen.
Wenn alle Knoten des Baums durchlaufen werden, ist die Inorder-Traversierung des gegebenen Baums abgeschlossen. Die Ausgabe der Inorder-Durchquerung des obigen Baums ist -
Python rstrip
D → B → E → A → F → C → G
Um mehr über das Inorder-Traversal in der Datenstruktur zu erfahren, können Sie dem Link folgen Inorder-Durchquerung .
Komplexität von Tree-Traversal-Techniken
Die zeitliche Komplexität der oben diskutierten Baumdurchquerungstechniken beträgt An) , Wo 'N' ist die Größe des Binärbaums.
Die räumliche Komplexität der oben diskutierten Baumdurchquerungstechniken hingegen ist O(1) wenn wir die Stapelgröße für Funktionsaufrufe nicht berücksichtigen. Ansonsten ist die räumliche Komplexität dieser Techniken groß Oh) , Wo 'H' ist die Höhe des Baumes.
Implementierung der Baumdurchquerung
Sehen wir uns nun die Implementierung der oben besprochenen Techniken unter Verwendung verschiedener Programmiersprachen an.
Programm: Schreiben Sie ein Programm zur Implementierung von Baumdurchlauftechniken in C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Ausgabe

Programm: Schreiben Sie ein Programm zur Implementierung von Baumdurchlauftechniken in C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Ausgabe
Java-flüchtiges Schlüsselwort

Programm: Schreiben Sie ein Programm zur Implementierung von Baumdurchlauftechniken in C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Ausgabe
Nach der Ausführung des obigen Codes lautet die Ausgabe:

Abschluss
In diesem Artikel haben wir die verschiedenen Arten von Baum-Traversal-Techniken besprochen: Preorder-Traversal, Inorder-Traversal und Postorder-Traversal. Wir haben diese Techniken zusammen mit Algorithmen, Beispielen, Komplexität und Implementierung in C, C++, C# und Java gesehen.
Das ist also alles über den Artikel. Ich hoffe, es wird für Sie hilfreich und informativ sein.
