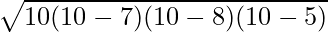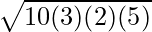Ein spitzwinkliges Dreieck ist ein Dreieck, bei dem alle Winkel der Dreiecke spitze Winkel sind. Aufgrund der Winkelsummeneigenschaft des Dreiecks kann ein Dreieck nur einen Winkel haben, entweder einen rechten oder einen stumpfen Winkel. Und daher wird das Dreieck, bei dem alle drei Winkel spitze Winkel sind, d. h. Winkel mit einem Wert von weniger als 90 Grad, ein spitzwinkliges Dreieck genannt.
Basierend auf den Arten der Innenwinkel des Dreiecks kann ein Dreieck in drei Kategorien eingeteilt werden: spitzwinklige Dreiecke, stumpfwinklige Dreiecke und rechtwinklige Dreiecke. Lassen Sie uns nun in diesem Artikel mehr über spitzwinklige Dreiecke, ihre Typen, Eigenschaften und andere Einzelheiten im Detail erfahren.
Rekha-Alter
Was ist ein spitzwinkliges Dreieck?
Ein spitzwinkliges Dreieck ist definiert als ein Dreieck, dessen drei Innenwinkel alle spitz sind, d. h. ihr Wert liegt zwischen 0° und 90°. Abhängig von der Art des Dreiecks können die Seitenlängen eines spitzwinkligen Dreiecks gleich oder ungleich sein. Auch ein spitzwinkliges Dreieck folgt der Winkelsummeneigenschaft des Dreiecks.
Die folgende Abbildung zeigt ein spitzwinkliges Dreieck mit den Innenwinkeln 45°, 35° und 80°. Da die drei Innenwinkel kleiner als 90° sind, handelt es sich bei dem gegebenen Dreieck um ein spitzwinkliges Dreieck.
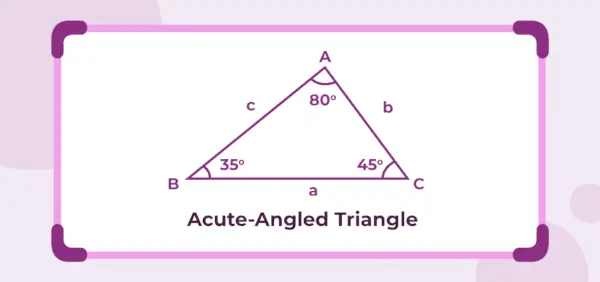
Definition des spitzwinkligen Dreiecks
Spitzwinklige Dreiecke werden, wie der Name schon sagt, als Dreiecke definiert, bei denen alle drei Winkel des Dreiecks spitze Winkel sind. Die Seiten in spitzwinkligen Dreiecken können gleich oder ungleich sein und werden auf dieser Grundlage weiter in drei Teile unterteilt, die im folgenden Artikel besprochen werden:
Arten von spitzwinkligen Dreiecken
Spitzwinklige Dreiecke werden abhängig von der Seitenlänge der Dreiecke in drei Typen eingeteilt:
- Gleichseitiges spitzes Dreieck
- Gleichschenkliges spitzes Dreieck
- Akutes Skalenusdreieck
Lassen Sie uns nun mehr über sie im Detail erfahren.
Gleichseitiges spitzes Dreieck
Ein gleichseitiges spitzes Dreieck, auch gleichseitiges Dreieck genannt, ist ein Dreieck, in dem alle Winkel spitze Winkel sind und alle Winkel gleich sind und auch die Seiten der gleichseitigen spitzen Dreiecke gleich sind. Jeder Winkel eines gleichseitigen spitzen Dreiecks beträgt immer 60°.
Gleichschenkliges spitzes Dreieck
Ein gleichschenkliges spitzes Dreieck ist ein Dreieck, in dem alle Winkel spitze Winkel sind und zwei beliebige Winkel des Dreiecks und die diesen Winkeln entsprechende Seite gleich sind. Das heißt, im gleichschenkligen spitzen Dreieck haben wir zwei Seiten und ihre entsprechenden Winkel sind gleich.
Akutes Skalenusdreieck
Ein ungleichseitiges spitzes Dreieck ist ein Dreieck, in dem alle Winkel spitze Winkel sind und keine zwei Winkel und keine zwei Seiten gleich sind. Das heißt, im ungleichseitigen spitzen Dreieck gibt es keine gleichen Seiten und keine gleichen Winkel.
Eigenschaften des spitzwinkligen Dreiecks
Im Folgenden sind einige wichtige Eigenschaften eines spitzwinkligen Dreiecks aufgeführt:
- Innenwinkel des spitzwinkligen Dreiecks sind spitze Winkel, d. h. die Winkel sind größer als 0°, aber kleiner als 90°.
- Innenwinkel der spitzwinkligen Dreiecke folgen der Winkelsummeneigenschaft, d. h. die Summe der Winkel des spitzwinkligen Dreiecks beträgt 180°.
- Ein gleichseitiges Dreieck ist immer ein spitzwinkliges Dreieck, da jeder Innenwinkel eines gleichseitigen Dreiecks 60° beträgt.
- Ein Dreieck kann nicht gleichzeitig ein rechtwinkliges Dreieck und ein spitzwinkliges Dreieck sein.
- Ein Dreieck kann nicht gleichzeitig ein spitzwinkliges Dreieck und ein stumpfwinkliges Dreieck sein.
- Im spitzwinkligen Dreieck ist die dem kleinsten Winkel gegenüberliegende Seite die kleinste und das Gegenteil gilt auch.
- Ebenso ist die dem größten Winkel gegenüberliegende Seite die größte, und das Gegenteil gilt auch.
Formeln für spitzwinklige Dreiecke
Fläche und Umfang sind die beiden Grundformeln eines spitzwinkligen Dreiecks, die im Folgenden erläutert werden.
Umfang eines spitzwinkligen Dreiecks
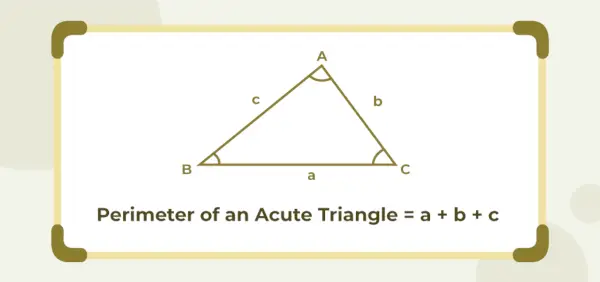
Der Umfang eines spitzwinkligen Dreiecks ist gleich der Summe seiner drei Seitenlängen. Wenn a, b und c die Seitenlängen eines spitzwinkligen Dreiecks sind, dann wird sein Umfang als (a + b + c)-Einheiten angegeben.
Umfang des spitzwinkligen Dreiecks = (a + b + c) Einheiten
Wo A , B , Und C sind die Seitenlängen des Dreiecks.
Mehr lesen, Umfang eines Dreiecks
Fläche des spitzwinkligen Dreiecks
Die Fläche eines Dreiecks ist definiert als der Gesamtraum, der von den drei Seiten eines beliebigen Dreiecks in einer zweidimensionalen Ebene umschlossen wird.
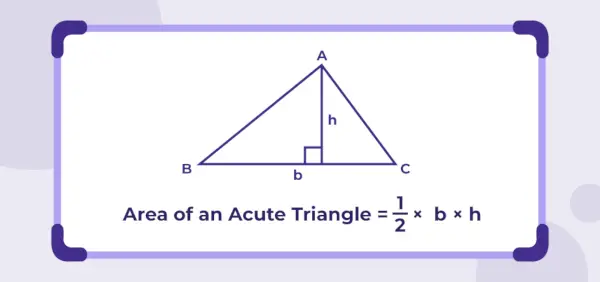
Fläche des spitzwinkligen Dreiecks = ½ × b × h
Wo,
b ist die Basislänge und h ist die Höhe des Dreiecks.
Mehr lesen, Fläche eines Dreiecks
Akuter Dreiecksbereich nach Heron’s Formula
Wenn die drei Seitenlängen eines spitzwinkligen Dreiecks angegeben sind, kann seine Fläche mit der Heron-Formel berechnet werden.
Fläche des spitzwinkligen Dreiecks =
Wo,
s ist der Halbumfang und s = (a + b + c)/2 , Du , B , Und C sind die Seitenlängen des Dreiecks.
Mehr lesen, Herons Formel
Wichtige Terminologien des Dreiecks
Die verschiedenen Terminologien im Zusammenhang mit dem spitzwinkligen Dreieck sind:
Rund um die Mitte
Der Mittelpunkt des Kreises, der durch die drei Eckpunkte des Dreiecks verläuft, wird Umkreismittelpunkt des Dreiecks genannt. Sie wird berechnet, indem der Schnittpunkt der Mittelsenkrechten genommen wird. Bei einem spitzwinkligen Dreieck liegt der Umkreismittelpunkt immer innerhalb des Dreiecks.
Im zentrum
Der Mittelpunkt des Kreises, der die drei Seiten des Dreiecks berührt, wird als Mittelpunkt des Dreiecks bezeichnet. Sie wird berechnet, indem der Schnittpunkt der Winkelhalbierenden genommen wird. Bei einem spitzwinkligen Dreieck liegt der Mittelpunkt immer innerhalb des Dreiecks.
Schwerpunkt
Der Schnittpunkt der Mediane eines Dreiecks wird als Schwerpunkt des Dreiecks bezeichnet. Bei einem spitzwinkligen Dreieck liegt der Schwerpunkt des Dreiecks immer innerhalb des Dreiecks.
Orthozentrum
Der Schnittpunkt der Höhe des Dreiecks wird als Orthozentrum des Dreiecks bezeichnet. Bei einem spitzwinkligen Dreieck liegt das Orthozentrum des Dreiecks immer innerhalb des Dreiecks.
Gelöste Beispiele für ein spitzwinkliges Dreieck
Beispiel 1: Welcher der folgenden Winkel kann ein spitzwinkliges Dreieck bilden?
- a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°
Lösung:
Wir wissen, dass alle Winkel im spitzwinkligen Dreieck spitze Winkel sind, das heißt, ihr Maß beträgt weniger als 90 Grad.
Sie folgen auch der Winkelsummeneigenschaft eines Dreiecks, d. h. alle ihre Winkel summieren sich zu 180 Grad.
A) 65°, 75°, 50°
Hier sind alle Winkel spitze Winkel, aber es folgt nicht der Winkelsummeneigenschaft, daher ist das Dreieck nicht möglich.
65°+ 75°+ 50° = 190° (Dreieck nicht möglich)
B) 95°, 40°, 45°
Hier ist das Dreieck möglich, da es der Winkelsummeneigenschaft des Dreiecks folgt, d.h.
95°+ 40°+ 45° = 180
diskrete mathematische NegationAber als wir die Winkel des Dreiecks beobachteten, fanden wir einen stumpfen Winkel von 95°. Daher ist das Dreieck kein spitzes Winkeldreieck.
C) 70°, 40°, 70°
Hier ist das Dreieck möglich, da es der Winkelsummeneigenschaft des Dreiecks folgt, d.h.
70°+ 40°+ 70° = 180
Und als wir die Winkel des Dreiecks betrachteten, stellten wir fest, dass alle Winkel spitze Winkel sind. Daher ist das Dreieck ein spitzes Winkeldreieck.
D) 90°, 45°, 45°
Hier ist das Dreieck möglich, da es der Winkelsummeneigenschaft des Dreiecks folgt, d.h.
90°+ 45°+ 45° = 180
Aber als wir die Winkel des Dreiecks beobachteten, fanden wir einen rechten Winkel von 90°. Daher ist das Dreieck kein spitzes Winkeldreieck.
Beispiel 2: Ermitteln Sie den Umfang eines spitzen Dreiecks XYZ, dessen Seiten XY = 8 Einheiten, YZ = 5 Einheiten und XZ = 9 Einheiten sind.
Lösung:
Gegeben,
Seiten des spitzwinkligen Dreiecks,
- XY(x) = 8 Einheiten
- YZ(y) = 5 Einheiten
- XZ(z) = 9 Einheiten
Wir wissen das,
Umfang des spitzwinkligen Dreiecks (P) = x + y + z
⇒ P = (8 + 5 + 9) Einheiten
⇒ P = 22 Einheiten
Daher beträgt der Umfang des spitzwinkligen Dreiecks 22 Einheiten.
Beispiel 3: Ermitteln Sie die Fläche eines spitzen Dreiecks mit einer Höhe von 12 Einheiten und einer Grundfläche von 15 Einheiten.
Lösung:
Gegeben,
- Höhe des Dreiecks (h) = 12 Einheiten
- Länge der Basis des Dreiecks (b) = 15 Einheiten
Wir wissen das,
Fläche des Dreiecks (A) = ½ × b × h
⇒ A = ½ × 12 × 15
⇒ A = ½ × 180
⇒ A = 90 Quadrateinheiten.
Daher beträgt die Fläche des gegebenen spitzen Dreiecks 90 Quadrateinheiten.
Beispiel 4: Ermitteln Sie die Fläche eines spitzen Dreiecks mit den Seiten AB = 5 cm, BC = 7 cm und AC = 8 cm.
Lösung:
Gegeben,
Seiten des spitzwinkligen Dreiecks,
- AB = c = 5 Einheiten
- BC = a = 7 Einheiten
- AC = b = 8 Einheiten
Wir wissen das,
Fläche des Dreiecks =
⇒ A =
⇒ A =
⇒ A = √(300) cm²
⇒ A = 10√3 cm²
Daher beträgt die Fläche des gegebenen spitzen Dreiecks 10√3 cm².
FAQs zum spitzwinkligen Dreieck
F1: Was sind spitze Winkel?
Antwort:
Der Winkel im Bereich von 0° bis 90° wird als spitzer Winkel bezeichnet. Das heißt, der Minimalwert des spitzen Winkels ist größer als 0° und der Maximalwert des spitzen Winkels ist größer als 90°.
F2: Was ist ein spitzwinkliges Dreieck?
Antwort:
Ein spitzwinkliges Dreieck ist ein Dreieck, bei dem alle drei Innenwinkel spitze Winkel sind, d. h. der Winkelwert liegt zwischen 0° und 90°.
F3: Ist ein gleichseitiges Dreieck immer ein spitzwinkliges Dreieck?
Antwort:
Zeenat Aman Schauspieler
Ja, ein gleichseitiges Dreieck ist immer ein spitzwinkliges Dreieck. Ein spitzwinkliges Dreieck sind die Winkel, bei denen alle Winkel spitze Winkel haben, und im gleichseitigen Dreieck betragen alle Winkel 60°, also spitze Winkel. Daher ist ein gleichseitiges Dreieck immer ein spitzwinkliges Dreieck.
F4: Welche verschiedenen Arten von spitzwinkligen Dreiecken gibt es?
Antwort:
Spitzwinklige Dreiecke werden in drei Typen eingeteilt:
- Akutes Skalenusdreieck
- Gleichschenkliges spitzes Dreieck
- Gleichseitiges spitzes Dreieck
F5: Wie erkennt man, ob ein Dreieck ein spitzwinkliges Dreieck ist?
Antwort:
Ein Dreieck, dessen Innenwinkel kleiner als 90° sind, d. h. alle Innenwinkel sind spitze Winkel, dann wird das Dreieck als spitzwinkliges Dreieck bezeichnet. Wir können überprüfen, ob das Dreieck ein spitzwinkliges Dreieck ist, indem wir einfach die Winkel des Dreiecks beobachten.